这一题在leetcode或者acwing都是有原题的,是比较基础的dp了。
解题思路:对于求最大子矩阵和,我们可以将二维数组进行降维处理,首先外循环枚举出子矩阵的最上面的边i,第二层循环在枚举出子矩阵的最下方的边j,第三层循环枚举出子矩阵的最右边的列k,将二维数组进行降维,变成求一维最大子序列和,然后假设先加上前面的子序列最大和,如果加上去之后子序列最大的和是小于0的,前面的子序列和不能选择,这个列大的子序列的值也不能选,所以将nums这一行的最大子序列置0,继续后面的最大子序列求解。
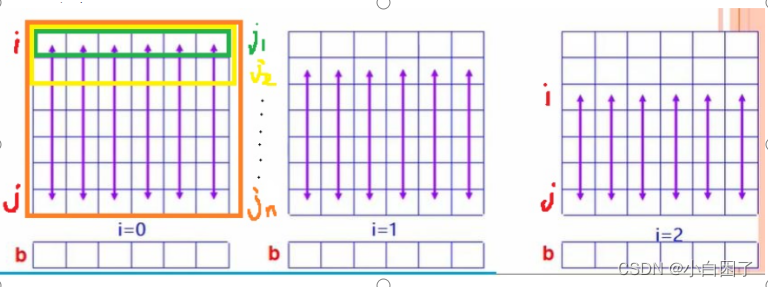
每次枚举起始行和终止行,然后按列求出所有行中该列的总和,然后降维处理,把题目变成求最大的一维子序列和。可以由图得到转移方程:如果tot > 0,tot += sum[k],如果tot <= 0,tot = sum[k];(tot是压缩后第k个序列之前的前缀和)如果maxn小于tot,则将maxn更新为tot;最后输出maxn即为最大子矩阵的和。
代码:
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#include<deque>
typedef long long ll;
typedef pair<ll, ll>PII;
const int N = 5010;
ll n, m;
ll a[N][N];
ll sum[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
ll maxn = 0;
for (int i = 1; i <= n; i++)
{
memset(sum, 0, sizeof sum);
for (int j = i; j <= n; j++)
{
ll tot = 0;
for (int k = 1; k <= m; k++)
{
sum[k] += a[j][k];
if (tot > 0)
{
tot += sum[k];
}
else
{
tot = sum[k];
}
if (tot > maxn)
{
maxn = tot;
}
}
}
}
cout << maxn << ‘\n’;
return 0;
}