文章目录
Misc
Run_it_36_times
题目给了一个pyc文件,反编译试试,得到源代码:
#! /usr/bin/env python 3.6 (3379)
# coding=utf-8
secret = u'You don\u2019t need to restore me to know that the test site is the steganography of pyc.'
def encode(data, encoding='utf-8'):
if isinstance(data, str):
data = data.encode(encoding)
out = [240, 159, 0, 0] * len(data)
for i, b in enumerate(data):
out[4 * i + 2] = (b + 55) // 64 + 143
out[4 * i + 3] = (b + 55) % 64 + 128
return bytes(out)
f = open('hint', 'wb')
f.write(encode(secret))
f.close()
print('See ./hint !')
运行了一下得到一个hint文件,文件内容如下:
??????????????????????????????????????????????????????????????????????????????????????
没看出啥有用的信息,又仔细看了下代码,提示了这道题的考点是pyc文件隐写。那么马上想到剑龙Stegosaurus,直接解密即可。
解密命令:
python .\stegosaurus.py .\Run_it_36_times.pyc -x
这里需要注意一下Python版本,理论上
3.6
以上的都没问题,但实际测试中发现
3.10
的不太行,推荐使用
3.7
的,肯定没问题。

HeiMDall5
是一道压缩包解密题目。
首先给了密码的部分明文,有几位不知道:
_???k?ng_Ctfer
,还给了密码MD5前6位:
1adc88
。
那么首先暴力破解求密码明文:
import string
import hashlib
chars = string.digits+string.ascii_letters
passwd = '_???k?ng_Ctfer'
for a in chars:
for b in chars:
for c in chars:
for d in chars:
p = f'_{a}{b}{c}k{d}ng_Ctfer'
md = hashlib.md5(p.encode()).hexdigest()
if md.startswith('1adc88'):
print(p)
得到密码为
_HaCking_Ctfer
压缩包里有两个文件,使用这个密码只能解压出来rookie.jpg文件。

得到了rookie.jpg的原始文件,那么很明显就是一道考察ZIP压缩包的已知明文攻击题目了。
注意rookie.jpg需要使用同样的压缩算法进行压缩,可以用zip命令进行,使用ARCHPR直接出:

得到压缩包的解压密码
Unkn0wn
解压得到flag:
DASCTF{bc95645ce534a161dd88e75fe98de014}
修猫
给了一个gif图片,发现其中某几帧隐藏了flag字符,直接stegsolve查看即可。
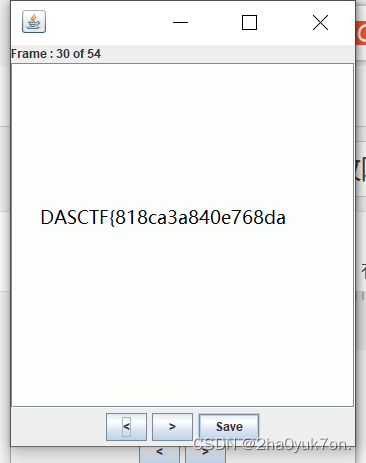
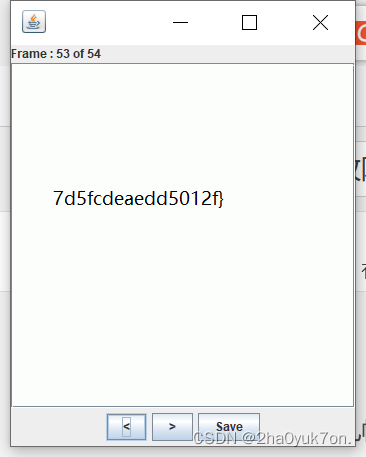
手抄flag:
DASCTF{818ca3a840e768da7d5fcdeaedd5012f}
Crypto
affext
先看源码:
from Crypto.Util.number import *
import random
tables = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789{}'
flag = 'DASCTF{%s}'%("".join(random.sample(tables[:-2], 32)))
tables = "".join(random.sample(tables, len(tables)))
print('tables =', tables)
a = getPrime(6)
b = getPrime(6)
c = ''
for i in range(len(flag)):
c += tables[(a * (len(tables) - 1 - tables.find(flag[i])) + b) % len(tables)]
print('c =', c)
'''
tables = zuSYnb}O1{VoARpPDMgmKwiWZUxde9qNQkL30sTtJvjBH658Er4yhCXafc7G2IlF
c = h17d}vaMUGgNy}ioSD9B8Fvm12qOsXbc6LPzAKQT
'''
开始以为是仿射密码,仔细看又有点不太一样,分析一下,反正都是简单替换密码,每一位的加密字符只和对应位的明文有关。而flag的前7位又是已知的,直接遍历求解
a
和
b
。
from Crypto.Util.number import *
tables = 'zuSYnb}O1{VoARpPDMgmKwiWZUxde9qNQkL30sTtJvjBH658Er4yhCXafc7G2IlF'
ci = 'h17d}vaMUGgNy}ioSD9B8Fvm12qOsXbc6LPzAKQT'
list = sieve_base[:20]
flag = 'DASCTF{'
for a in list:
for b in list:
c = ''
for i in range(7):
c += tables[(a * (len(tables) - 1 - tables.find(flag[i])) + b) % len(tables)]
if c == 'h17d}va':
print(a, b)
# 37 41
得到了a的值为
37
,b的值为
41
这块试了一下用仿射密码解,弄了一会没解出来,但是a和b已经知道了,又是单表代换,就直接爆破吧。
破解脚本:
import gmpy2
tables = 'zuSYnb}O1{VoARpPDMgmKwiWZUxde9qNQkL30sTtJvjBH658Er4yhCXafc7G2IlF'
ci = 'h17d}vaMUGgNy}ioSD9B8Fvm12qOsXbc6LPzAKQT'
a = 37
b = 41
cipher = ''
flag = ''
for i in range(40):
for m in tables:
c = cipher + tables[(a * (len(tables) - 1 - tables.find(m)) + b) % len(tables)]
if c == ci[i]:
print(m, end='')
print(flag)
# DASCTF{aPwVuITibx0dsrkF9AJ5cyXm8o7MhZEK}
easyblock1
先看源码:
from secret import plaintext
class mycrypto:
MIX_C = [[0x2, 0x3, 0x1, 0x1], [0x1, 0x2, 0x3, 0x1], [0x1, 0x1, 0x2, 0x3], [0x3, 0x1, 0x1, 0x2]]
RCon = [0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000, 0x1B000000, 0x36000000]
S_BOX = [[0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76],
[0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0],
[0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15],
[0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75],
[0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84],
[0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF],
[0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8],
[0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2],
[0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73],
[0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB],
[0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79],
[0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08],
[0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A],
[0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E],
[0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF],
[0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]]
def SubBytes(self, State):
return [self.S_BOX[i][j] for i, j in
[(_ >> 4, _ & 0xF) for _ in State]]
def ShiftRows(self, S):
return [S[ 0], S[ 5], S[10], S[15],
S[ 4], S[ 9], S[14], S[ 3],
S[ 8], S[13], S[ 2], S[ 7],
S[12], S[ 1], S[ 6], S[11]]
def MixColumns(self, State):
return self.Matrix_Mul(self.MIX_C, State)
def mod(self, poly, mod = 0b100011011):
while poly.bit_length() > 8:
poly ^= mod << poly.bit_length() - 9
return poly
def mul(self, poly1, poly2):
result = 0
for index in range(poly2.bit_length()):
if poly2 & 1 << index:
result ^= poly1 << index
return result
def Matrix_Mul(self, M1, M2): # M1 = MIX_C M2 = State
M = [0] * 16
for row in range(4):
for col in range(4):
for Round in range(4):
M[row + col*4] ^= self.mul(M1[row][Round], M2[Round+col*4])
M[row + col*4] = self.mod(M[row + col*4])
return M
def encrypt(self, plaintext_list):
State = plaintext_list
for _ in range(10):
State = self.ShiftRows(State)
State = self.MixColumns(State)
State = self.SubBytes(State)
State = self.MixColumns(State)
State = self.ShiftRows(State)
State = self.MixColumns(State)
State = self.SubBytes(State)
State = self.ShiftRows(State)
return State
mycrypto = mycrypto()
ciphertext = mycrypto.encrypt(plaintext)
print(ciphertext)
#[110, 193, 184, 71, 206, 16, 119, 228, 110, 168, 20, 44, 47, 225, 143, 72]
很明显是一道AES的变形,字节代换、行位移都是AES的基本操作,只是分组加密的逻辑没有严格按照AES的算法写。不过没关系,我们逆序推一下就行了。
分别将字节代换、行位移、列混合的函数改写成逆操作,只需要将对应矩阵改写成逆S盒矩阵、位移操作的逆矩阵、列混合的逆矩阵即可。然后是解密函数,将加密函数的操作逆序一遍。
以上如果不太明白的话需要去看一下AES算法的加密原理。AES的原理这里不再赘述,后面有时间的话单独写一篇再讲吧。
解密脚本:
class mycrypto:
IN_MIX_C = [[0xe, 0xb, 0xd, 0x9], [0x9, 0xe, 0xb, 0xd], [0xd, 0x9, 0xe, 0xb], [0xb, 0xd, 0x9, 0xe]]
RCon = [0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000, 0x1B000000, 0x36000000]
IN_S_BOX = [[0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB],
[0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB],
[0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E],
[0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25],
[0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92],
[0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84],
[0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06],
[0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B],
[0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73],
[0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E],
[0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B],
[0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4],
[0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F],
[0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF],
[0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61],
[0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D]]
def InSubBytes(self, State):
return [self.IN_S_BOX[i][j] for i, j in
[(_ >> 4, _ & 0xF) for _ in State]]
def InShiftRows(self, S):
return [S[ 0], S[ 13], S[10], S[7],
S[ 4], S[ 1], S[14], S[ 11],
S[ 8], S[ 5], S[ 2], S[ 15],
S[12], S[ 9], S[ 6], S[ 3]]
def InMixColumns(self, State):
return self.Matrix_Mul(self.IN_MIX_C, State)
def mod(self, poly, mod = 0b100011011):
while poly.bit_length() > 8:
poly ^= mod << poly.bit_length() - 9
return poly
def mul(self, poly1, poly2):
result = 0
for index in range(poly2.bit_length()):
if poly2 & 1 << index:
result ^= poly1 << index
return result
def Matrix_Mul(self, M1, M2):
M = [0] * 16
for row in range(4):
for col in range(4):
for Round in range(4):
M[row + col*4] ^= self.mul(M1[row][Round], M2[Round+col*4])
M[row + col*4] = self.mod(M[row + col*4])
return M
def decrypt(self, ciphertext_list):
State = ciphertext_list
for _ in range(10):
State = self.InShiftRows(State)
State = self.InSubBytes(State)
State = self.InMixColumns(State)
State = self.InShiftRows(State)
State = self.InMixColumns(State)
State = self.InSubBytes(State)
State = self.InMixColumns(State)
State = self.InShiftRows(State)
return State
def printList(lista):
for i in lista:
print(hex(i).replace('0x','').ljust(2,'0'),end='')
print()
mycrypto = mycrypto()
cipher = [110, 193, 184, 71, 206, 16, 119, 228, 110, 168, 20, 44, 47, 225, 143, 72]
plaintext = mycrypto.decrypt(cipher)
printList(plaintext)
# 62b4b4004a796a63915c4d3ed890c500
rrrsssaaa
先看源码:
from Crypto.Util.number import *
from gmpy2 import *
from secret import flag
p = getPrime(512)
q = getPrime(128)
r = getPrime(512)
a = p**3 + q**4
n = p * q * r
e = 65537
m = bytes_to_long(flag)
c = powmod(m,e,n)
print('a =', a)
print('n =', n)
print('c =', c)
'''
a = 1001757897913772351510420195662626456337522550684606727483773096673299029784598925879489541145425035208954548434364407129536623872359866140502945055841821765538135618785958230881698432164666106480484384998915283051445946164568339012311071022667483689786104241205203770248137327154122271358173278768580995401804353335810303663245624828137303106291342454008598042561788843169528260839797410662782024780465758566251328065946252974178694612662193108827812380093012592
n = 19743856964263732842999962921764407899550835757434895392940479421960735302959163991849377985049404173836251900687827441599500422841626517558622567745437335569126719161072741233680254267603047267283814233895186061759120509099394028737117210315668037567644106922178370110286156290354552013641623466808054072066874721501635305497521532247446583415341
c = 11573369450591319755076158585550356804136715495771905025393681593171072453674223539740220735995000501270745453812328856003963738281166754397539243769043057759237596024541470868109828449256053991918612982581009998827964614610819962346527488888094333196535012014776795315145414671509148454534127080694322513052946539505422338224596999797852421340273
'''
考察RSA的题目,开始一直想着用已知定理去推导,后来仔细一看,p和q相差过大,直接开三次方求p即可。下面就是RSA常规解法了,解密脚本:
import gmpy2
import libnum
e = 65537
a = 1001757897913772351510420195662626456337522550684606727483773096673299029784598925879489541145425035208954548434364407129536623872359866140502945055841821765538135618785958230881698432164666106480484384998915283051445946164568339012311071022667483689786104241205203770248137327154122271358173278768580995401804353335810303663245624828137303106291342454008598042561788843169528260839797410662782024780465758566251328065946252974178694612662193108827812380093012592
n = 19743856964263732842999962921764407899550835757434895392940479421960735302959163991849377985049404173836251900687827441599500422841626517558622567745437335569126719161072741233680254267603047267283814233895186061759120509099394028737117210315668037567644106922178370110286156290354552013641623466808054072066874721501635305497521532247446583415341
c = 11573369450591319755076158585550356804136715495771905025393681593171072453674223539740220735995000501270745453812328856003963738281166754397539243769043057759237596024541470868109828449256053991918612982581009998827964614610819962346527488888094333196535012014776795315145414671509148454534127080694322513052946539505422338224596999797852421340273
p = gmpy2.iroot(a,3)[0]
q = gmpy2.iroot(a-p**3,4)[0]
r = n//p//q
phi = (p-1) * (q-1) * (r-1)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c, d, n)
print(libnum.n2s(int(m)))
# DASCTF{0c3a5a81d477e119900e84620055c128}
Reverse
babyencrypt
查壳看到使用
Pyinstaller
打包:
反编译为pyc文件,然后再反编译为py文件,这里还涉及一个pyc文件修复。
直接反编译pyc文件是不成功的,看下文件头,前几个字节代表Python版本:
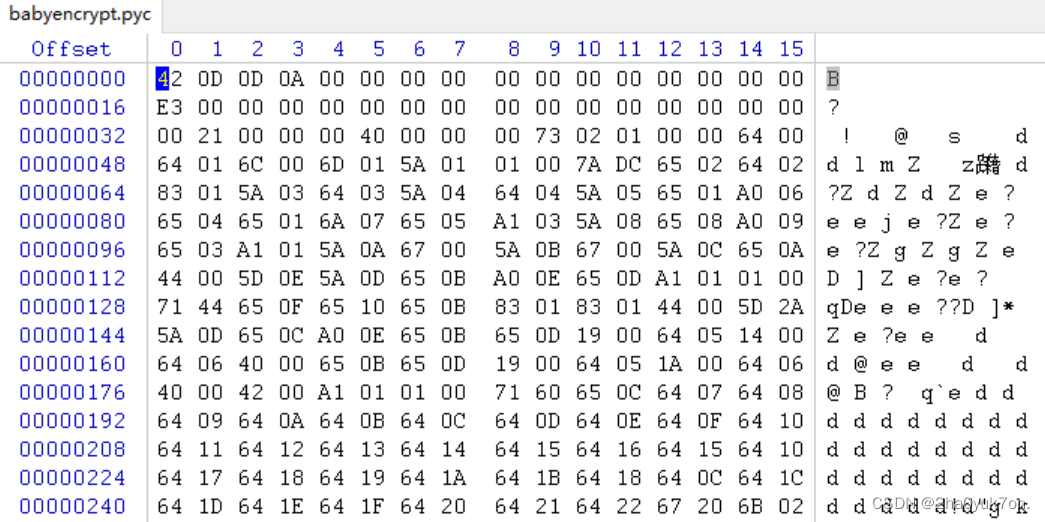
对比一下struct.pyc文件头,将前16个字节修改一致。

修改完pyc文件头后进行反编译,成功得到py源文件:
from Crypto.Cipher import AES
try:
flag = input('plz input your flag:')
key = '6666wjldasctfcom'
iv = 'comdasctfwjl6666'
ci = AES.new(key, AES.MODE_CBC, iv)
c = ci.encrypt(flag)
xx = []
xxx = []
for i in c:
xx.append(i)
else:
for i in range(len(xx)):
xxx.append(xx[i] * 16 & 255 | xx[i] // 16 & 255)
else:
if xxx == [90, 250, 163, 52, 109, 122, 36, 214, 77, 227, 240, 216, 173, 95, 20, 194, 20, 227, 54, 32, 161, 65, 124, 32, 122, 212, 46, 42, 82, 254, 112, 233]:
print('pass')
else:
print('error')
except:
print('error')
分析后看到是一个AES加密,并且对加密结果进行了一定变换。整理一下思路,编写解密脚本,这里不需要逆推加密逻辑,直接暴力破解即可:
from Crypto.Cipher import AES
xxx = [90, 250, 163, 52, 109, 122, 36, 214, 77, 227, 240, 216, 173, 95, 20, 194, 20, 227, 54, 32, 161, 65, 124, 32, 122, 212, 46, 42, 82, 254, 112, 233]
key = b'6666wjldasctfcom'
iv = b'comdasctfwjl6666'
ci = AES.new(key, AES.MODE_CBC, iv)
list = []
for a in xxx:
for b in range(300):
d = b * 16 & 255 | b // 16 & 255
if d == a:
list.append(b)
break
m = ci.decrypt(bytes(list))
print(m)
# DASCTF{r3verse_aes_1s_comm2n!!!}
just try
反编译定位到加密代码:
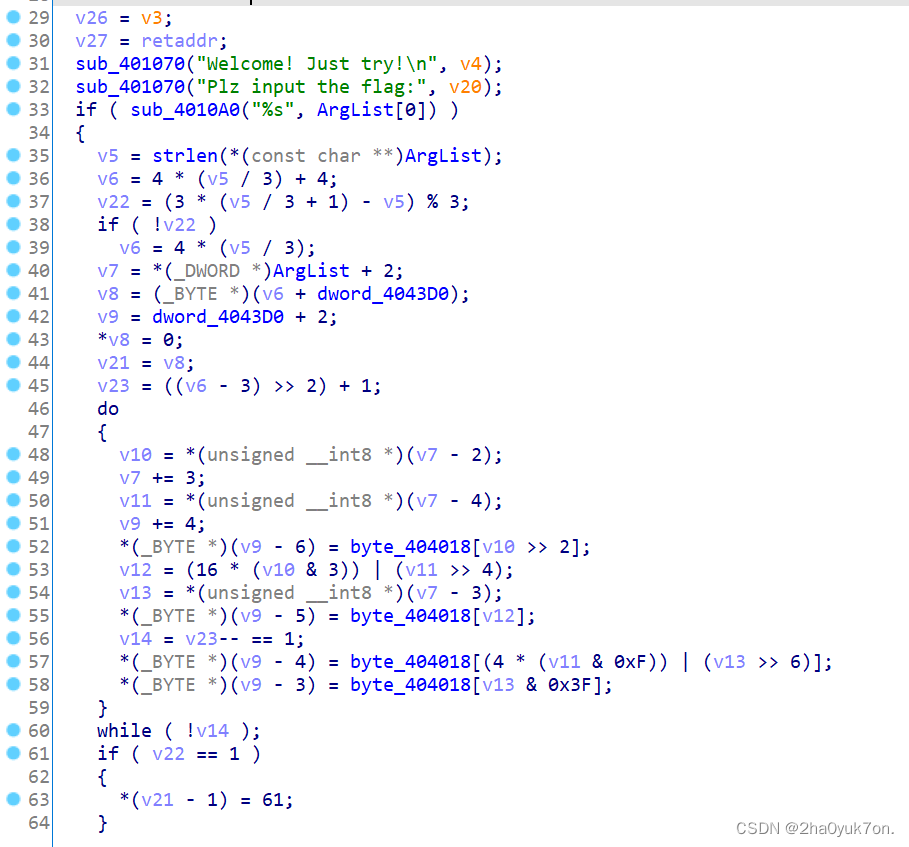
加密逻辑为:
#include <stdio.h>
const char* bytes = "pc$LEQz=`J&x}Z1H[_#WY?7(d+beh9Rg%U.omaADIn/^r2qj\"X8*SPiVT~,!@0lO";
void encode(char* src)
{
size_t len = strlen(src);
size_t bufsize = 4 * (len / 3) + 4;
size_t padding = (3 * (len / 3 + 1) - len) % 3; // len % 3;
if (!padding) {
bufsize = 4 * (len / 3);
}
char* buf = (char*)malloc((bufsize + 1) * sizeof(char));
char* pSrcStart = src + 2;
char* pBufEnd = bufsize + buf;
char* pBufStart = buf + 2;
*pBufEnd = 0; // 结尾反杠零
size_t i = ((bufsize - 3) >> 2) + 1; //循环计数
do {
char c1 = *(pSrcStart - 2);
pSrcStart += 3;
char c2 = *(pSrcStart - 4);
pBufStart += 4;
*(pBufStart - 6) = bytes[c1 >> 2]; // 标注(1)
int v9 = 0x10 * (c1 & 0x3) | (c2 >> 4); // 标注(2)
char c3 = *(pSrcStart - 3);
*(pBufStart - 5) = bytes[v9]; // 标注(3)
*(pBufStart - 4) = bytes[4 * (c2 & 0xF) | (c3 >> 6)]; // 标注(4)
*(pBufStart - 3) = bytes[c3 & 0x3F]; // 标注(5)
} while (i-- != 1);
if (padding == 1) {
*(pBufEnd - 1) = '=';
}
else if (padding == 2) {
*(pBufEnd - 1) = '=';
*(pBufEnd - 2) = '=';
}
printf("%s", buf);
free(buf);
}
int main()
{
encode("abcddd");
return 0;
}
下面的思路是分析静态加密代码,写脚本暴力破解然后动态调试,这里参考了一篇文章,直接贴原文章吧,链接如下: