堆排序——topk问题

用内置的sort()函数排序,时间复杂度为O(nlogn),实际上还需加上切片的步骤k,但由于k<n,可以省略。


将列表前5个元素取出来,建立一个小根堆,堆顶的1目前是第5大的数。

接着取后面的元素0,0比1小故忽略,继续取元素7,7比1大,用7替换堆顶元素1,并且对堆进行向下调整。

继续取剩下的4和5,替换堆顶元素并调整,最终倒序弹出堆顶就得到topk的值。

topk问题代码实现:
def sift(li, low, high): # 向下调整为小根堆,改变一下if语句判断符号即可
i = low
j = 2 * i + 1
tmp = li[low]
while j <= high:
if j + 1 <= high and li[j+1] < li[j]: # 如果右孩子有并且比较小
j = j + 1 # j指向右孩子
if li[j] < tmp:
li[i] = li[j]
i = j # 往下看一层
j = 2 * i + 1
else: # tmp更小,结束循环
break
li[i] = tmp # 每次把较小的提上根节点后,将tmp放到对应的孩子结点
def topk(li, k):
heap = li[0:k]
for i in range((k-2)//2, -1, -1):
sift(heap, i, k-1)
# 1.建堆
for i in range(k, len(li)-1):
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k-1)
# 2.遍历
for i in range(k-1, -1, -1):
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i - 1)
# 3.出数
return heap
import random
li = list(range(1000))
random.shuffle(li)
print(topk(li, 10))
归并排序——归并

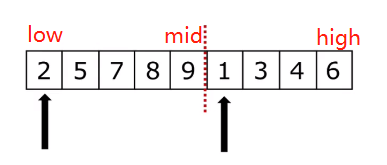
比较low和mid+1位置的两个数大小,将较小的1取出,放到临时创建的列表,指针往后移一位,变成mid+2,当有一侧元素已被全部取出,将剩下的有序列表全部放到临时列表后面。
def merge(li, low, mid, high):
i = low
j = mid + 1
ltmp = []
while i<=mid and j<=high: # 只要左右两边都有数
if li[i] < li[j]:
ltmp.append(li[i])
i += 1
else:
ltmp.append(li[j])
j += 1
# while执行完,肯定有一部分没数了
while i <= mid:
ltmp.append(li[i])
i += 1
while j <= high:
ltmp.append(li[j])
j += 1
li[low:high+1] = ltmp
# li = [2,4,5,7,1,3,6,8]
# merge(li, 0, 3, 7)
# print(li)
归并排序——使用归并


归并排序代码实现:
def merge_sort(li, low, high):
if low < high: #至少有两个元素,递归
mid = (low + high) //2
merge_sort(li, low, mid)
merge_sort(li, mid+1, high)
merge(li, low, mid, high)
li = list(range(1000))
import random
random.shuffle(li)
print(li)
merge_sort(li, 0, len(li)-1)
print(li)
归并排序复杂度
每次归并时间复杂度为O(n),总共有logn次归并,故归并排序的时间复杂度为O(nlogn)。
归并排序与之前的排序不一样的地方在于,它需要生成一个额外的列表存储数据,空间复杂度为O(n)。而之前的排序都是原地排序,通过交换等操作存储数据,不需要额外的存储空间。
python内置的sort方法内部实现其实就是基于归并排序算法。
NB三人组小结


快速排序空间复杂度不是O(1)怎么理解呢?递归需要用到系统栈的空间,函数要往下一层一层地走,存储函数也需要空间,每一层占用的空间为O(1),快排平均经过logn次递归,空间复杂度为O(logn);最坏的情况要经过n次递归,故空间复杂度为O(n)。
排序算法的稳定性是指:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
举个例子,对’name’进行排序:
# 原来的序列
{'name':'a','age':18}
{'name':'b','age':20}
{'name':'a','age':25}
# 稳定的排序
{'name':'a','age':18}
{'name':'a','age':25}
{'name':'b','age':20}
# 不稳定的排序
{'name':'a','age':25}
{'name':'a','age':18}
{'name':'b','age':20}
简单来说,有顺序挨个换的都是稳定的排序,飞着换的都是不稳定的排序。
怎么理解呢,拿冒泡排序举例,就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,我想你是不会再无聊地把他们俩交换一下的,所以挨个交换的是稳定的排序。
用选择排序举个例子,序列5 8 5 2 9, 我们知道第一遍选择第1个元素5会和最小的元素2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法,应为它的比较交换不是在相邻两个元素间进行的。
堆排序父节点和孩子节点在列表中的存储位置是不相邻的,故堆排序也是不稳定的排序。