目录
序言
如果信号沿着传输线传播时，感应到的瞬态阻抗发生变化（阻抗不连续或不匹配），就会导致一部分信号能量被反射，另一部分信号产生失真后继续传播，反射
和失真会使到达终端的信号质量变
差，这一原理就是大多数信号完整性问题产生的根源（不包含串扰等复杂耦合问题），
最常见的现象
是信号振铃
，如下图所示，振铃就是由于终端阻抗不匹配和多次反射而产生的。
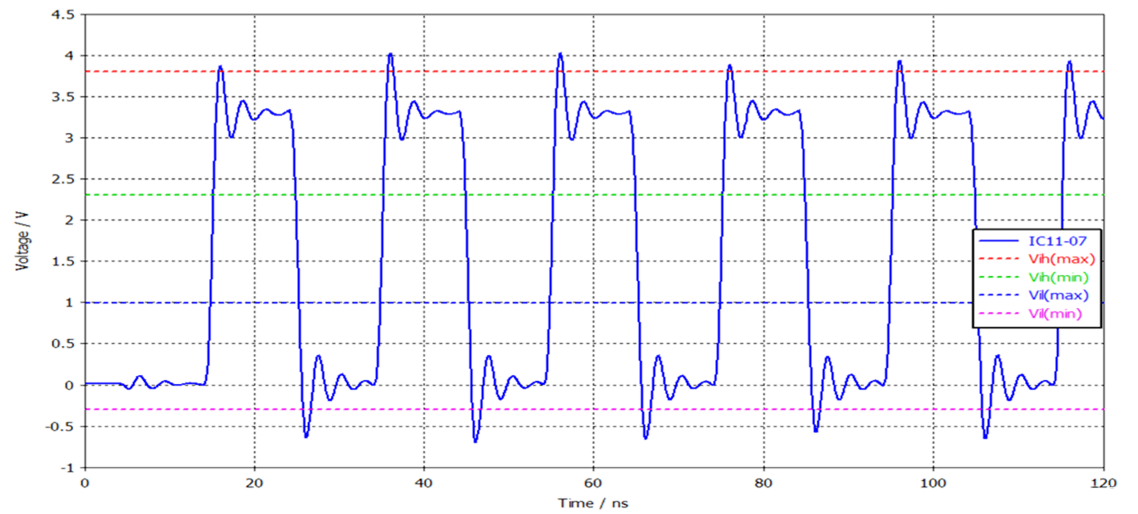
除终端外，阻抗不连续所导致的反射可能发生在传输线结构的任一环节，比如过孔、分支、拐角、焊盘、接插件等等，采取的优化措施可能包括：圆弧走线、增大反焊盘尺寸、禁止非功能焊盘、挖空参考面、带状线布线、控制阻抗、约束走线长度等等
，归根到底，传输线的最终设计目标，其实就是尽可能地保证信号感应到的阻抗连续性。
反射系数
开始讨论具体问题之前，需要了解什么是反射系数？
用一个简单的例子来进行解释，如下图所示，描述了信号经过一个长度为
𝑙
的
传输线传播后，负载
𝑅
𝐿
处的入射及反射电压电流的情况，根据基尔霍夫定律，可以得出流过负载
𝑅
𝐿
的电压及电流的表达式如下；
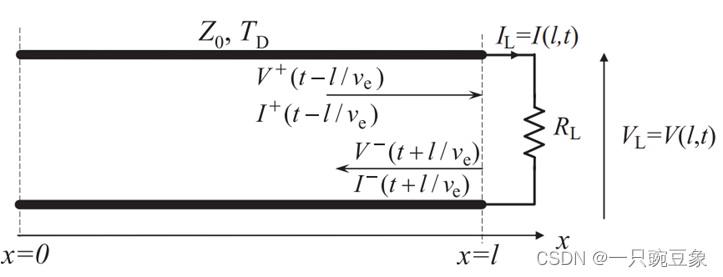
其中，
表示以传播速度
𝑣
𝑒
沿
+x方向前进的波，
表示以传播速度
𝑣
𝑒
沿
-x
方向返回的波；
负载的反射系数可以等效为反射电压与入射电压的比例关系，并且带入公式1、2
联立求解可以得到如下关系式：
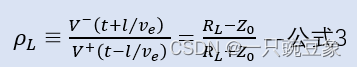
根据公式3
可知，
反射系数的取值范围为
-1≤
𝜌
𝐿
≤1
：
1）
𝑅𝐿
= 0
，
𝜌
𝐿
=−1
，相当于负载短路，此时，注入波会发生全负反射；
2）
𝑅𝐿
=
𝑍0
，
𝜌
𝐿
=0
，相当于负载匹配，此时，注入波不会发生反射；
3）
𝑅
𝐿
=
∞
，
𝜌
𝐿
=
1
，相当于负载开路，此时，注入波会发生全正反射。
同样的道理，当反射波到达源端时，同样也会由于阻抗的失配产生源端的反射，因此，源端也存在反射系数，并且如公式
4
所
示：
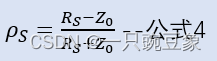
根据反射系数，可以计算出任意阻抗的反射信号，当端接阻抗是电阻元件时，阻抗为常数，很容易求得反射电压，当端接是较为复杂的阻抗特性时，如容性、感性或者组合
，手工计算就会非常困难，需要借助电路仿真工具，接下来，所讨论的都是基于电阻端接的情况。
信号上升时间与传播时延
以一个简单的例子来直观地解释这个问题，如下图所示，利用
CST
软件设计一个简单的微带传输线模型，参数如下：
1）信号源：0~2V
变化的阶跃信号，源内阻为
10ohm
；
2）传输线：特性阻抗100ohm
，相对介电常数
𝜀
𝑟
=4
（对应
传播速率为
150mm/ns
），线长
750mm
，则对应的传播时延为
𝑡
𝑑
=5
𝑛𝑠
；
3）负载：1Mohm
负载电阻值；
分别用具备不同的上升沿时间
𝑡
𝑟
的信号源作为激励，再通过观察输入和输出信号的变化情况，以研究上升时间与传播时延之间的比例关系对信号
失真度（反射）的
影响。
仿真的结果如下图所示：
1）
𝑡𝑟=0.2
𝑡
𝑑
，相当于
信号上升沿时间很短，会很快地达到稳定电平的输出状态，输出稳定后会发现，输入和输出的信号电压均会出现明显的台阶，并且每个状态的
持续时间
≈
2
𝑡
𝑑
，
这是因为入射信号在达到稳态后，还有充足的时间达到反射电压的最大值，然后送回到源端，并且停留的
时间近乎等于
信号传播时延的两倍，即前一个反射电压会维持到到下一个反射状态的到来而更新；
2）
𝑡𝑟
=2
𝑡
𝑑
，
此时，依然
满足源端反射电压达到
最大值的条件，但是，其达到稳定电平的时间会因为上升沿的变缓而变
长，即反射电压停留的时间被挤压，
所以，反射的
信号
电压
刚
到达源端即被下一个反射状态的到来而更新掉；
3）
𝑡𝑟
=4
𝑡
𝑑
，
此时，上升沿时间已经足够缓慢，达到稳定电平输出的时间非常长，反射的电压状态根本没有时间完成一个完整的反射过程即被下一个状态所覆盖，因此，看起来，输出和输入电压波形发生反射失真
的现象并不明显，输出
波形更加贴近于输入
波形，此时，就称为信号的失真度降低。
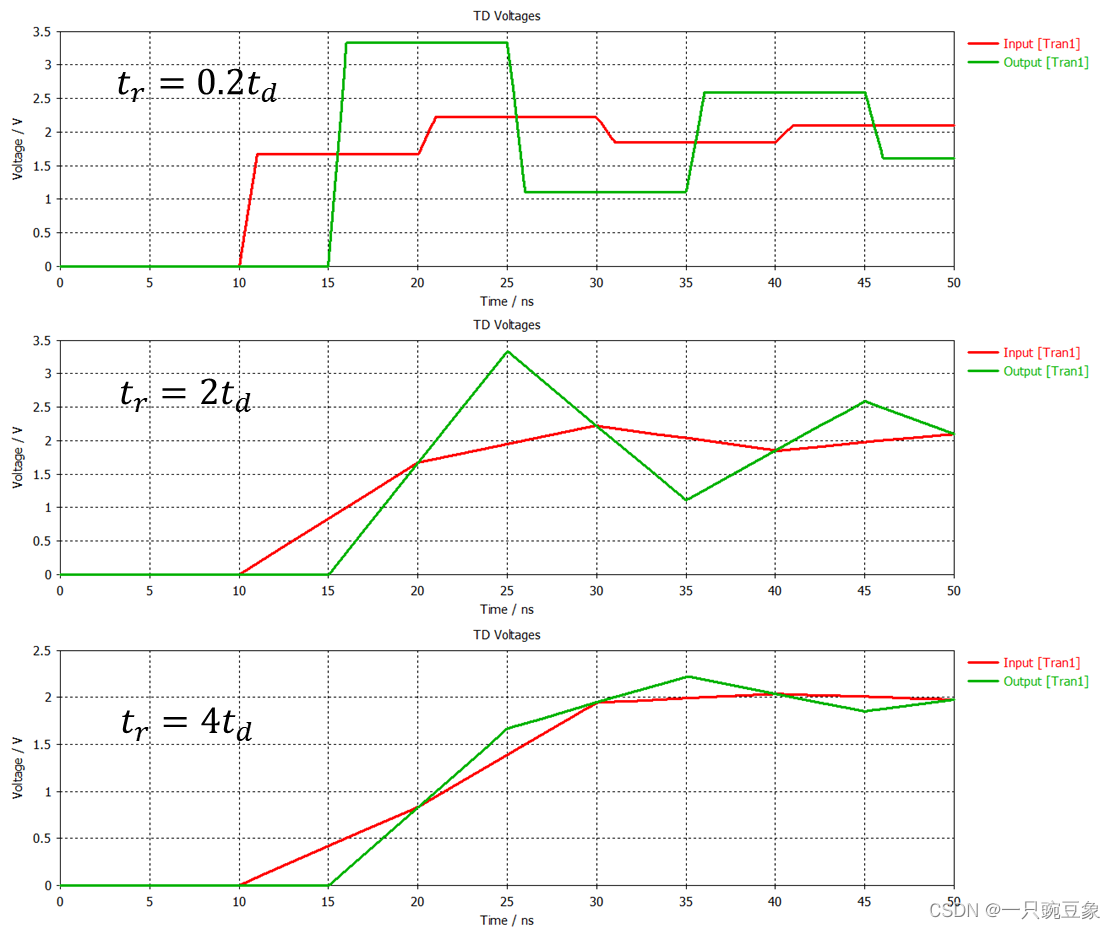
因此，对于设计者来说，信号的上升沿时间越缓慢、传输线长度越短，越不容易产生严重的信号完整性问题，但这又是与高速信号的设计理念相违背的，因此，设计中的反射问题是不可避免的。
这些对仿真结果的描述，对于大多数不甚了解反射过程的读者还是略显晦涩，但对于它的理解，却对如何分析传输线上产生的各种变化又至关重要，其实，只要谨记
𝑡
𝑟
≪
2
𝑡
𝑑
这个关系，那么你的设计就需要对信号质量进行严格地管控，因为此时，正如上文
𝑡
𝑟
=0.2
𝑡
𝑑
的情况相同，每个反射电压的状态都可能被完整地体现在你的设计线路的波形测量上。
换个说法，通过手工计算的方式，我们可以得到所有的源端和终端的电压状态，但
这些
状态
只有
在
𝑡
𝑟
≪ 2
𝑡
𝑑
时，才可能在你的设计
中得到完整的体现。
电压反弹图计算模型
反射过程需要花时间去理解，但是，反射电压的计算，却是动手立即可以做到的。
任一节点的电压代数和为
U=U
0
+U
入射电压
+U
反射电压
，整个的电压反射计算过程如下图所示：
如上图所示，已知源电压是U0
，输入到传输线上的电压相当于源内阻和传输线特性阻抗的分压，即
Us1
，当其传输到负载端时，由于存在反射系数
𝜌
𝐿
，
在负载端产生的电压是入射电压
Ua
、产生的反射电压
Ub
之和，反射电压
Ub
会继续返回到源端，由于存在反射系数
𝜌
𝑆
，
Ub
将被作为源端的入射电压而产生新的反射电压，因此，第二次在源端产生的电压是已存在的源电压
Us1
、新入射电压
Ub
、新反射电压
Uc
之和，以此类推，后面的反射过程就是以上过程的重复。
在工程上，经常用这个简单的电压反弹图来预估传输线上的电压走势。
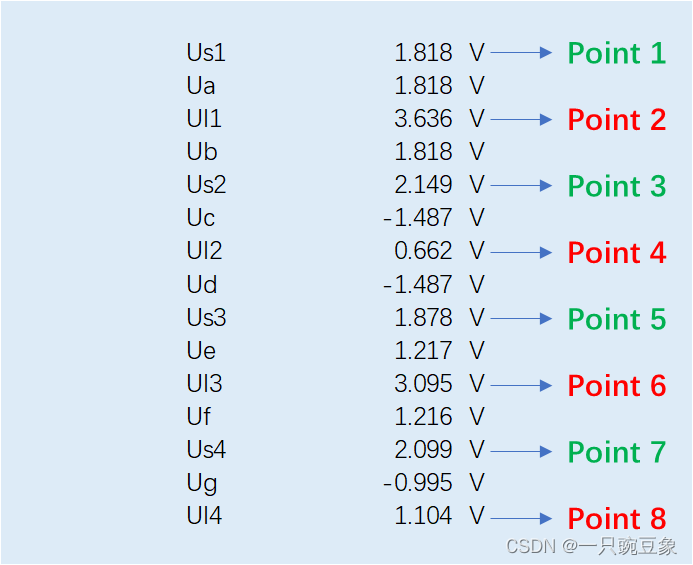
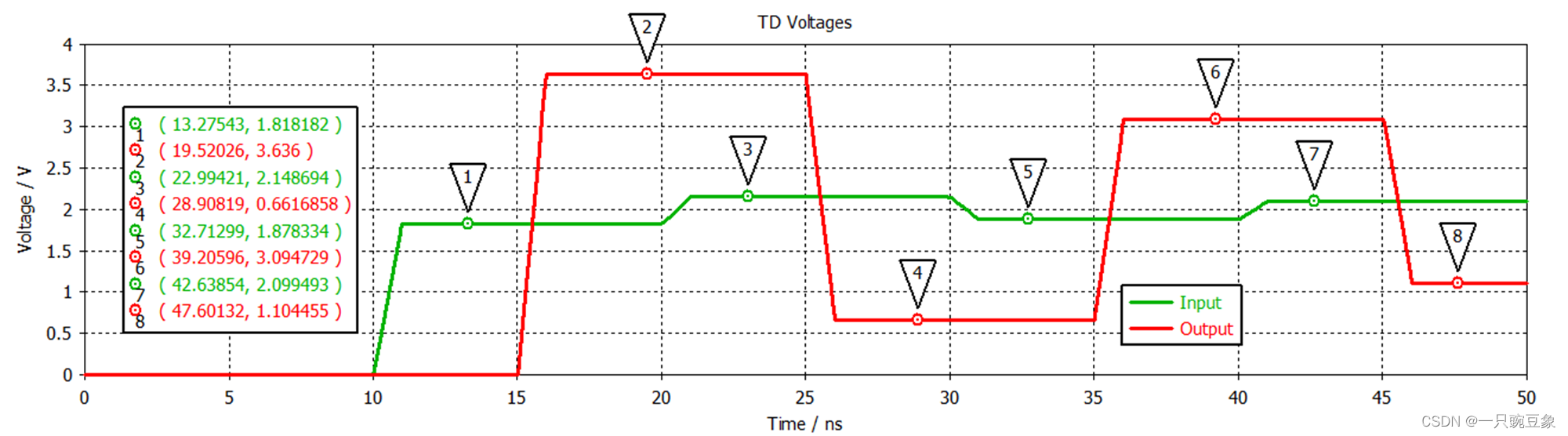
按照上述的过程，可以计算如下图所示的该传输线例子中的源端以及负载端的各个反射阶段的电压
值，
并与
CST
电路仿真软件的计算结果（
𝑡
𝑟
=0.2
𝑡
𝑑
时）进行了对比，发现两者完全一致。
时域反射
–TDR
除了通过计算及仿真传输线电路获取电压波形外，还可以使用称为时域反射计—TDR
的方式来测量及仿真反射波形，不同之处在于，
TDR
往往表征的是传输线阻抗而非电压在时域中的表现形式，因此，其显示的结果将更为直观地告诉设计师传输线的阻抗控制
情况，但是由于专用的
TDR
工具非常的昂贵，一般的设计公司是没有的，这种情况下，
TDR
仿真就是一个不错的选择。
理解TDR
工作原理的一个关键点，依然是要清楚
做为脉冲激励源信号
的上升沿时间的选择，再举一个简单的微带传输线的例子，可能更有助于大家的领悟：使用两段特性阻抗为
75ohm
，长度为
150mm
的传输线进行级联，中间接入一段特性阻抗为
75ohm
，长度
为
5
mm
的开路分支，考察下
不同上升沿时间的
激励
源注入
下，开路
分支给传输线所
带来的阻抗波动情况。
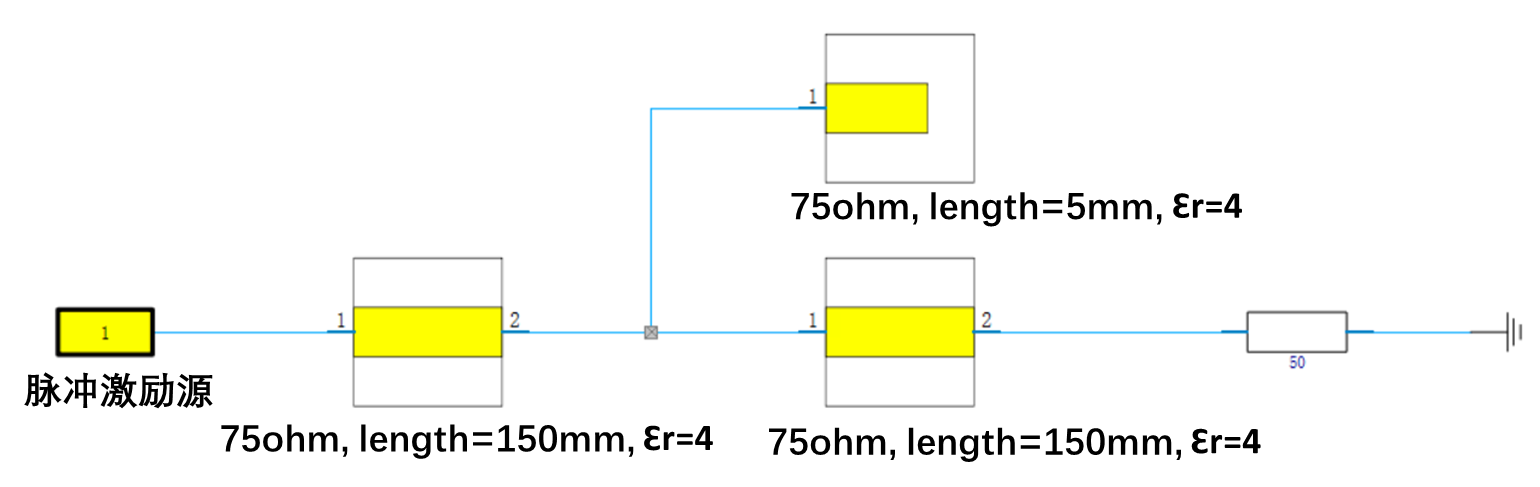
TDR
激励源的设置
实际测量中，一个上升的矩形脉冲做为激励信号是TDR
评估的典型脉冲，但是，它的缺点是能量不会衰减（电平稳定后不会随时间而变化），因而容易引入不必要的
信号反射振幅
，当用高斯脉冲激励时，这个缺点则不会出现，因此，仿真中，经常使用高斯脉冲做为激励信号；
如下图所示，高斯脉冲的能量主要集中于其上升和下降沿，这种情况下，上升时间与频段的上限相关，在CST
软件中，上升时间被定义为
10%~90%
的边沿时间，频率范围则调整为
0~
𝑓
𝑚𝑎𝑥
，
其采用的比例
关系
如公式
5
所示
，
如果上升沿是
35ps
，则对应
的仿真信号带宽就需要设置为
0.876/35ps
= 25.14GHz
：
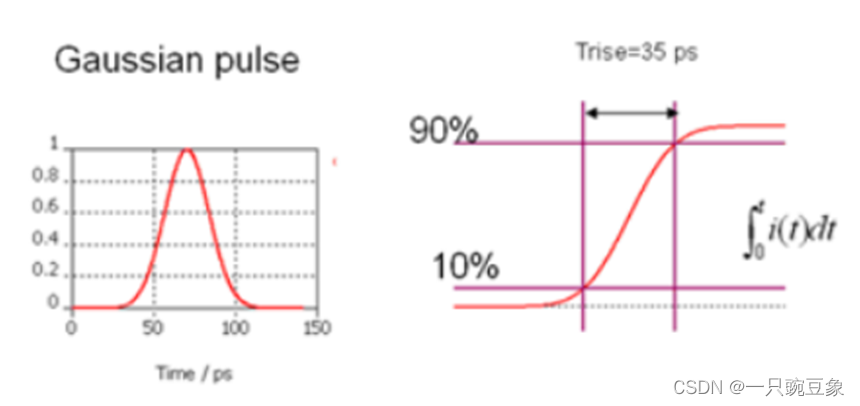
需要注意，不同的仿真软件，这个比例关系是不同的，比如
ADS
，这个值就变为
0.75
，
具体可以参考对应软件的帮助
手册
，另外，做一个预告，后续，小编将写一篇文章，专门讨论下上升沿时间和带宽的关系，敬请期待！！！
走线分支的影响评估
说到走线分支，很多小伙伴肯定不陌生，但是，到底该如何对其进行有效评估，估计已经困惑了很久，所以，在开始正式的仿真之前，需要以一个合理的理论评估做为设计支撑，本文，将分支看成一段终端开路的传输线，假设一个正弦波信号从左端口注入（即传输线上的分叉结点处），沿着分支进行传播，如果传输长度
=1/4
正弦波工作波长时，那么当注入波在分支的底部反射
并
再次
到达
结点处时，反射信号正好延迟了
1/2
个周期，即信号产生了
180
度的相位差，这种情况下，前一
个
正弦
波峰
产生的反射
电压将
与下一
个
正弦
波谷
的电压在结点处叠加，并且相位反相，信号电压可能被完全抵消掉
。
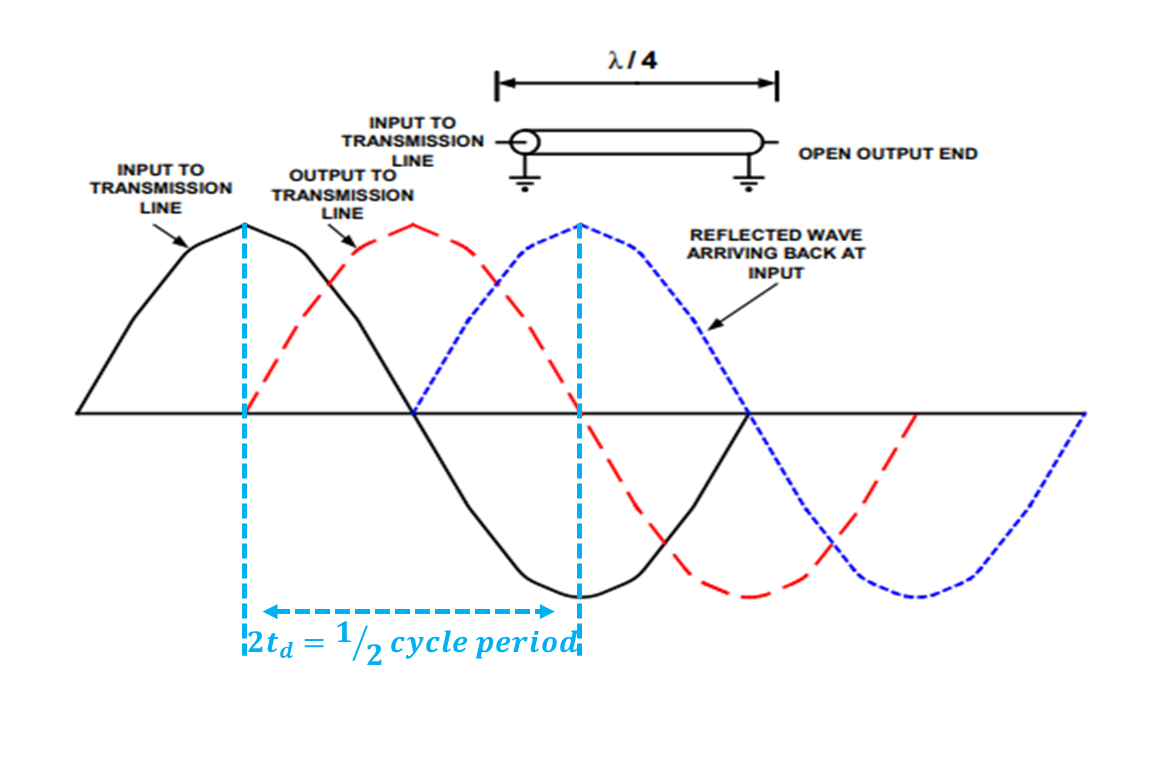
值得强调
的一点，因为正弦波信号是没有信号平顶的，因此，其工作频率等于基频，此时，可以近似看成是
𝑡
𝑟
=2
𝑡
𝑑
（这里，就解释了前文反射环节中所讨论的这个临界点的含义所在，当成一个彩蛋，如果真的认真读到了这个地方，相信也可以增强理解了，哈哈），而实际设计中，传输线上搭载的往往是各种方波信号，其变化的前后沿会带来丰富的高次谐波，因此，其工作波长应当等于设计所关注的最高工作频率，而不是信号基频，所以，
𝑡
𝑟
=2
𝑡
𝑑
这个关系将会变成
𝑡
𝑟
≪
2
𝑡
𝑑
，这点请谨记！！！
TDR仿真分析
有了上述的关于反射和分支的理论支撑后，相信接下来的分析过程将会变得更加简单：
紧接上一个电路设计，5mm分支的信号传播时延
𝑡
𝑑
为
33.33ps
，假设这段传输线用于传输
4Gbps
的
NRZ
码，则其传输带宽为
2GHz
，通常系统带宽会考虑到
10GHz
，则其满足分支最坏影响的传播延时为
25ps
，已经非常接近实际时延值，设计时需要格外关注
；
根据公式
5
，仿真中，
10GHz
对应
的激励
源上升沿时间
=
0.876/10GHz=87.6p
s
；
设计中采用了相同的介电常数
𝜀
𝑟
=4
（对应
传播速率
150mm/ns
），所以，两段
150mm
微带线总的传播时延为
2ns
，因为激励源时间为
87.6ps
，总的仿真预估时间
=2*(2ns+87.6ps)=4.1752ns
，那么，仿真时间设置到
5ns
即可；
为了方便结果对比，这里选取TDR
仿真激励源带宽分别为
30G
、
1
0G
、
5G
、
1
G
四
种情形，其对应的信号上升沿分别为
29.2ps
、
87.6ps
、
175.2ps
、
876ps
，仿真结果如下图所示，通过结果对比可以发现，随着激励源带宽的提升，上升沿的变小，由分支所带来的反射现象将愈发明显，并且，在
10GHz
时，该分支造成的阻抗波动已经非常严重了（如蓝色实线所示），这也符合小编对它的设计预估，因此，当分支在设计中不可避免时，设计者就需要明确知道
该系统的运行带宽的上限或最快的信号上升沿时间，才可以做出合理的判断。
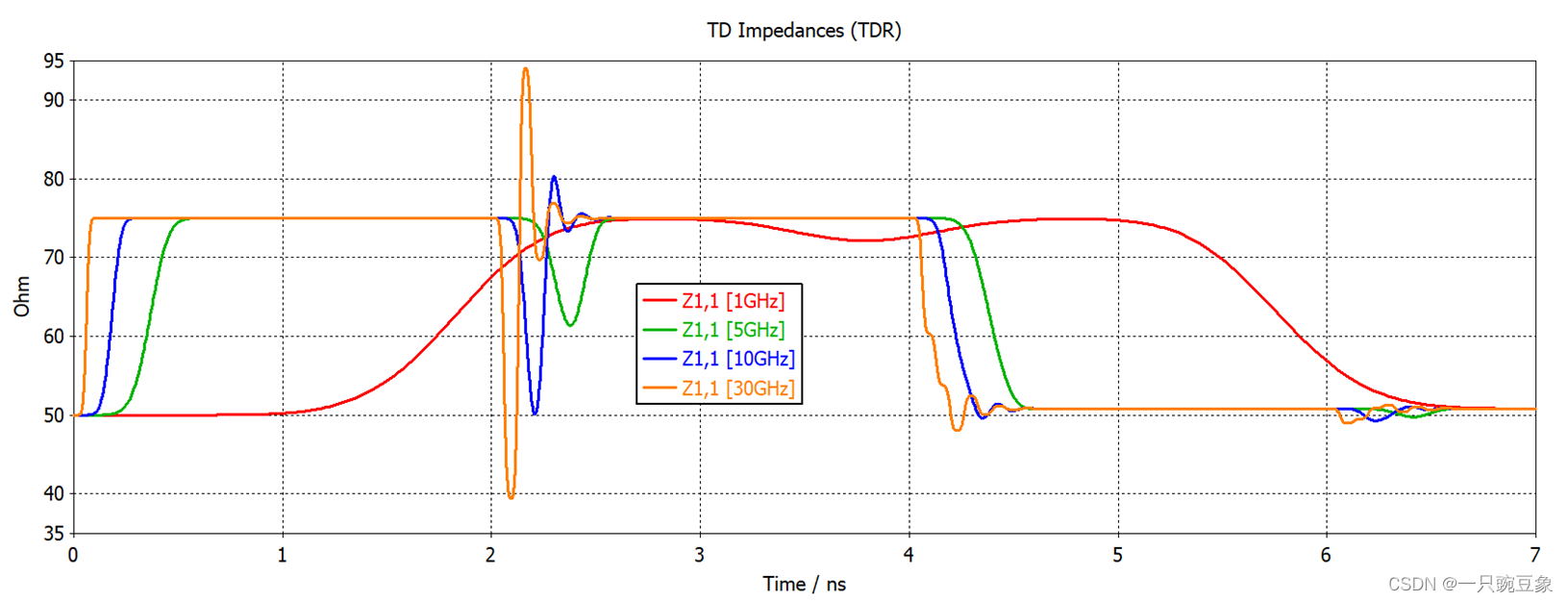
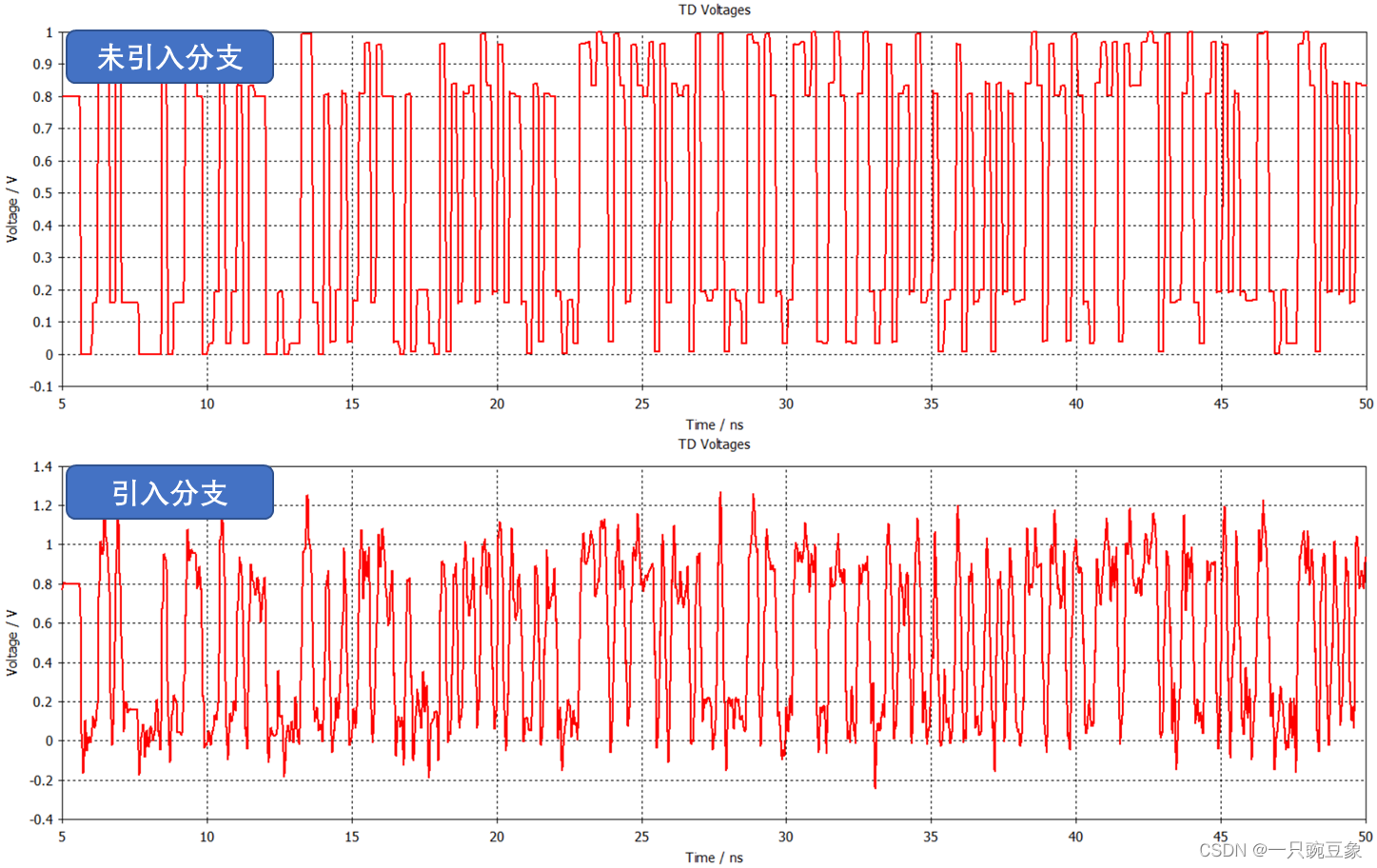
通过TDR
的结果，知道信号会感应出严重的阻抗不连续，再来观察下时域波形的表现情况，如下图所示，当不引入分支时，负载端的时域电压波形仅会因为阻抗失配带来电压幅度的波动，并未对前后沿造成干扰，但是，当引入分支后，由于分支的传播延时已经与临界设计值相接近，带来了强烈的信号反射，从而导致了严重的信号失真问题，由于不同相位电压叠加的原因，时域波形的信号边沿以及幅度均遭到了严重的削减。
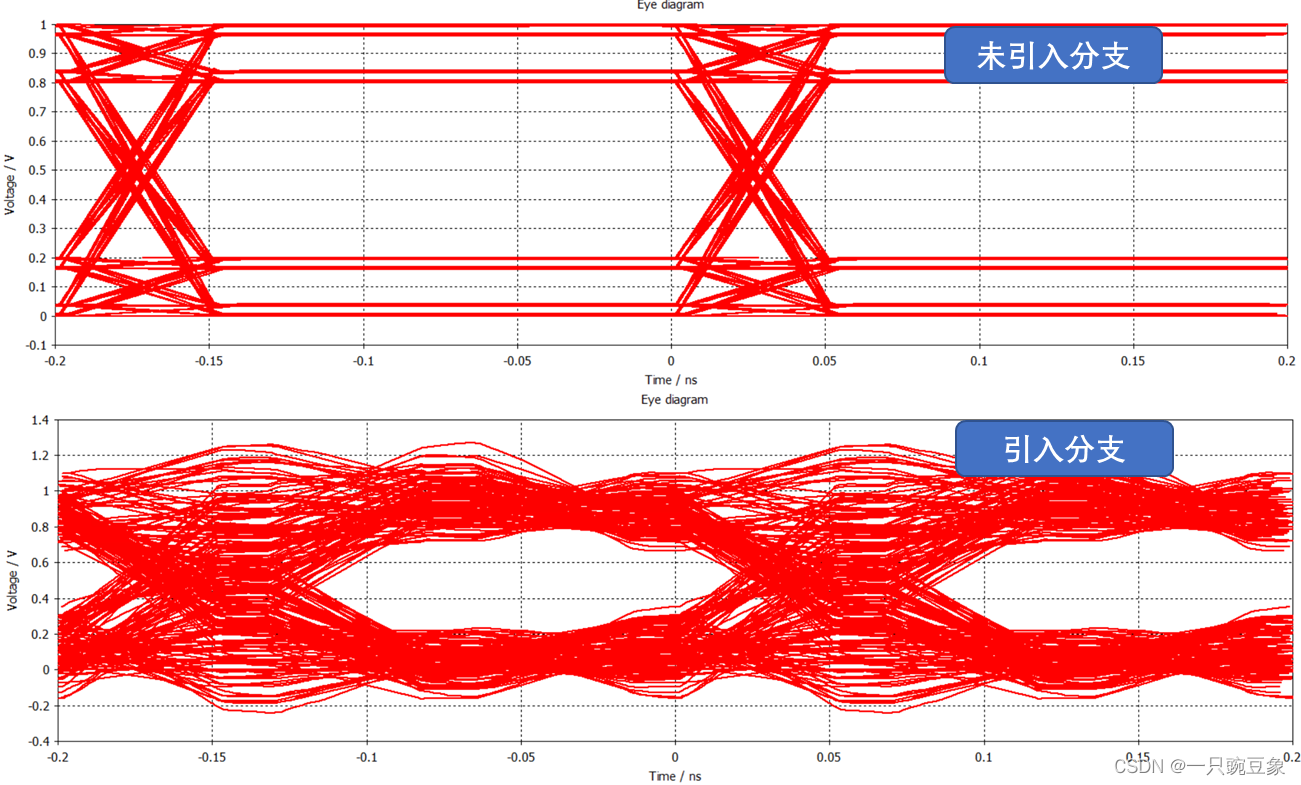
将上述时域信号进行叠加形成眼图，可以更为直观地看出分支引入前后对信号产生的影响：分支导致了眼图的裕量明显下降，极有可能造成信号时序的紊乱；
最后，再介绍一篇来自于力科的文章，在这片文章中，介绍了一种利用TDR
测量技术测试电路板有效介电常数的方法，
小
编认为这个关于
TDR的拓展应用非常地有趣，感兴趣的小伙伴可以多多学习：
利用TDR快速测量介电常数Dk
小结
本文侧重于对反射原理的讨论，TDR
做为一个典型的应用，在信号完整性设计中将会大量地被运用，对于它的理解和熟练使用，也是一个不断累积的过程，在以后的工作中，如果遇到其它有趣的案例，小编会再与大家进行分享。
