滑动窗口简单概念
滑动窗口是我们
假想
出的一种数据结构,我们在这篇文章实现的窗口,能较快速的求
区间最大最小值
在一些
区间不回退
的题目中运行效率也十分优秀
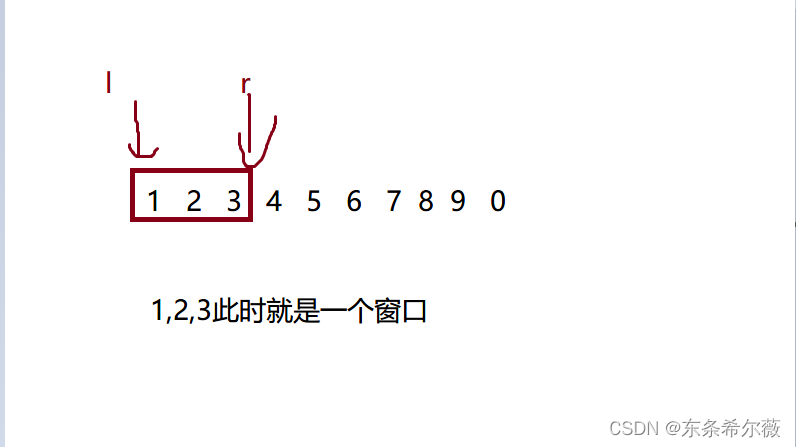
设窗口的左边界为l,右边界为r,(规定l<=r恒成立)
我们可以通过滑动右边界,从窗口的右边进入数字
也可以通过滑动左边界,从窗口左边出数字
滑动窗口求区间最大值(leetcode239)
题目描述:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
思路求解
我们可以通过
双端队列
来实现我们求最大值窗口的结构,双端队列中存储
数组中的下标
双端队列中必须始终维持根据下标对应的数字由大到小的顺序
不断的移动窗口,若进入的数会打破由大到小的平衡(即新数字大于队列末),队尾就不断出数字,直到满足双端队列的要求为止,再把当前数字插入
动图演示:

它可以表示在
固定大小窗口中,只要窗口中包含这个数字,那么这个窗口的最大值永远队头
直到窗口中没有了这个最大值,那么把它
从左边弹出
代码实现及注释:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n=nums.size();
vector<int>ans;
deque<int>qmax;//维持最大值的队列
for(int r=0;r<n;r++)
{
while(!qmax.empty()&&nums[qmax.back()]<=nums[r])
{
qmax.pop_back();//这是维持队列由大到小的结构
//将队尾所有比新数字小的数字全部弹出
}
qmax.push_back(r);
if(qmax.front()==r-k)
{
qmax.pop_front();//这是最大值对应下标已经不在窗口中的情况
//因为r-l=k
}
if(r>=k-1)
{
ans.push_back(nums[qmax.front()]);
//窗口已经成型,就直接加入数字
}
}
return ans;
}
};
求满足要求的子数组个数
题目描述:
给定一个数组arr和一个整数sum
若一个子数组(必须连接)满足子序列最大值-最小值<=sum,则称这个子数组符合要求
返回所有符合要求的子序列个数
思路求解:
我们可以先甩出两个结论:
-
如果某个子数组满足要求,那么
这个子数组的子数组都符合要求
-
如果某个子数组不满足要求,那么
以它为子数组的数组都不符合要求
为什么?
我们知道,我们最终要求的是max-min
如果满足要求了,那么max-min<sum是应该成立的
显然易见,它的子数组最大值只会比这个数组的最大值小,最小值只会比这个数组的最小值大,
所以这个情况下,max-min是只会减少的
不满足要求的同理可证
所以我们可以这样:
初始先把窗口放在最左边,
维持窗口最大和最小值
,不断更新窗口右边界,
直到不满足要求
根据结论1,从l开始的所有子数组都满足要求**(l到l+1;l到l+2;l到l+3…等子数组)**
根据结论1,我们在更新l的时候,可以不用更新r
代码和注释:
int AllLessNumSubArray(vector<int>& nums, int sum)
{
int n = nums.size();
deque<int>qmax;
deque<int>qmin;
int ans = 0;
int r = 0;
for (int l = 0; l < n; l++)
{
while (r < n)
{
while (!qmax.empty() && nums[qmax.back()] <= nums[r])
{
qmax.pop_back();
}
qmax.push_back(r);
while (!qmin.empty() && nums[qmin.back()] >= nums[r])
{
qmin.pop_back();
}
qmin.push_back(r);
//以上是维持最大最小队列
//以下是滑动窗口
if (nums[qmax.front()] - nums[qmin.front()] <= sum)
{
r++;
}
else
{
break;
}
}
ans += r - l;
//更新过期元素
if (qmax.front() == l)
{
qmax.pop_front();
}
if (qmin.front() == l)
{
qmin.pop_front();
}
}
return ans;
}
以上都是题目中明确要求求窗口最大最小值的,下面这道题就不太明显了
加油站最佳出发点
题目描述
给你两个数组,gas和cost
其实gas[i]表示第i号加油站的油量,cost[i]表示从i号到i+1号加油站消耗的油量
车初始油量为0
返回一个bool类型,表示第i号加油站出发,车能不能完整绕过一圈,
只能逆时针绕圈
例如:
gas=[1,1,3,1]
cost=[2,2,1,1]
图如下:
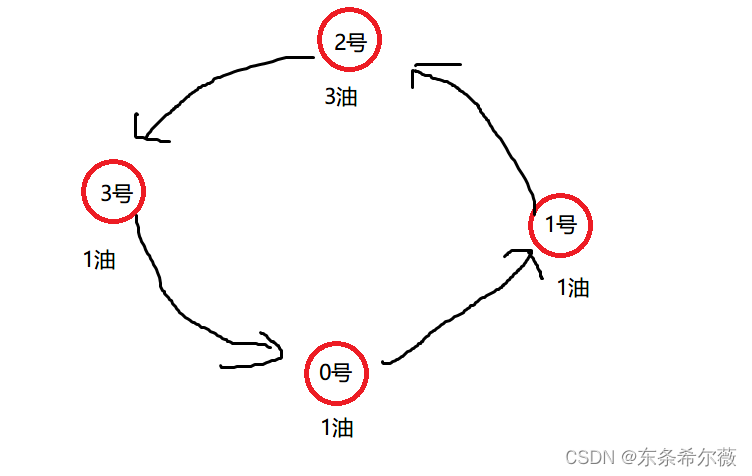
如果你从0号加油站出发,cost[0]是2,但gas[0]=1,车不能到1号加油站,所以ans[0]返回false
总体返回:[0,0,1,0]
思路求解:
我们在解题前,可以先进行一个加工
先将gas和cost每个位置对应数字相减,得到处理后的数组nums
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
}
这样就能表示出
从某一站出发,能不能到达它的下一站,如果结果为负数,则不能到达
我们可以求出
前缀和
,如果中途出现了负数,表示这一圈不能够完成
例如:从0开始的前缀和,表示从0出发,中途途径每个加油站的剩余油量
从1开始的前缀和,表示从1出发,以此类推
因为我们要绕一圈,所以我们应该处理出两倍的原数组大小(不从0开始出发?)
int m=n<<1;
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
nums[i + n] = gas[i] - cost[i];
}
for (int i = 1; i < m; i++)
{
nums[i] += nums[i - 1];
}
我们本题的窗口要求大小与原数组相同,我们可以这样处理我们的数组:
维持最小值窗口
显而易见,如果最小值不是负数,那么窗口中就没有负数了
在更新数组窗口时,我们记得把窗口中的值
减去窗口左边界前面一个值,这样就才是正确的从l开始的前缀和
直接判断当前最小值是否小于0即可
代码即注释:
vector<bool> GasStation(vector<int>& gas, vector<int>& cost)
{
int n = gas.size();
int m = n << 1;
vector<bool>ans(n, false);
int* nums = new int[m];
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
nums[i + n] = gas[i] - cost[i];
}
for (int i = 1; i < m; i++)
{
nums[i] += nums[i - 1];
}
deque<int>w;
//初始化窗口
for (int i = 0; i < n; i++)
{
while (!w.empty() && nums[w.back()] >= nums[i])
{
w.pop_back();
}
w.push_back(i);
}
for (int offset = 0, i = 0, j = n; j < m; offset = nums[i++], j++)
{
//offset表示窗口前面的数字,w始终维持窗口最小值
//i左边界,j右边界
if (nums[w.front()] - offset >= 0)
{
ans[i] = true;
}
if (w.front() == i)
{
w.pop_front();
}
while (!w.empty() && nums[w.back()] >= nums[j])
{
w.pop_back();
}
w.push_back(j);
}
delete[]nums;
return ans;
}