博客

最小生成树

  • Post author:
  • Post category:其他




课程小结



定义



(1) 定义



生成树：

树：N个点，N – 1条边的连通图

生成树：包含某图G所有点的树

一个图G是树当且仅当以下任意一个条件成立

G有V-1条边，无环

G有V-1条边，连通

任意两点只有唯一的简单路径

G连通，但删除任意一条边后不连通



最小生成树：

一个有N个结点的连通图是原图的极小连通子图，且包含原图中的所有N个节点，并且有保持图连通的最少的边。

在一给定的无向图G = (V, E)中，(U, V) 代表连接U和V的边， 而w(U, V)代表此边的权重，若存在T为E的子集且为无环图，使得联通所有节点的w(T)最小，则此T为G的最小生成树。


生成树

：一个|V|个点的的图，取其中|V| – 1条边，并连接所有的顶点，则组成原图的一个


生成树


。

属性：|V| – 1条边、连通、无环。


最小生成树

：加权图的最小生成树是一棵


生成树


，其所有边的权值之和不会大于其它任何生成树。

简单讲：


找到连接所有点的最低成本路线


。

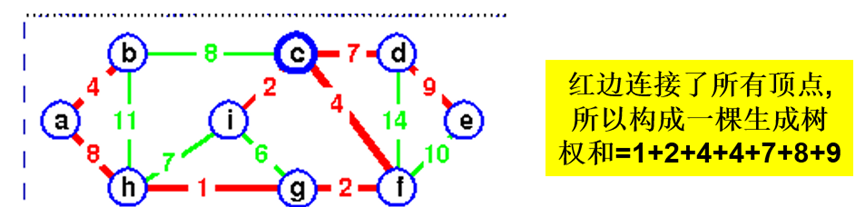
最小生成树图片

最小生成树可以用Prim (普里姆) 算法或 Kruskal (克鲁斯卡尔) 算法求出。



原理

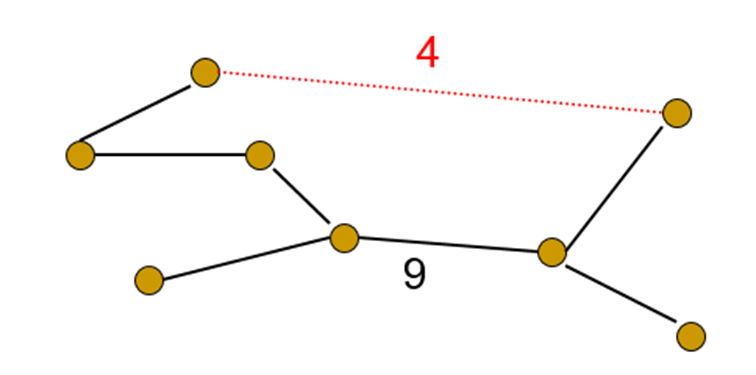
  1. 环属性：一棵生成树上，增加一条边E，再删除E所在环上的最大边，会得到一个“更好”的生成树 (如果E不是最大边)

    最小生成树图片
  2. 剪切属性：在图中，剪切将顶点划分成两个不相交集合。交叉边为地些顶点在两个不同集合的边。对于任何一个剪切，各条最小的交叉边都属于某个MST，且每个MST中都包含一条最小交叉边。

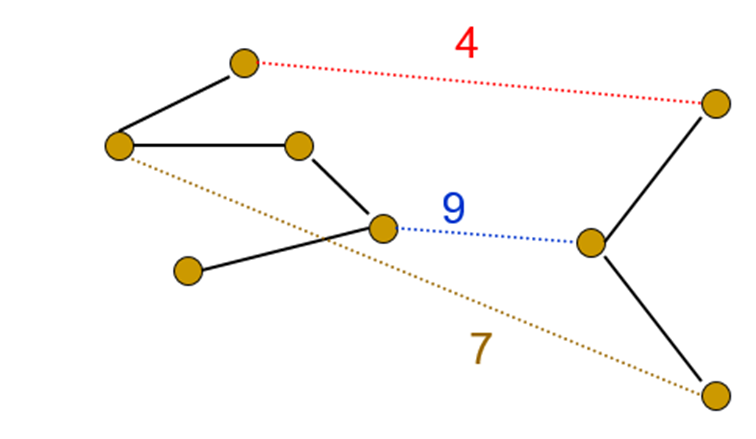
    最小生成树图片
  3. 最小边原则：图中权值最小的边(如果唯一的话)一定在最小生成树上。
  4. 唯一性：一棵生成树上，如果各边的权都不相同，则最小生成树是唯一的。反之不然。



Prim算法

  1. 输入：一个加权连通图，一个加权连通图，其中顶点集合为V，边集合为E；

  2. 初始化：Include = {StartId}。

  3. 重复下列操作，直至Include = V:

    1. 在集合E中选取权值最小的边<V1, V2>，其中V1为集合Include中的元素，而V2不在Include集合当中；
    2. 把V2加入Include中。

  4. 输出：使用集合Include来描述得到的最小生成树。 

MST_Prim(G, r)   //从任意点r出发，生长成一MST
	for i=1 to n do
		dis[i] <- ∞ // 初始化每点到Vnew集合的最小值
		Vnew[i] <- false //设顶点不在Vnew中

	dis[r] <- 0 //将r设为0（或- ∞ ），准备取出
	for i=1 to n do
		v <- get-min() //取dis[?]中最小的值c和顶点v,
		Vnew[ v ] <- true //v放入Vnew中
		sum <- sum+c //c加入MST的总和中
		updata( v ) //枚举交叉边(v,B),改进dis[ ]


#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define Inf 0x7f7f7f7f
#define MemInf 0x7f
int Node, Edge, Node1, Node2, Weight;
int Graph[105][105];
bool Include[105];
int Dis[105];
struct Get_Min_Return_Value_Node {
	int Node;
	int Weight;
};
void Update(int NodeId) {
	for (int i = 1; i <= Node; i++) {
		if (Include[i] == false && Graph[NodeId][i] != Inf) {
			Dis[i] = min(Dis[i], Graph[NodeId][i]);
		}
	}
}
Get_Min_Return_Value_Node Get_Min( ) {
	Get_Min_Return_Value_Node Result = { 0,0x7f7f7f7f };
	for (int i = 1; i <= Node; i++) {
		if (Include[i] == false && Dis[i] < Result.Weight) {
			Result.Node = i;
			Result.Weight = Dis[i];
		}
	}
	return Result;
}
int Make_MST(int StartId) {
	memset(Dis, MemInf, sizeof(Dis));
	memset(Include, false, sizeof(Include));
	Dis[StartId] = 0;
	int Result = 0;
	for (int i = 1; i <= Node; i++) {
		Get_Min_Return_Value_Node Current_Result = Get_Min( );
		Include[Current_Result.Node] = true;
		Result = Result + Current_Result.Weight;
		Update(Current_Result.Node);
	}
	return Result;
}
int Prim( ) {
	int Result = Inf;
	for (int i = 1; i <= Node; i++) {
		Result = min(Result, Make_MST(i));
	}
	return Result;
}
int main( ) {
	cin >> Node >> Edge;
	memset(Graph, MemInf, sizeof(Graph));
	int Sum = 0;
	for (int i = 1; i <= Edge; i++) {
		cin >> Node1 >> Node2 >> Weight;
		Graph[Node1][Node2] = Graph[Node2][Node1] = Weight;
		Sum = Sum + Weight;
	}
	cout << Sum - Prim( ) << '\n';
	return 0;
}



Kruskal算法

  1. 先构造一个只有N个顶点，而边集为空的子图，若将子图的各个顶点看成是各棵树上的根节点，则它是一个含有N棵树的一个森林。
  2. 从边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；
  3. 反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。


算法描述

:

MST_Kruskal(G)

(1)将G所有条边按权从小到大排序；图MST开始为空

(2)从小到大次序取边(V1,V2)

(3)若加入边(V1,V2)，MST就有环，则放弃此边，转(2)

(4)将边(V1,V2)加入MST，如果已经加了N – 1条边，结束。否则，转 (2)



伪代码

MST_Kruskal(G)
	for i=1 to n do f[i] <- i; //初始化并查集
sort( e, e+m); //边按大小排序
c <- 0; //取边的计数器
for i=1 to m do //从小到大取边
v <- find_set( e[i].v ); //左端点所在连通块“根”
u <- find_set( e[i].u ); //右端点所在连通块“根”
if(v != u) //如果不在同一连通块
	union(v,u); //合并两连通块
	sum += g[v][u]; //加入这条边的权
	if (++c == n-1) break; //if 取了n-1条边，结束



代码

//头文件
#include <iostream>
#include <algorithm>

//简化代码
using namespace std;

//常量
const int Inf = 0x3f3f3f3f;

//变量、数组
struct Edge_Node {
	int Node1, Node2, Weight;
};
int Node, Edge;
Edge_Node Edges[200005];

//排序函数
bool Compare_Function(Edge_Node Edge_A, Edge_Node Edge_B) {
	return Edge_A.Weight < Edge_B.Weight;
}

//并查集
int UFS[20005];
void Init( ) {
	for (int i = 1; i <= Node; i++) UFS[i] = i;
}
int Find(int Id) {
	int Result = Id;
	for (; UFS[Result] != Result; Result = UFS[Result]);
	for (int i = Id; UFS[i] != i;) {
		int Next = UFS[i];
		UFS[i] = Result;
		i = Next;
	}
	return Result;
}
void Union(int Root_A, int Root_B) {
	UFS[Root_B] = Root_A;
}

//算法
int Node_Num;
int Kruskal( ) {
	Init( );
	sort(Edges + 1, Edges + Edge + 1, Compare_Function);
	Node_Num = 0;
	int Sum = 0;
	for (int i = 1; i <= Edge; i++) {
		int Root_1 = Find(Edges[i].Node1), Root_2 = Find(Edges[i].Node2);
		if (Root_1 != Root_2) {
			Union(Root_1, Root_2);
			Sum += Edges[i].Weight;
			Node_Num++;
			if (Node_Num == Node - 1) break;
		}
	}
	return Sum;
}

//主函数
int main( ) {
	cin >> Node >> Edge;
	int Sum = 0;
	for (int i = 1; i <= Edge; i++) {
		cin >> Edges[i].Node1 >> Edges[i].Node2 >> Edges[i].Weight;
		Sum += Edges[i].Weight;
	}
	int Ans = Kruskal( );
	if (Node_Num != Node - 1) cout << -1;
	else cout << Sum - Ans << '\n';
	return 0;
}