博客

这些题目都是斐波那契类型得动态规划题目，他们得递推公式都是dp[i]=dp[i-1]+dp[i-2]这种形式，但是确定地推公式得时候我们都需要明确的知道递推公式下标为i处dp[i]代表什么意思。

1.

力扣509.斐波那契数

本题题目中已经给出了递推公式，所以我们只需要定义好数组就可以，最终返回dp[n]。

   public int fib(int n) {
        //过滤特殊情况
        if(n==0){
            return 0;
        }
        //定义dp数组
        int[] dp = new int[n+1];
        dp[0] = 0;
        dp[1] = 1;
        //循环计算出数组得值
        for(int i=2;i<=n;i++){
            dp[i] = dp[i-1] +dp[i-2];
        }
        return dp[n];
    }

2.

力扣70.爬楼梯

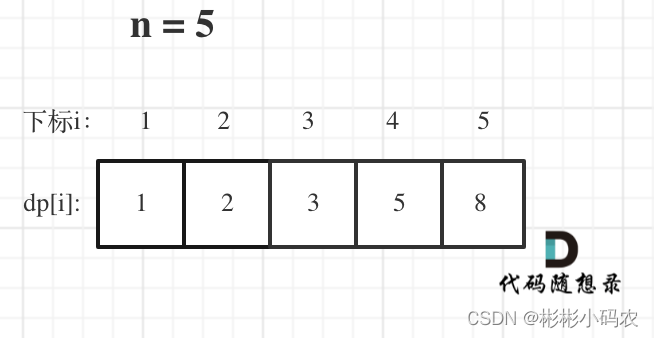
我们定义数组得含义是，下标为i时dp[i]为到达这个台阶有多少种得可能，加入我们在台阶为3处，我们只能从1台阶或者2台阶处分别走2步和1步到达3台阶处，且台阶3处得可能性就为1和2处得可能性相加。递推公式：dp[i]=dp[i-1]+dp[i-2];

    public int climbStairs(int n) {
        //过滤特殊情况
        if(n<=2){
            return n;
        }
        //确定递推数组
        int[] dp = new int[n+1];
        dp[1] = 1;
        dp[2] = 2;
        //循环确定数值
        for(int i=3;i<=n;i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

3.

力扣746.使用最小花费爬楼梯

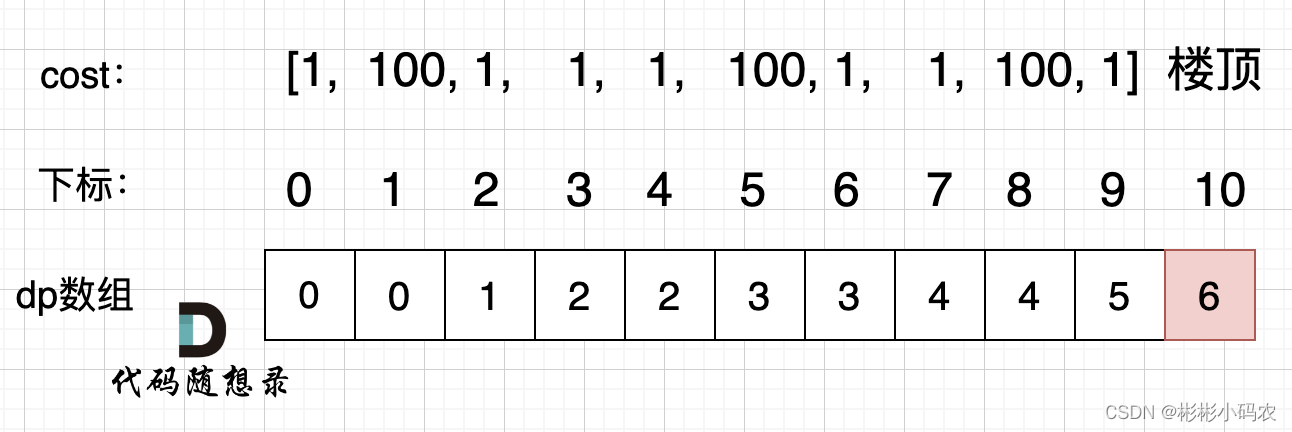
感觉的这题最主要就是理解题目得意思，首先我们可以选择起跳得位置0或1，从这个位置起跳是需要花费cost[i]得费用，到我们循环跳出数组即为到达房顶，而本题要我们求出最小得花费，所以我们需要求出从i-1和i-2跳到i处得最小值，又因为是总花费，所以还需要加上本来在i-1或i-2处得花费。

    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length+1];
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<=cost.length;i++){
            //本题得关键，比较两个起跳位置求出花费最小
            dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.length];
    }