前言:
链表是数据结构里面最开始的章节,也是对新手的理解有困难的第一章。笔者大二下学校才开设数据结构,以防自己忘记,遂记录之。
链表的概念:
链表是一种物理
存储单元
上非连续、非顺序的
存储结构
,
数据元素
的逻辑顺序是通过链表中的
指针
链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储
数据元素
的数据域,另一个是存储下一个结点地址的
指针
域。
由以上定义我们可知道单链表的组成。单链表由
头指针
,
头结点
,
结点
组成。头指针是找到一个链表的关键,头结点可以帮助我们更好的操作链表,头结点的指针域指向第一个结点,头结点的数据域可以用来记录表长,但是我习惯于赋0。一个结点分为
指针域
跟
数据域
。通过指针域可以找到下一个结点。最后一个结点的指针域为NULL,这可以作为遍历结束的标志。
链表的优势:
相对于线性表:
①链表对于长度定义不死板,可以随时插入元素,增加表长。
②线性表在插入和删除元素时,要移动大量的元素,而链表插入和删除操作简单。
链表的相关操作:
定义:
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
// 定义相关返回值
const int OK = 1;
const int ERROR = 0;
// 元素类型与返回状态的别称
typedef int ElemType;
typedef int Status;
// 节点,链表定义
typedef struct Lnode {
ElemType data; //数据域
struct Lnode *next; //指针域
}Lnode,*LinkList; // 这里的*LinkList 等价于 Lnode * Lnode是一个结点,LinkList相当于头指针
初始化的操作
这里的初始化便创建了一个带有头结点的链表,之后可以用LinkList L找到这个链表,所以L最好是不要移动或者是改变指向。
//链表的初始化
Status InitList(LinkList & L) { //这里是地址传递,如果要改变L的值就传地址,否则会copy一份操作,这样就不会改变L
L = new Lnode; //创建头节点
L->next = NULL;
L->data = 0;
return OK;
}
链表的创建,前插法与尾插法
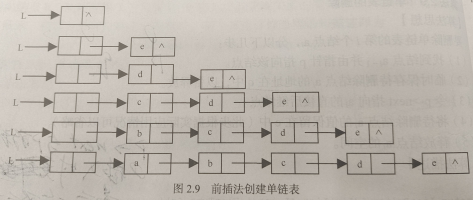
前插法:
思路:有个头指针永远指向最左边的元素,新建的元素的指针域先接头结点的的指针域(即NULL),然后再将头结点指向该结点。关键的步骤在于s->next = L->next;L->next = s;
值得注意的是:这种创建方法的元素存储顺序是与逻辑顺序相反的!
void CreateList_F(LinkList &L, int n) {
//创建的一开始都要先初始化
L = new Lnode;
L->next = NULL;
L->data = 0;
for (int i = n; i > 0; i--) {//这里的n的作用就是用来计数的
LinkList s = new Lnode;
cin >> s->data;
s->next = L->next;
L->next = s;
}
}
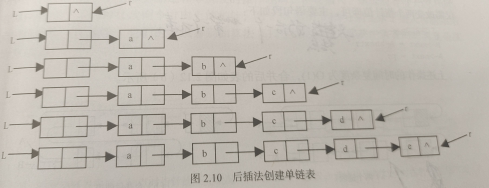
尾插法:
思路:初始化该链表的同时用一个尾指针永远指向链表的最后一位,每新建一个结点,新节点的指针域都赋值为NULL,然后连接到r的指针域上去,r指针移动到新节点上,这样r又是指向最后的结点了。关键操作:s->next = NULL;r->next = s; r= s;
//链表的创建 --- 尾插法(与逻辑顺序相同)
void CreateList_R(LinkList& L, int n) {
L = new Lnode;
L->next = NULL;
//尾插法要用尾指针
LinkList R = L;
for (int i = 0; i < n; i++) {
LinkList s;
s = new Lnode; //这里别忘记了s应指向一个新的结点
cin >> s->data;
s->next = NULL;
R->next = s;
R = s;
}
}
链表的打印
这里提供两种方法:第一种是while遍历,第二种是递归的思想。
这里如果是直接传入L而不是&L,也不需要p来充当遍历指针,直接移动头结点就可以了。
在用第二种方法的时候,是要从头结点开始遍历的,所以最好给头结点的data赋值,要不然就是随机分配的数字了。
//使用while
void PrintList(LinkList& L) {
if (L == NULL) {
cout << "链表已空" << endl;
return;
}
LinkList p = L->next;
while (p) {
cout << p->data << " ";
p = p->next;
}
cout << endl;
}//递归
void PrintList(LinkList L){
if(!L) return;
cout<<L->data<<" ";
PrintList(L->next);
}
链表的插入操作
想插入到ai的位置,必须先找到ai-1的位置。并且插入是可以插入到第一个跟最后一个元素的位置上的。所以这里j从0开始,结束条件是j<i-1。出了循环如果找到了就是i-1的位置。这里p=L,是从头结点开始遍历的,这样可以插到第一个元素。while里面写p,保证插到最后一个元素上。
//链表的插入操作
Status AddList(LinkList& L, int i, ElemType e) {
LinkList p = L;
int j = 0;
//这里是p而不是p->next,这样写可以在最后一位插入数,p->next的话最后一位不能插入,删除是这样写的
//j<i-1的意思是找到ai-1
while (p && j < i - 1) {
p = p->next;
j++;
}
if (!p || j > i - 1) return ERROR; // 没找到直接return
LinkList s = new Lnode; //这里的Linklist 跟Londe *含义一样,但是我们一般使用Linklist,符合定义习惯
s->data = e; // s的含义是s指向的节点,s->的含义是指向s的下一个节点
s->next = p->next;
p->next = s;
return OK;
}
链表的删除操作
想删除第ai个元素,必须找到第ai-1个元素的位置。值得注意的是①这里的while中的条件应该是p->next。(最后一个结点是不会作为ai-1的)②删除一个元素要释放空间(delete)
//删除第ai个元素 ,并用e带回返回值
Status DeleteListElem(LinkList &L,int i,ElemType &e){
int j = 0;
LinkList p = L;
while(p->next&&j<i-1){
p = p->next;
j++;
}
if(!(p->next)||j>i-1) return ERROR;
Linklist q;
q = p ->next;
e = q ->data;
p->next = q->next;
delete q;
return OK;
}
链表的查询操作
这里提供按序号查询的操作
思想就是遍历,找到了就返回。
//链表的按序号查找 直接找到ai就行了
Status GetElem(LinkList L, int i, ElemType& e) { //找到的元素赋值给e
LinkList p = L->next; //不要考虑开头与结尾 直接从第一个元素开始即可
int j = 1; // 这里的j从1开始,因为不要考虑ai-1!但是插入删除要考虑ai的前一个元素,所以从0开始!!
while (p && j < i) { //j<i如果有结果,那就是j=i
p = p->next;
j++;
}
if (!p || j > i) return ERROR; //没有找到return掉
e = p->data;
return OK;
}
链表的排序操作
这里可以用冒泡,选择排序等,但是笔者在其他地方看到的一个简单的操作但是可以提高排序的速度。
思路就是先放到顺序表中,然后用sort排序,再放回链表中。这样最快有nlogn的速度。
// 求链表长度
int LengthList(LinkList& L) {
int n = 0;
LinkList q = L->next; // 从头节点开始
while (q) {
q = q->next;
n++;
}
return n;
}
//前提是知道链表的长度
//链表的排序 先全放到数组中,然后对数组排序,最后再放回链表中,这样做比冒泡要快nlogn <n^2
void SortList(LinkList& L) {
int length = LengthList(L);
ElemType *arr = new ElemType[length]; // c++开辟空间的语法 指针 = new 类型[个数];
//if (Is_Empty(L)) return;
int i = 0;
LinkList p = L->next;
//遍历链表,全放数组里
while (p) {
arr[i] = p->data;
i++;
p = p->next;
}
// 这里一定要重新改变i跟p的指向
i = 0;
p = L->next;
//对数组排序
sort(arr, arr + length);
//再全放入链表中
while (p) {
p->data = arr[i];
i++;
p = p->next;
}
}
有序链表的合并
生成升序链表
// 两个链式表的合并
// 前提是两个链表是有序的
void mergeList_L(LinkList& La,LinkList &Lb,LinkList &Lc) {
//开始的时候用pa,pb分别指向LaLb的第一个元素,Lc指向La的头节点
LinkList pa = La ->next;
LinkList pb = Lb->next;
Lc = La;
LinkList pc = Lc;
//当la或者lb一者为空时,结束比较
//循环条件为pa&&pb
while (pa && pb) {
if (pa->data <= pb->data) { //La的元素小
pc->next = pa; pc = pa; pa = pa->next;
}
else {
pc->next = pb; pc = pb; pb = pb->next;
}
}
pc->next = pa ? pa : pb;
//用La做表头,所以释放Lb的空间
delete Lb;
}
生成降序
void mergeList(LinkList l1, LinkList l2, LinkList &l3) { // 要用到头插法 因为头插法的插入顺序是与逻辑顺序相反的
LinkList p1 = l1->next;
LinkList p2 = l2->next;
l3 = l1;
l3->next = NULL; // 使用头插法
LinkList s; // 工作指针指向插入节点
while (p1 && p2) {
if (p1->data < p2->data) { // p2比较大的话
s = p1;
p1 = p1->next;
s->next = l3->next;
l3->next = s;
}
else {
s = p2;
p2 = p2->next;
s->next = l3->next;
l3->next = s;
}
}
if (!p1) p1 = p2;
while (p1) { //全部头插法到l3
s = p1;
p1 = p1->next;
s->next = l3->next;
l3->next = s;
}
}
链表的反转
三指针法
int inverse(LinkList& L) { //三指针法
if (L->next->next == NULL) return -1;
LinkList r = L;
LinkList p = L->next;
LinkList q = L->next->next;
while (q) {
p->next = r;
r = p;
p = q;
q = q->next;
}
p->next = r;
L->next->next = NULL;
L->next = p;
return 1;
}
链表的题目还是要多画图,这样好理解。
算法初学者且第一次发帖,如果有错请告知!