
梁政:机器人工程师进阶之路(七)旋量法(下)zhuanlan.zhihu.com

从上两篇我们可以了解到,利用旋量法可以在螺旋运动中获得螺旋轴(screw axis)
。通过螺旋轴可以将坐标系变换矩阵T矩阵
转化为指数形式
其中
。
另外,和T矩阵的左乘右乘一样,要区分当前坐标系是相对于固定坐标系{S}变换还是自身坐标系{B}变换。而且两者之间的螺旋轴的变换关系为
根据这些,我试着给Innfos-Gluon建个模。之前的DH法,按着自己的想法去建立模型,到后面的计算变得很复杂。所以还是太年轻,这次我就不给自己添加难度了,模仿大佬们的模型建立吧。
Gluon模型
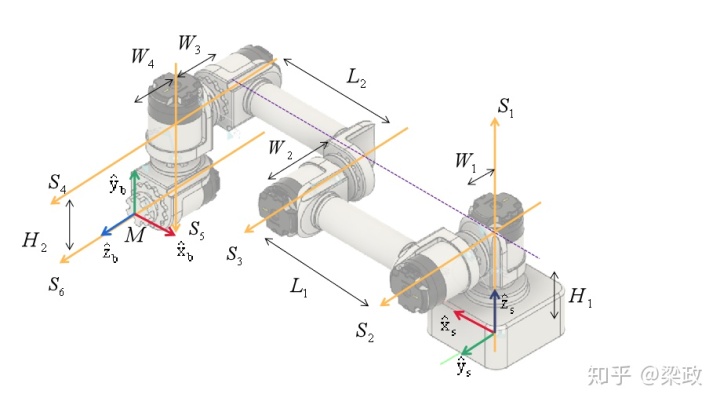
我们设定基坐标系为固定坐标系{s},末端坐标系{b}。确定好各关节轴线,以及坐标系原点为轴线相交点,类似于DH法。并在{s}下,确定末端位姿T矩阵为M。
指数积公式(Product of Exponentials(PoE) Formula)
我们分两个方向进行建模。
1. 螺旋轴在基坐标系中,也就是固定坐标系{s};
2. 螺旋轴在末端坐标系中,也就是自身坐标系{b};
在T矩阵时,固定坐标系就是左乘,自身坐标系就是右乘。把指数积等价于T矩阵,所以也一样。
-
在基坐标系上的螺旋轴
-
确定螺旋轴。我们的机械臂都是旋转副,那么各自必然有一个旋转轴
。同时相对于坐标原点会产生一个线速度方向
。合起来将得到螺旋轴
。例如,第4关节如下图。
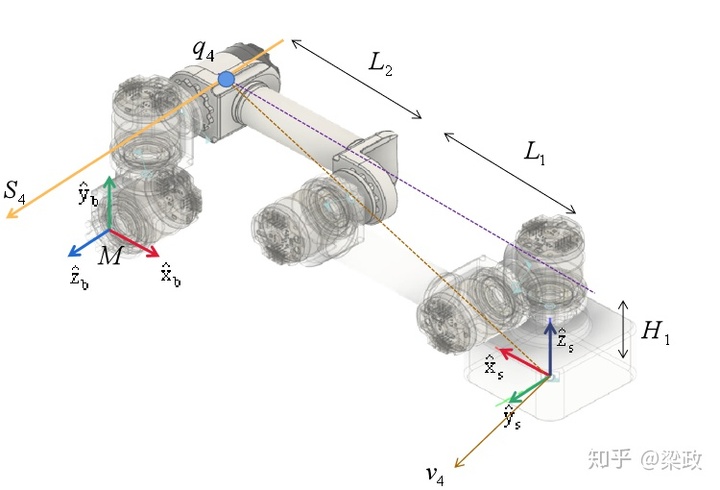
我们可设第4关节得旋量为
,
,
那么螺旋轴可被计算为
2. 将所有螺旋轴记录下,并列表。
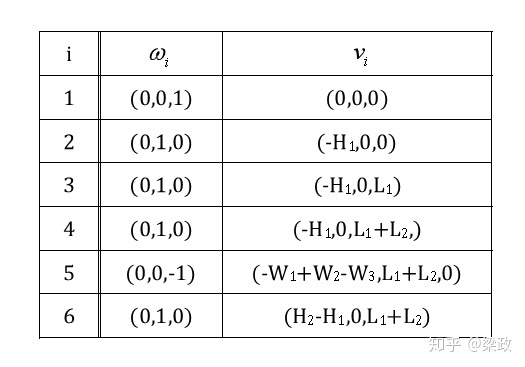
3. 左乘各T矩阵的指数形式,得到PoE公式。
-
在末端坐标系下的螺旋轴
-
同样,先找到螺旋轴
,只不过这次是相对于末端坐标系的。同样是第4关节,
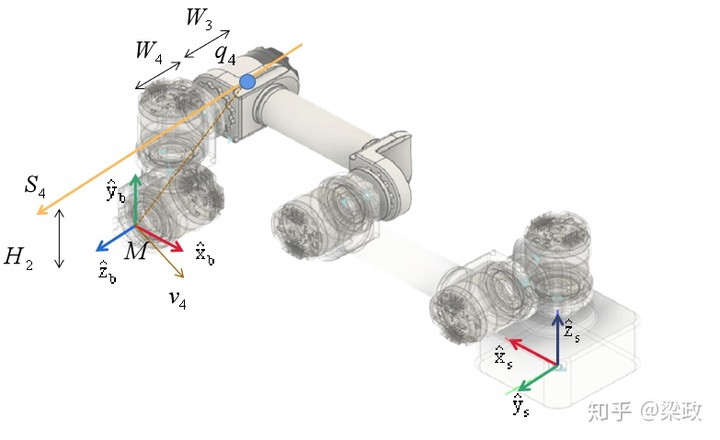
,
,螺旋轴可被计算为
2. 将所有螺旋轴记录下,并列表。
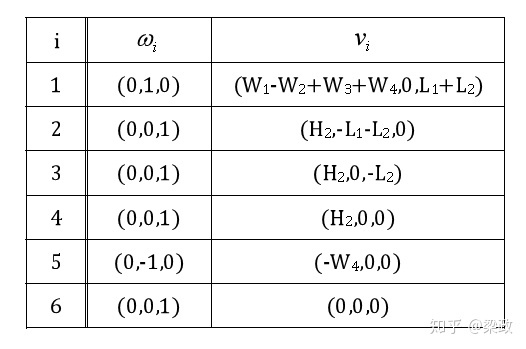
3. 左乘各T矩阵的指数形式,得到PoE公式。
4. 若相对于末端坐标系,那么我们可以通过螺旋轴变换关系来求PoE公式。已知末端相对于固定坐标系的变换矩阵为
,那么
根据矩阵指数性质,
,变换矩阵可改写为
Matlab正运算仿真
H1=105.03;W1=80.09;L1=174.42;W2=84.51;L2=174.42;W3=80.09;H2=80.09;W4=44.36;
M=[-1 0 0 L1+L2;0 0 1 W1-W2+W3+W4;0 1 0 H1-H2;0 0 0 1] % Home Configuration of End-Effector
%% Spatial Twist
Slist = [[0; 0; 1; 0; 0; 0], ...
[0; 1; 0; -H1; 0; 0],...
[0; 1; 0; -H1; 0; L1],...
[0; 1; 0; -H1; 0; L1+L2],...
[0; 0; -1; -W1+W2-W3; L1+L2;0],...
[0; 1; 0; H2-H1; 0; L1+L2]]; %The joint screw axes in the space frame
thetalist = [pi/6; pi/6; pi/6; pi/6; pi/6; pi/6];
Ts=FKinSpace(M,Slist,thetalist)
%% Body Twist
Blist = [[0; 1; 0; W1-W2+W3+W4; 0; L1+L2], ...
[0; 0; 1; H2; -L1-L2; 0],...
[0; 0; 1; H2; -L2; 0],...
[0 ;0; 1; H2; 0; 0],...
[0; -1; 0; -W4; 0;0],...
[0; 0; 1; 0; 0; 0]]; %The joint screw axes in the end-effector frame
thetalist = [pi/6; pi/6; pi/6; pi/6; pi/6; pi/6];
Tb=FKinBody(M,Blist,thetalist)
%%
function T = FKinSpace(M, Slist, thetalist)
T = M;
for i = size(thetalist): -1: 1
T = MatrixExp6(VecTose3(Slist(:, i) * thetalist(i))) * T;
end
end
%%
function T = FKinBody(M, Blist, thetalist)
T = M;
for i = 1: size(thetalist)
T = T * MatrixExp6(VecTose3(Blist(:, i) * thetalist(i)));
end
end
%%
function T = MatrixExp6(se3mat)
omgtheta = so3ToVec(se3mat(1: 3, 1: 3));
if NearZero(norm(omgtheta))
T = [eye(3), se3mat(1: 3, 4); 0, 0, 0, 1];
else
[omghat, theta] = AxisAng3(omgtheta);
omgmat = se3mat(1: 3, 1: 3) / theta;
T = [MatrixExp3(se3mat(1: 3, 1: 3)), ...
(eye(3) * theta + (1 - cos(theta)) * omgmat ...
+ (theta - sin(theta)) * omgmat * omgmat) ...
* se3mat(1: 3, 4) / theta;
0, 0, 0, 1];
end
end
%%
function se3mat = VecTose3(V)
se3mat = [VecToso3(V(1: 3)), V(4: 6); 0, 0, 0, 0];
end
%%
function so3mat = VecToso3(omg)
so3mat = [0, -omg(3), omg(2); omg(3), 0, -omg(1); -omg(2), omg(1), 0];
end
%%
function omg = so3ToVec(so3mat)
omg = [so3mat(3, 2); so3mat(1, 3); so3mat(2, 1)];
end
%%
function judge = NearZero(near)
judge = norm(near) < 1e-6;
end
%%
function [omghat, theta] = AxisAng3(expc3)
theta = norm(expc3);
omghat = expc3 / theta;
end
%%
function R = MatrixExp3(so3mat)
omgtheta = so3ToVec(so3mat);
if NearZero(norm(omgtheta))
R = eye(3);
else
[omghat, theta] = AxisAng3(omgtheta);
omgmat = so3mat / theta;
R = eye(3) + sin(theta) * omgmat + (1 - cos(theta)) * omgmat * omgmat;
end
end从结果看出,两种建模方式是一样的。若将角度设为
,结果为

与之前DH法中直立的初始位置是相同的,由于末端坐标轴的x,z轴相反,所以姿态矩阵不一样。
梁政:机器人工程师进阶之路(三)6轴机械臂DH法下的变换关系zhuanlan.zhihu.com