目录
1. 渐进记号Θ、Ο、o、Ω、ω的定义及其使用
1)渐近
紧确界
记号:Ɵ(big-theta):

由下图中左侧f(n)=Θ(g(n))图可以看出,对所有n>n0时,函数f(n)乘一个常量因子可等于g(n),我们称g(n)是f(n)的一个
渐近紧确界
。Θ记号在五个记号中,要求是最严格的,因为g(n)即可以表示上界也可以表示下界。

需要注意的是:Θ(g(n))的定义要求每个成员f(n)∈Θ(g(n))均
渐近非负
,即当n足够大时,f(n)非负。
渐近正函数
就是对所有足够大的n均为正的函数。
2)渐近上界记号:O(big-oh)
定义:设f(n)和g(n)是定义域为自然数集N上的函数。
若存在
正数
c
和
n0
,使得对一切
n
≥
n0
都有
0
≤
f(n)
≤
cg(n)
成立,则称
f(n)
的渐进的上界是
g(n)
,记作
f(n)=O(g(n))
。通俗的说n满足一定条件范围内,函数f(n)的阶不高于函数g(n)。
根据符号O的定义,用它评估算法的复杂度得到的只是问题规模充分大时的一个上界。这个上界的阶越低,评估越精确,越有价值。

几种常见的复杂度关系
O(1)<O(log(n))<O(n)<O(nlogn)<
<
<O(n!)<
需要注意的是:对数函数在没有底数时,默认底数为2;如lgn=logn=log2n 因为计算机中很多程序是用二分法实现的。
符号用法测试:素数测试
int isprime(int n) {
for(int i=2; i<=(int)sqrt(n); i++) {
if(n%i==0) {
return0;
}
}
return1;
}
在上面这个素数测试的例子中,基本运算是整除;时间复杂度T(n)=
是正确的。当被测的数n为偶数时,基本运算一次也没执行,所以T(n)=
是错误的,因为没有办法证明T(n)的下界是
3)渐近下界记号:Ω(big-omega)
定义:设f(n)和g(n)是定义域为自然数集N上的函数。若存在正数c和n0,使得对一切n≥n0都有0≤cg(n)≤f(n)成立,则称f(n)的渐进的下界是g(n),记作f(n)=Ω(g(n))。通俗的说n满足一定条件范围内,函数f(n) 的阶不低于函数g(n)。
根据符号Ω的定义,用它评估算法的复杂度得到的只是问题规模充分大时的一个下界。这个下界的阶越高,评估越精确,越有价值。
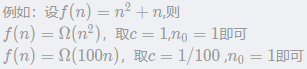
显然,Ω(n2) 作为下界更为精确。
4)非渐近紧确上界:o(小-oh)
定义1:设f(n)和g(n)是定义域为自然数集N上的函数。若对于任意正数c,都存在n0,使得对一切n≥n0都有0≤f(n)由O记号提供的渐近上界可能是渐近紧确的,也可能是非紧确的。(如:2
=O(
)是渐近紧确的,而2n=O(
)是非紧确上界。)
例子:f(n)=
+n则f(n)=o(
)
5)非渐近紧确下界:ω(小-omege)
定义1:设f(n)和g(n)是定义域为自然数集N上的函数。若对于任意正数c,都存在n0,使得对一切n≥n0都有0≤cg(n)
ω记号与Ω的关系类似于o和O记号的关系。我们用ω表示一个非渐近紧确的下界。
例子:f(n)=
+n,则f(n)=ω(n)是正确的。f(n)=ω(
)则是错误的,f(n)=Ω(
)是正确的。
2. 渐近记号Θ、Ο、o、Ω、ω关系
给出这些记号的定义:

对于定义的注意点:
(1)这些定义的前提是f(n)和g(n)是渐近非负的,渐近非负的意思是“当n趋于无穷大时,f(n)和g(n)都非负”。
(2)对于第4和第5条定义,需要注意是对于任意的c。
用集合论来表示这5个符号的关系:
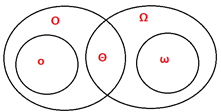
从上面的图可以看出:
(1)如果f(n)=Θ(g(n)),则f(n)=O(g(n))且f(n)=Ω(g(n))。
(2)如果f(n)= o (g(n)),则f(n)=O(g(n))。
(3)如果f(n)=ω(g(n)),则f(n)=Ω(g(n))。
(4)如果f(n)=O(g(n)),则要么是f(n)= o (g(n)),要么是f(n)=Θ(g(n))。
(5)如果 f(n)=Ω(g(n)) ,则要么是f(n)=ω(g(n)),要么是f(n)=Θ(g(n))。
记号 含义 通俗理解
(1)Θ(西塔)紧确界。相当于”=”
(2)O (大欧)上界。相当于”<=”
(3)o(小欧)非紧的上界。相当于”<”
(4)Ω(大欧米伽)下界。相当于”>=”
(5)ω(小欧米伽)非紧的下界。相当于”>”
3. 和式界的证明方法