函数依赖
一. 概念
1. 函数依赖定义
设
R
(
U
)
R(U)
R
(
U
)
是属性集合
U
=
A
1
,
A
2
,
.
.
.
,
A
n
U = {A_1, A_2,…,A_n}
U
=
A
1
,
A
2
,
.
.
.
,
A
n
上的一个关系模式,
X
,
Y
X, Y
X
,
Y
是
U
U
U
上的两个子集,若对
R
(
U
)
R(U)
R
(
U
)
的任意一个可能的关系
r
r
r
,
r
r
r
中不可能有两个元组满足在
X
X
X
中的属性值相等而在
Y
Y
Y
中的属性值不等,则称 “
X
X
X
函数决定
Y
Y
Y
” 或“
Y
Y
Y
函数依赖于
X
X
X
”,记作
X
→
Y
X \rightarrow Y
X
→
Y
例子1:
U
=
{
学
号
,
姓
名
,
年
龄
,
班
号
,
班
长
,
课
号
,
成
绩
}
U = \{学号, 姓名, 年龄, 班号, 班长, 课号, 成绩\}
U
=
{
学
号
,
姓
名
,
年
龄
,
班
号
,
班
长
,
课
号
,
成
绩
}
-
学号
→
{
姓
名
,
年
龄
}
学号\rightarrow \{姓名, 年龄\}
学
号
→
{
姓
名
,
年
龄
}
-
班号
→
班
长
班号\rightarrow 班长
班
号
→
班
长
-
{学
号
,
课
号
}
→
成
绩
\{学号, 课号\}\rightarrow 成绩
{
学
号
,
课
号
}
→
成
绩
例子2:
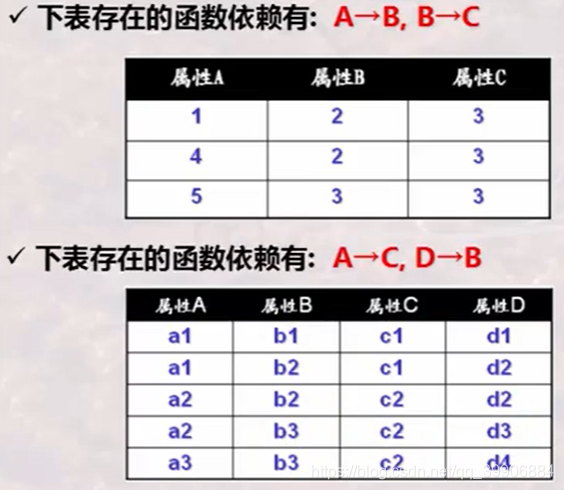
2. 函数依赖的特性
-
对
X→
Y
X\rightarrow Y
X
→
Y
,但
Y⊄
X
Y\not\subset X
Y
⊂
X
,则称
X→
Y
X\rightarrow Y
X
→
Y
为非平凡的函数依赖 -
若
X→
Y
X\rightarrow Y
X
→
Y
,则任意两个元组,若
XX
X
上值相等,则
YY
Y
上值必然相等,这样就称
XX
X
为决定因素 -
若
X→
Y
X\rightarrow Y
X
→
Y
,
Y→
X
Y\rightarrow X
Y
→
X
,则记作
X↔
Y
X\leftrightarrow Y
X
↔
Y
-
若
YY
Y
不函数依赖于
XX
X
,则记作
X↛
Y
X\not \rightarrow Y
X
→
Y
-
X→
Y
X\rightarrow Y
X
→
Y
,有基于模式
RR
R
的,则要求对任意的关系
rr
r
成立;有基于具体关系
rr
r
的,则要求某一关系
rr
r
成立 -
如一关系
rr
r
的某属性集
XX
X
,
rr
r
中根本没有
XX
X
上相等的两个元组存在,则
X→
Y
X\rightarrow Y
X
→
Y
恒成立
二. 部分或完全函数依赖
在
R
(
U
)
R(U)
R
(
U
)
中,若
X
→
Y
X\rightarrow Y
X
→
Y
并且对于
X
X
X
的任何真子集
X
′
X’
X
′
都有
X
′
↛
Y
X’ \not\rightarrow Y
X
′
→
Y
,则称
Y
Y
Y
完全函数依赖
于
X
X
X
,记为:
X
→
f
Y
X \rightarrow^f Y
X
→
f
Y
;
否则称
Y
Y
Y
部分函数依赖
于
X
X
X
,记为
X
→
p
Y
X \rightarrow^p Y
X
→
p
Y
部份依赖存在着非受控冗余
例子:

- 单独一个学号,单独一个课号都不能决定 U,只有一起才能决定 U,故为完全函数依赖
- 单独一个学号就可以决定姓名,所以是部分函数依赖
- 单独一个学号,单独一个课号都不能决定成绩,只有一起才能决定成绩,故为完全函数依赖
三. 传递函数依赖
在
R
(
U
)
R(U)
R
(
U
)
中,若
X
→
Y
X\rightarrow Y
X
→
Y
,
Y
→
Z
Y\rightarrow Z
Y
→
Z
,且
Y
⊄
X
Y\not \subset X
Y
⊂
X
,
Z
⊄
Y
Z\not \subset Y
Z
⊂
Y
,
Z
⊄
X
Z\not \subset X
Z
⊂
X
,
Y
↛
X
Y\not \rightarrow X
Y
→
X
,则称
Z
Z
Z
传递函数依赖于
X
X
X
传递依赖存在着非受控冗余
例子:

四. 函数依赖相关的几个重要概念
1. 候选键
设
K
K
K
为
R
(
U
)
R(U)
R
(
U
)
中的属性或者属性组合,若
K
K
K
完全函数依赖于
U
U
U
,则称
K
K
K
为
R
(
U
)
R(U)
R
(
U
)
上的
候选键
说明:
-
可任选一候选键作为
RR
R
的
主键
-
包含在任一候选键中的属性称作
主属性
,其他属性称作
非主属性
-
若
KK
K
是
RR
R
的一个候选键,
K⊂
S
K \subset S
K
⊂
S
,则称
SS
S
为
RR
R
的一个
超键
2. 外键
若
R
(
U
)
R(U)
R
(
U
)
中的属性或属性组合
X
X
X
并非
R
R
R
的候选键,但
X
X
X
却是另一关系的候选键,则称
X
X
X
为
R
R
R
的外键
3. 逻辑蕴涵
设
F
F
F
是关系模式
R
(
U
)
R(U)
R
(
U
)
中的一个函数依赖集合,
X
X
X
,
Y
Y
Y
是
R
R
R
的属性子集,如果从
F
F
F
中的函数依赖能够推导出
X
→
Y
X \rightarrow Y
X
→
Y
,则称
F
F
F
逻辑蕴涵
X
→
Y
X \rightarrow Y
X
→
Y
,或称
X
→
Y
X \rightarrow Y
X
→
Y
是
F
F
F
的
逻辑蕴涵
记作
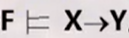
函数依赖有显性给出的,也有隐含的
说明:
-
设
FF
F
是关系模式
R(
U
)
R(U)
R
(
U
)
中的一个函数依赖集合,
X→
Y
X \rightarrow Y
X
→
Y
是一个函数依赖,若对
RR
R
中的每个满足
FF
F
的关系
rr
r
,能够用形式逻辑推理的方法推出
rr
r
也满足
X→
Y
X \rightarrow Y
X
→
Y
,则称
X→
Y
X \rightarrow Y
X
→
Y
是
FF
F
的
逻辑蕴涵
-
若满足
FF
F
的每个关系均满足
X→
Y
X \rightarrow Y
X
→
Y
,则说
FF
F
逻辑蕴涵
X→
Y
X \rightarrow Y
X
→
Y
4. 闭包(Closure)
被
F
F
F
逻辑蕴涵的所有函数依赖集合称为
F
F
F
的闭包,记作
F
+
F^+
F
+
说明:
-
若
F+
=
F
F^+ = F
F
+
=
F
,则说
FF
F
是一个
全函数依赖族(函数依赖完备集)
例子:

特点:
- 小集合,大闭包
- 包含了平凡的函数依赖
五. 关于函数依赖的公理和定理
1. Armstrong’s Axioms A1~A3
设
R
(
U
)
R(U)
R
(
U
)
是属性集
U
=
{
A
1
,
A
2
,
.
.
.
,
A
n
}
U=\{A_1, A_2,…,A_n\}
U
=
{
A
1
,
A
2
,
.
.
.
,
A
n
}
上的一个关系模式,
F
F
F
为
R
(
U
)
R(U)
R
(
U
)
的一组函数依赖,记为
R
(
U
,
F
)
R(U, F)
R
(
U
,
F
)
,则有如下规则成立:
-
[A1]
自反律:若
Y⊆
X
⊆
U
Y \subseteq X \subseteq U
Y
⊆
X
⊆
U
,则
X→
Y
X \rightarrow Y
X
→
Y
被
FF
F
逻辑蕴涵 -
[A2]
增广律:若
X→
Y
∈
F
X \rightarrow Y \in F
X
→
Y
∈
F
,且
Z⊆
U
Z \subseteq U
Z
⊆
U
,则
XZ
→
Y
Z
XZ \rightarrow YZ
X
Z
→
Y
Z
被
FF
F
逻辑蕴涵 -
[A3]
传递律:若
X→
Y
∈
F
X \rightarrow Y \in F
X
→
Y
∈
F
,且
Y→
Z
Y \rightarrow Z
Y
→
Z
,则
X→
Z
X \rightarrow Z
X
→
Z
被
FF
F
逻辑蕴涵
公理的作用
:由已知的函数依赖推导出隐含的函数依赖
3. Armstrong’s Axioms 引理1

2. Armstrong’s Axioms 引理2
-
合并律:若
X→
Y
X \rightarrow Y
X
→
Y
且
X→
Z
X \rightarrow Z
X
→
Z
,则
X→
Y
Z
X \rightarrow YZ
X
→
Y
Z
-
伪传递律:若
X→
Y
X \rightarrow Y
X
→
Y
且
WY
→
Z
WY \rightarrow Z
W
Y
→
Z
,则
XW
→
Z
XW \rightarrow Z
X
W
→
Z
-
分解律:若
X→
Y
X \rightarrow Y
X
→
Y
且
Z⊆
Y
Z \subseteq Y
Z
⊆
Y
,则
X→
Z
X \rightarrow Z
X
→
Z
证明:

3. 属性(集)闭包
对
R
(
U
,
F
)
,
X
⊆
U
,
U
=
{
A
1
,
A
2
,
.
.
.
,
A
n
}
R(U, F), X \subseteq U, U = \{A_1, A_2,…,A_n\}
R
(
U
,
F
)
,
X
⊆
U
,
U
=
{
A
1
,
A
2
,
.
.
.
,
A
n
}
,令:
X
F
+
=
{
A
i
∣
用
A
r
m
s
t
r
o
n
g
A
x
i
o
m
A
1
,
A
2
,
A
3
可
从
F
导
出
X
→
A
i
}
X^+_F = \{A_i | 用Armstrong\ Axiom\ A1,A2,A3可从 F 导出 X \rightarrow A_i\}
X
F
+
=
{
A
i
∣
用
A
r
m
s
t
r
o
n
g
A
x
i
o
m
A
1
,
A
2
,
A
3
可
从
F
导
出
X
→
A
i
}
则称
X
F
+
X^+_F
X
F
+
为关于
F
F
F
的
属性(集)闭包
注:显然
X
⊆
X
F
+
X\subseteq X^+_F
X
⊆
X
F
+
4. Armstrong’s Axioms 引理4
当且仅当
Y
⊆
X
F
+
Y\subseteq X^+_F
Y
⊆
X
F
+
时,
X
→
Y
X\rightarrow Y
X
→
Y
可从
F
F
F
由 Armstrong Axiom 导出
证明:

5. Armstrong Axiom A1,A2,A3 特性
- 有效性:通过公理推出的结论是正确的
-
完备性:被
FF
F
逻辑蕴涵的所有函数依赖都能由 A1,A2,A3 在
FF
F
的基础上推出
6. 覆盖
对
R
(
U
)
R(U)
R
(
U
)
上的两个函数依赖集合
F
,
G
F, G
F
,
G
,如果
F
+
=
G
+
F^+=G^+
F
+
=
G
+
,则称
F
F
F
和
G
G
G
是等价的,也称
F
F
F
覆盖
G
G
G
或者
G
G
G
覆盖
F
F
F
7. Armstrong’s Axioms 引理5
F
+
=
G
+
⟷
F
⊆
G
+
∧
G
⊆
F
+
F^+=G^+ \longleftrightarrow F\subseteq G^+ \wedge G\subseteq F^+
F
+
=
G
+
⟷
F
⊆
G
+
∧
G
⊆
F
+
8. Armstrong’s Axioms 引理6
每个函数依赖集
F
F
F
可被一个其右端至多有一个属性的函数依赖之集
G
G
G
覆盖
9. 最小覆盖
若
F
F
F
满足以下条件,则称
F
F
F
为
最小覆盖(Minimal Cover)
或
最小依赖集
:
- F 中每个函数依赖的右部是单个属性
-
对任何
X→
A
∈
F
X\rightarrow A \in F
X
→
A
∈
F
,有
F−
{
X
→
A
}
F-\{X \rightarrow A\}
F
−
{
X
→
A
}
不等价于
FF
F
-
对任何
X→
A
∈
F
,
Z
⊂
X
X\rightarrow A \in F, Z\subset X
X
→
A
∈
F
,
Z
⊂
X
,有
(F
−
{
X
→
A
}
)
⋃
{
Z
→
A
}
(F-\{X \rightarrow A\})\bigcup \{Z \rightarrow A\}
(
F
−
{
X
→
A
}
)
⋃
{
Z
→
A
}
不等价于
FF
F
[定理]:
-
每个函数依赖集
FF
F
都有等价的最小覆盖
F′
F’
F
′