前言
本篇旨在介绍关于数据结构的一些入门的知识点,让大家能够更好的入门数据结构与算法,故此都是对一些简单数据结构与基本算法的梳理
一、复杂度
虽然说数据结构和算法是两个不同的大小,那为什么先介绍复杂度呢?
Pascal
之父——Nicklaus Wirth曾提出一句名言:程序 = 数据结构 + 算法
由此便可看出了数据结构与算法之间密不可分的联系在解决问题的过程中,
数据结构
要配合
算法
选择最优的存储结构来存储数据,而算法也要结合数据存储的特点,用最优的策略来分析并处理数据,由此可以
最高效地解决问题
。
(1)时间复杂度
时间复杂度计算的是算法中,
基本操作执行的次数
,而
并非程序运行的时间长短
等
例子:
请计算一下Func1基本操作执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
for (int j = 0; j < N ; ++ j)
++count;
for (int k = 0; k < 2 * N ; ++ k)
++count;
int M = 10;
while (M--)
++count;
printf("%d\n", count);
}
解答:
我们很容易计算出,一共执行的次数F(N) = N^2 + 2*N + 10,但是在实际计算时间复杂度时我们只需要计算出大概执行的次数即可。故此我们这里使用到一个大O的渐进表示法:
大O表示法
大O符号:是用于描述函数渐进行为的数学符号。
(1)用
常数1取代所有的常数
(2)计算出的复杂度表达式中
只保留其最高阶项
(3)如果最高阶项存在,且其系数不是1,则
去除与这个项相乘的系数
(即项数默认为1)
所以在这里使用了大O的渐进表示法后,其时间复杂度则为
O(N^2)
知道了大O表示法后我们再来看一个例子:
计算我们都学过的一个简单算法:BinarySearch(二分查找)的时间复杂度
如果不知道该算法,可以先去了解一下
二分查找
int BinarySearch(int* a, int n, int x)
{
int begin = 0;
int end = n;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1; //未找到则返回-1
}
解答:
最好的情况下,第一次二分便找到了目标数值,则该程序只执行了一次运算;
最坏的情况下呢,则是没有找到,那找了多少次呢?
每次查找都是将查找区域一分为二,我们设整个区域范围为N,那每查找一次都是N / 2,当
N / 2 / 2 / 2… / 2 = 1
时,若还没有找到,则在该区域里不存在该数值。所以我们可以知道N除了几次2,就是查找了多少次。设查找了n次,故综合上面的式子可得:N/2^n = 1,化简得 2^n = N,则解方程得:n = logN
tips:
logN
在算法分析
中表示是底数为
2
,对数为
N
。有些地方会写成
lgN
主要是因为因为2这个底数在计算机上不好敲出来
所以最坏的情况下则执行次数为logN次,因为在现实情况下,情况时比较复杂的,所以计算时间复杂度时,都只会计算
最坏情况下
的时间复杂度。所以
二分查找的时间复杂度就是O(logN)
。
时间复杂度对比:
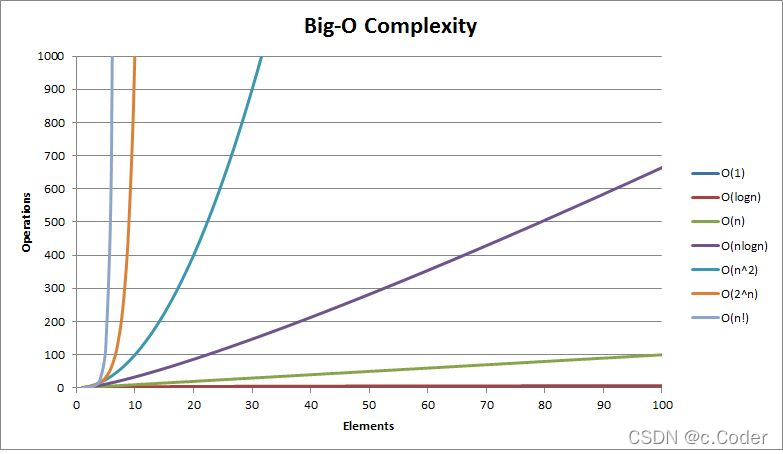
(2)空间复杂度
空间复杂度计算的是临时开辟的辅助空间的大小,即
临时占用
存储空间的变量的个数
空间复杂度也是使用大O表示法
例子:
计算冒泡排序的空间复杂度
void BubbleSort(int* a, int n)
{
for (int end = n; end > 0; --end)
{
int exchange = 0;
for (int i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (!exchange)
break;
}
}
解答:
由于大O表示法,冒泡排序里创建的临时变量都为
常数个
,故此空间复杂度为O(1)
再来计算一道:
计算Fibonacci的空间复杂度
long long* Fibonacci(size_t n) {
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
解答:
程序里动态开辟了n+1个
临时变量
空间,故此空间复杂度为O(N)
二、基础数据结构
线性表
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的
tips:用编程语言实现线性表时,增删查改都先考虑普适情况,最后再考虑极端情况
1、顺序表(vector;deque)
顺序表分为动态顺序表与静态顺序表,其逻辑结构和物理结构(存储结构)上都是连续的
静态顺序表即为
普通数组
;动态顺序表即用动态开辟的内存作为存储空间的数组
顺序表的优缺点:
优点:支持随机访问
缺点:空间容易浪费、头插效率低、删除数据的效率低等(故由此引出了链表)
2、链表(list)
链接跳转:
一篇文章详细了解单链表
链接跳转:
一篇文章详细了解双向带头链表
链表在逻辑结构上是连续的,物理结构上则为
非连续
的
链表也分为静态与动态链表(静态链表如今已经不常用)
链表大体有
带头/不带头
、
循环/不循环
和
单向/双向
这三大类
其互相组合共有八种类型的链表
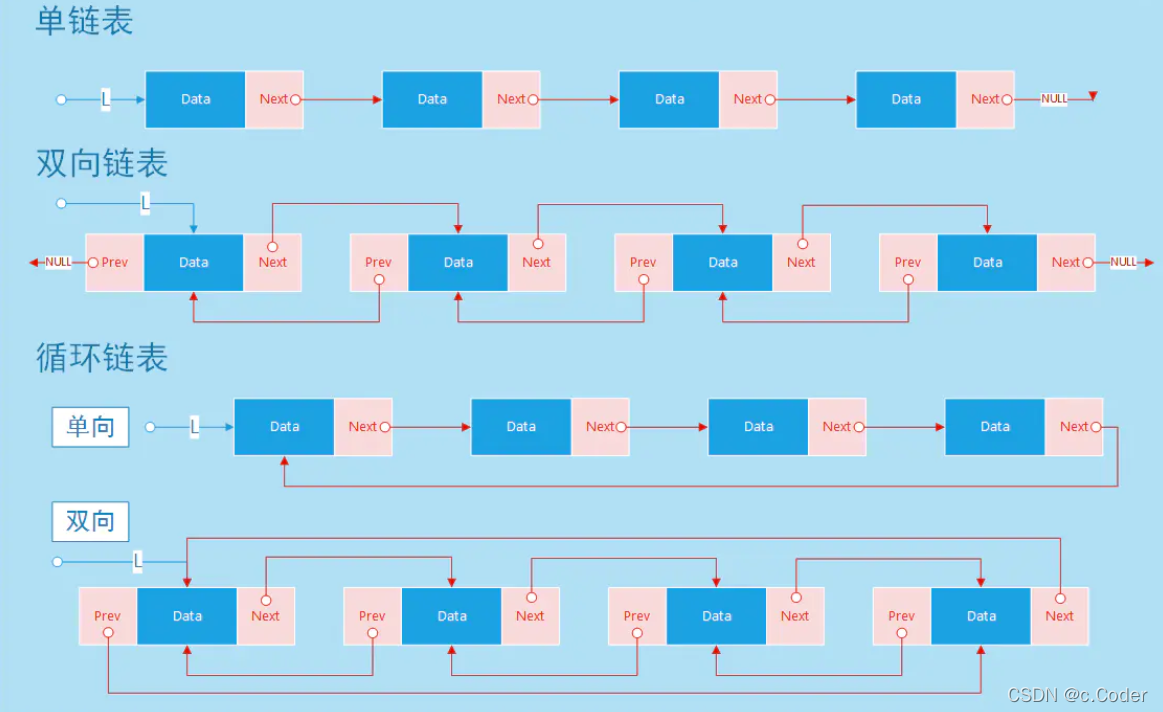
主要掌握了
无头单向不循环链表
与
带头双向循环链表
即可明晰其它类型的链表的实现方式
链表
本质
就是数据元素之间
通过指针相互链接
了起来(故每个结点分为了数据域和指针域)
tips:实现时注意避免空指针的问题
链表的优缺点:
优点:任意位置插入数据的时间复杂度为O(1);没有增容操作,按需所取
缺点:不支持随机访问
3、栈(stack)
链接跳转:
一篇文章充分了解栈
栈为一种特殊的线性表,只允许在一端进行数据的插入和删除数的操作
特点:
先进后出
(出入数据都在栈顶)LIFO(last infirst out)
插入数据的操作即被称作入栈(压栈),删除数据的操作被称作出栈。
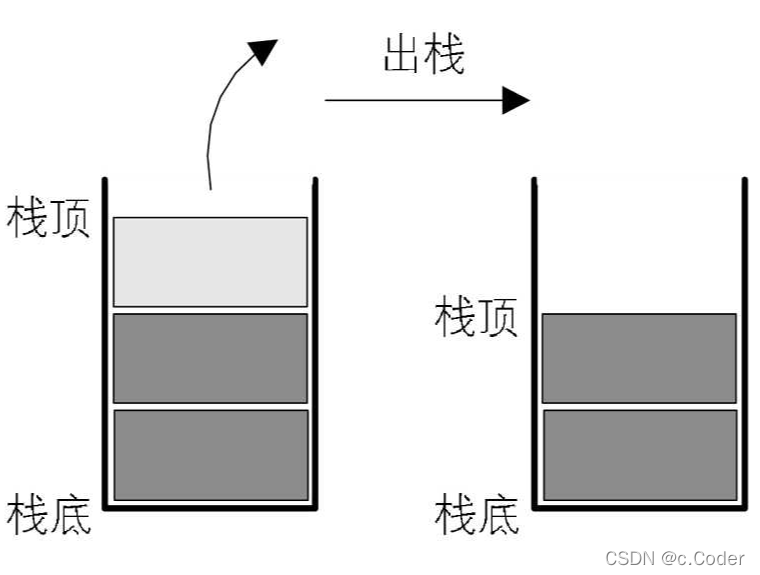
实现栈可以使用数组/链表都行(按需灵活使用):
1、数组的首位做栈底,尾部做栈顶,入数据即等同于尾插数据,出数据即等于尾删数据
数组比较合适,唯一缺陷就是要增容2、链表的话,单链表如果是链表尾作栈顶,尾删效率比较低,所以建议使用双向带头循环链表,如果要用单链表,则使用链表头作栈顶即可
4、队列(queue)
链接跳转:
一篇文章充分了解队列
一种特殊的线性表,只允许
在队尾入数据,队头出数据
特点:
先进先出
FIFO(first in first out)实现队列一样可以考虑使用数组/链表
1、数组实现时,队头出数据的效率比较低下,所以建议使用单链表2、单链表进行出数据即是头删,入数据即是尾插,出数据时,即头删
tip:
1、只有一个结点时要注意删除完后,尾指针可能成为野指针的问题,不然下一次再插入数据时则会导致内存非法访问的错误
2、用个结构体记录队列的头指针和尾指针,可以简化操作
5、串(string)
串( string)是由零个或多个字符组成的有限序列,又名叫字符串。
一般表示为 str = ”
”
涉及的一些概念:
空串:
当n=0时的串称为空串。
空格串:
只包含空格的串。
(空格串包含n个空格,是有长度的,而空串是没有长度的)
子串与主串:
串中任意个数的连续字符组成的
子序列
称为该串的子串。相应地,包含子串的串称为主串。关于串,更多要了解的是
模式匹配算法
非线性表
数据元素之间存在一对多或者多对多的关系
树
主要学习的是二叉树相关的知识点
定义:
树由
n(n≥0
)个有限节点组成一个具有层次关系的集合树的特点:
子树之间是不相交的,每个节点有且仅有一个父节点
一棵N个节点的树有N-1条边。如下:
tips:树的结构本身就是一个递归结构:
根 子树…
子树又分为
根 子树…
所以解决树的相关问题时都是利用
分治算法(递归)
来解决
关于树的一些名词概念
节点的度:
一个节点含有的子树的个数即为该结点的度
树的度:
一棵树中,最大的节点的度称为该树的度
叶子节点:
度为0的结点(终端结点)
子节点:
一个节点含有的子树的根节点称为该结点的子节点
父节点:
若一个节点含有子节点,则这个节点称为其子结点的父节点
兄弟节点:
具有相同的父节点的节点互称为兄弟节点
节点的层次:
从根开始定义,根为第一层,根的子节点为第二层,以此类推
树的高度:
即树中结点的最大层次
二叉树:
每个节点最多只有两个子树(即二叉树不存在度大于2的节点)
二叉树的子树有左右之分,且顺序不能颠倒
关于二叉树的一些名词概念
满二叉树:
每一层都是满的(每一层的度都为2)
满二叉树是一种特殊的完全二叉树(完全且满的二叉树)
完全二叉树:
除了最后一层不满之外,上面每一层都是满的(前h-1层都是满的),
但是最后一层从左往右的节点都是连续的
搜索二叉树:
任何一棵树,左子树都比根要小,右子树都比根要大;
AVL树即平衡搜索树,左右子树趋于平衡,高度相差不大于1
快速构建
普通二叉树
的简单方式:
即先将二叉树的结点结构(struct)写出来
然后再把每一个结点malloc出来后,再手动将其按二叉树的结构依次链接起来即可
关于二叉树的一些特殊性质
假设一棵满二叉树的高度为h,
第一层的节点数为2^0,第二层的节点数为2^1,第三层的节点数为2^2…,
总节点的个数即2^0 + 2^1 + 2^2 + … +2^(h-1) = N
依等比数列求和公式可得:
N = 2^h – 1
—>
h= log(N+1)
对于任何一棵二叉树,设
度为0的叶子结点的个数为n0,度为2的结点的个数为n2
,
则有
n0 = n2 + 1
(叶子结点的个数比度为2的结点的个数多一个)
关于二叉树的遍历
任何一棵二叉树都要分为三个部分:
根节点,左子树,右子树
子树也是相同的结构,也要分为根节点,左子树和右子树
以此类推…分到空树为止(分割到不可分割的部分)
深度优先遍历
递归进行的遍历,主要利用到分治算法,以递归解决问题
(通过前序/后序 + 中序遍历的结果可以还原一整棵二叉树)
前序遍历(先根遍历)
即先访问根,再访问左子树,再访问右子树
访问左子树时,左子树也是一棵二叉树,即也跟原来问题的规模类似,所以也是先访问根,再访问左子树,再访问右子树,以此类推,直到访问到叶子结点的子节点(左子树为空,右子树为空),即访问到的根为空了就返回
中序遍历(中根遍历)
即先访问左子树,再访问根,再访问右子树
后序遍历(后根遍历)
先访问左子树,再访问右子树,最后访问根
访问过程都与前序类似,也是要不断分割至不能分割的子问题为止
广度优先便利
非递归进行的遍历
核心思路:利用队列先进先出的特性进行遍历,关键就是上一层数据带下一层数据
层序遍历
思路:先将根入队列,然后队列不为空则将队头数据取出来,同时判断左子树和右子树(根节点)是否为空,若不为空,则将对应节点依次(左子树,右子树)入队列,依次进行即将每一层依次遍历了一遍。
树的表示方式
1、左孩子右兄弟表示法
无论有几个孩子,每个只有两个指针
一个保存第一个孩子,一个保存其右边的兄弟
2、双亲表示法
用数组表示,数组里只存父节点的下标。
3、二叉树的表示方式
二叉链 or 三叉链
二叉链:两个节点,分别指向其左孩子和右孩子
三叉链:三个节点,分别指向左孩子,右孩子和父节点
写在最后
本篇主要介绍了最基础的入门数据结构,如果对你有帮助可以点赞转发让更多的人看到~