常用的概率统计知识
一、随机事件
本文为在学习概率统计中,进行的汇总
1.基本概念
在一定条件下,在个别试验或观察中呈现不确定性,但在大量重复试验或观察中其结果又具有一定规律性的现象,称为随机现象。
使随机现象得以实现和对它观察的全过程称为随机试验,记为E。
关于几个基础概念,以最常见的掷骰子为例进行说明:
-
随机试验的所有可能结果组成的集合为
样本空间
,记为Ω:如Ω = {1,2,3,4,5,6}; -
试验的每一个可能结果称为
样本点
,记为ω:如ω1 = {1},ω2 = {2},ω3 = {3}; -
样本空间Ω中满足一定条件的子集为
随机事件
,用大写字母A、B、C…表示。(随机事件在随机试验中可能出现也可能不出现):如A = {1,2,3}; -
;在试验中,一个事件发生是指构成该事件的一个样本点出现,由于样本空间Ω包含了所有的样本点,所以在每次试验中,它总是发生,因此称Ω为
必然事件
; -
空集φ不包含任何样本点,且在每次试验中总不发生,所以是
不可能事件
:如掷骰子出现的点数为7。
2.概率
事件A发生的几率。
同样以掷骰子为例,1,2,3,4,5,6出现的概率均为1/6,我们令A = {1,2},B = {1,2,3},根据性质则有
-
对于任一事件A,均有P(~A) = 1 – P(A)
P(~A) = 1 – P(A) = 1 – 1/3 = 2/3 -
对于两个事件A和B,若A∈B,则有P(B – A) = P(B) – P(A),P(B) > P(A)
P(B – A) = P(B) – P(A) = 1/2 – 1/3 = 1/6 -
对于任意两个事件A和B,有P(A∪B) = P(A) + P(B) – P(A ∩ B)
P(A∪B) = P(A) + P(B) – P(A ∩ B) = 1/3 + 1/2 -1/3 = 1/2
3.古典概型
首先需要复习一下排列组合的计算公式:
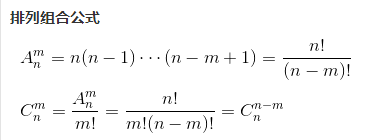
-
定义
设随机事件E的样本空间中只有有限个样本点,即Ω = {ω₁,ω₂…},其中n为样本点的总数,每个样本点出现的概率是相等的,并且每次试验有且仅有一个样本点发生,则称这类现象为古典概型。 -
举例
假设有n个不同颜色的球,每个球以同样的概率1/m落到m个格子(m >= n)中,且每个格子可以容纳任意多个球,分别求出如下两个事件A和B的概率。A:指定的n个格子中各有一个球;
由于每个球可以平均地落入m个格子中的任一个,并且每一个格子中可落入任意多个球,所以n个球落入m个格子中的分布情况相当于从m个格子中选取n个的可重复排列,故样本空间共有mⁿ种可能的基本结果,所以事件A所含基本结果数是n个球在指定的m个格子中的全排列数,即:
P(A) = n!/ mⁿB:存在k个格子,其中各有一个球;
由于m个格子是可以任意选取的,故先从m个格子中任意选出n个来,那么选法共有C(m,n)种,对于每种选定的n个格子,有n!个几本结果,则有
P(B) = C(m,n)* n!/ mⁿ = n!/ (mⁿ * (m – n)!) -
Python实现
将上述例子应用到具体的问题中,概率论的历史上有一个颇为著名的生日问题:求n个同班同学没有两人生日相同的概率。
如果把这n个同学看作上例中的n个球,而把一年365天看作格子,即m = 365,则上述的P(B)就是我们要求的概率,令n = 40。
用Python实现古典概率的计算