一、 K近邻
KNN算法的基本思想就是在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,其算法的描述为:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
其中在计算距离时采用欧氏距离或曼哈顿距离:

k值的选择:当k值较小时,预测结果对近邻的实例点非常敏感,容易发生过拟合;如果k值过大模型会倾向大类,容易欠拟合;通常k是不大于20的整数
优点:精度高,对异常值不敏感
缺点:k值敏感,空间复杂度高(需要保存全部数据),时间复杂度高(平均O(logM),M是训练集样本数)
二、感知机
PLA全称是Perceptron Linear Algorithm,即线性感知机算法,属于一种最简单的感知机(Perceptron)模型。它是支持向量机和神经网络的基础。感知机模型是机器学习二分类问题中的一个非常简单的模型。它的基本结构如下图所示:
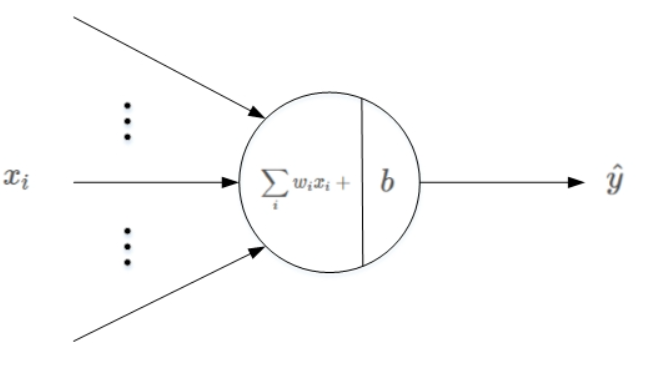
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练数据集正实例点和负实例点完全正确分开的分离超平面。如果是非线性可分的数据,则最后无法获得超平面。
所以感知机的目标函数为一条直线或者一个超平面,其输出为:
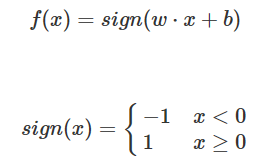
其中wx+b表示空间中的一点的坐标,我们的目标取找到合适的w和b,使得f(x)和真实的y值相符合,当然不可能达到完全符合,所以应当是尽可能多的点被正确分类。换句话说
就是让那些分错类的点越接近边界线越好。这时我们就可以用距离来定义损失函数了:损失值=错误的点到边界的距离的总和。优化的对象便是让这个距离之和最小。
由点到平面的距离公式我们可以得到任意一点距离我们上面定义的模型的距离为:
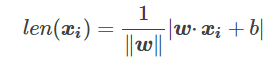
有了计算距离的方式,我们来看看损失函数究竟怎么定义。这里需要注意的是我们的目标是那些分错类的点,而不是所有点,因此不能直接将距离作为损失函数,所以我们需要找出那些分错类的点,建立他们的损失函数。这里正好可以利用绝对值来进行区分正确点和错误点。对于模型来说,在分类错误的情况下,若
w
⋅
xi
+
b
>0,去掉绝对值不变,则实际的
yi
应该是等于-1,为了使原式保持正值,则添加一个负号。而当
w
⋅
xi
+
b
<0时,去掉绝对值加负号,此时
yi
等于1,上式为正值。因此由这个特性我们可以去掉上面的绝对值符号,将公式转化为:
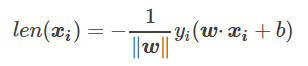
去掉||w||后得到最终的损失函数为:
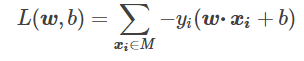
这里求最小值采用的是随机梯度下降算法,因为我们每次取一个点来判断他是不是错误点,然后才能带入优化。
三、支持向量机SVM
支持向量机与感知机相似。他的目的也是取寻找一条直线或一个超平面将数据进行二分类。只不过感知机的原理是到边界的距离最小,而SVM的原理则是“间隔最大化”。
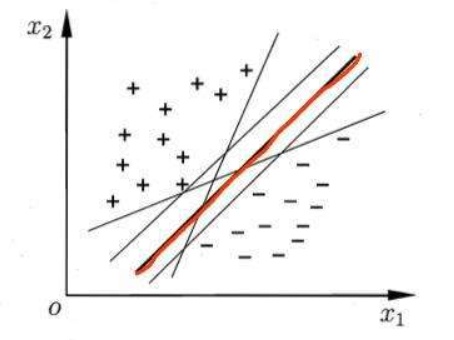
从上图可以看出,如果数据集线性可分,那么这样的直线又无数条,但是我们的目标是找到一条容忍度最好的直线,即黄色的那条。
-
为什么要间隔最大呢?
一般来说,
一个点距离分离超平面的远近可以表示分类预测的确信度,如图中的A B两个样本点,B点被预测为正类的确信度要大于A点,所以SVM的目标是寻找一个超平面,使得离超平面较近的异类点之间能有更大的间隔,即不必考虑所有样本点,只需让求得的超平面使得离它近的点间隔最大
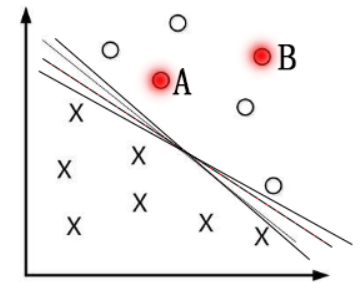
2. 怎么计算间隔
f
(
x
)=
wTx
+
b
表示空间中一点的坐标。当
f
(
x
) 等于0的时候,x便是位于超平面上的点,而
f
(
x
) 大于0的点对应 y=1 的数据点,
f
(
x
)小于0的点对应y=-1的点。这里的y=1和-1都是可以随意指定的,相当于两种label,为了方便计算就取1和-1了。
根据上述原理我们可以总结为一个表达式:
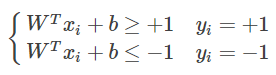
实际上该公式等价于
yi
(
WTxi
+
b
)≥ +1。这就是最大间隔假设
3. 什么是支持向量
距离超平面最近的这几个样本点满足
yi
(
WTxi
+
b
)=1,它们被称为“支持向量”。
虚线称为边界,两条虚线间的距离称为
间隔(margin)
。
所谓的支持向量,就是使得上式等号成立,即最靠近两条虚边界线的向量。如果
WTxi
+
b
>1,那就说明更加支持了。
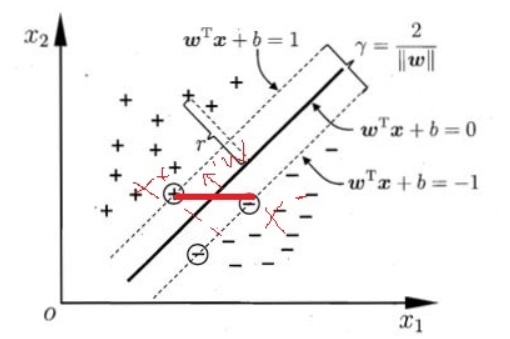
所以我们在计算最大间隔的时候,其实关注的是支持向量到超平面的距离。

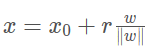
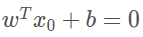
由上述两式联立可得
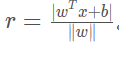
对于支持向量,
WTxi
+
b=1或-1,所以最大间隔变为:
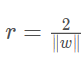
这样我们们便确定了目标函数
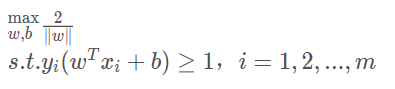
等价于:
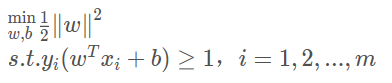
SVM函数的求解属于凸二次规划问题,采用拉格朗日乘数法求解。添加拉格朗日乘子 αi≥0,则整个拉格朗日函数可写成:
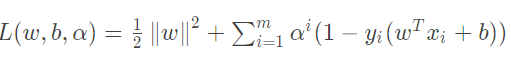
4. 非线性支持向量机与核函数技
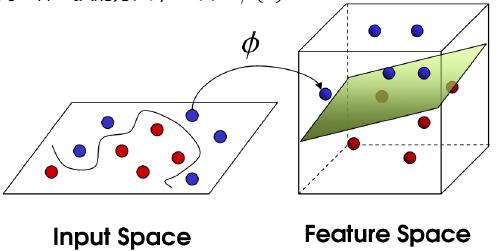
对于非线性分类问题,显然无法用一个线性分离超平面来把不同的类别的数据点分开,那么可以用以下思路解决这个问题:
-
首先使用一个变换
z
=
ϕ
(
x
)将非线性特征空间x映射到新的线性特征空间z
-
在新的z特征空间里使用线性SVM学习分类的方法从训练数据中学习分类模型
但是,这里有一个问题: ϕ(xi)⋅ϕ(xj)计算起来要分两步,先映射x到z空间,然后在z空间(一般是较高维度)作高维度的內积zi⋅zj。
为了简化这个运算过程,如果我们找到一个核函数K(xi,xj), 即K是关于x的函数,其运算在低维空间上进行,然后使得K(xi,xj)=ϕ(xi)⋅ϕ(xj),那么只需要计算一个比较好计算的核函数K(xi,xj),就可以避免先映射,再在高维空间內积的复杂运算。
常见的核函数有:
二次多项式核、高斯核
5. 软间隔
我们一直假设训练样本在样本空间或特征空间食线性可分的,即存在一个超平面能将不同类的样本完全划分开。然而,在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分;退一步说,
即便恰好找到了某个核函数使训练样本在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合造成的
。
缓解该问题的一个方法是允许支持向量机在一些样本上出错,为此要引入“软间隔”的概念。
当然我们还要限制这些分错的样本个数应当越少越好
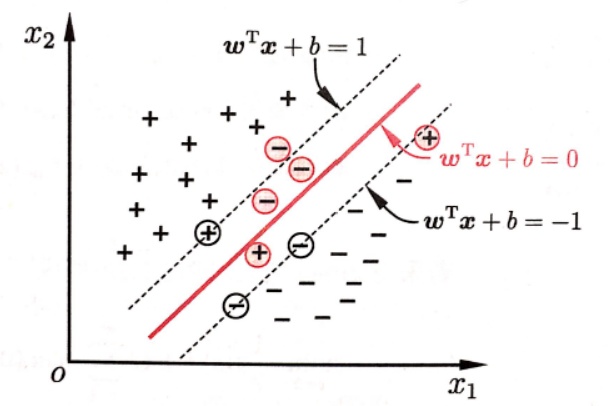
之前做了一个最大间隔的假设,即所有样本都满足:
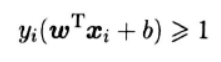
也就是说所有的样本都得被分对,这称之为“硬间隔”,而软间隔则允许某些样本不满足约束条件,于是,目标函数可写为
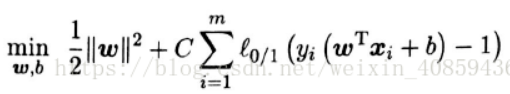
其中C是常数,L0/1是0/1的损失函数:
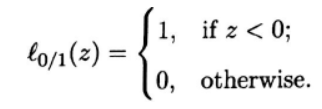
当C越大,模型的容忍程度就越小,边界越瘦,C越小,边界越胖,越多的样本被分错,所以C为无穷大时迫使所有样本都得满足约束
直接使用0/1的损失函数求解不好求,一般都是将其变为hinge损失函数:
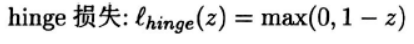
此时,我们的优化目标函数也就变成了:
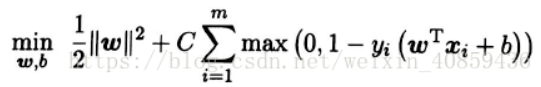
引入一个变量ξn=1− yi(Wx+b),我们成为“松弛因子”,如果yi(Wx+b)<1,带入hinge损失中,损失值大于0,说明样本被分错,因此ξn代表犯了多少错。优化的目标函数最终变为:
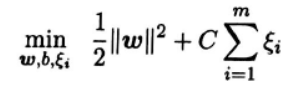
5. LR和SVM不同点
-
LR采用log损失,SVM采用合页(hinge)损失
逻辑回归方法基于概率理论,假设样本为1的概率可以用sigmoid函数来表示,然后通过
极大似然估计
的方法估计出参数的值(基于统计的,其损失函数是人为设定的凸函数) 。支持向量机基于几何
间隔最大化
原理,认为存在最大几何间隔的分类面为最优分类面.(有严格的推导)
-
LR对异常值敏感,SVM对异常值不敏感
支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用,虽然作用会相对小一些)。LR模型找到的那个超平面,是尽量让所有点都远离他,而SVM寻找的那个超平面,是只让最靠近中间分割线的那些点尽量远离,即只用到那些支持向量的样本。
-
对非线性问题的处理方式不同
LR主要靠特征构造,必须组合交叉特征,特征离散化。SVM也可以这样,还可以通过kernel(因为只有支持向量参与核计算,计算复杂度不高)。
(由于可以利用核函数,。SVM则可以通过对偶求解高效处理。LR则在特征空间维度很高时,表现较差。)
-
正则化不同
SVM的损失函数就自带正则(损失函数中的1/2||w||^2项),这就是为什么SVM是结构风险最小化算法的原因,而LR必须另外在损失函数上添加正则项