首先我们先明确什么时候需要用到回溯法:
回溯法:一种通过穷举所有可能情况来找所有解的算法,当发现候选的解不是可行解的时候,回溯就是把它舍弃。回溯法最为一种算法思想,它和递归函数还是有本质区别的。当你在思考一个问题的时候,发现你需要不断的穷举其所有的可能性。
一般回溯问题有三种(
负雪明珠
):
1. 有没有解
2. 求所有解
2.1 求所有解的个数
2.2 求所有解的具体信息
3. 求最优解
递归和回溯最大的不同在于,一般递归函数只要问题的最后的一个解,通常表现在有明确的数学公式。而回溯法则需要尝试解出问题的所有可能性,再根据问题的条件筛选不符合的所有解。当我们确定问题是用回溯法的时候,分析问题可以用画树的方式。举个简单的例子:Leetcode上的第22题——括号生成。“数字n代表生成括号的对数,请设计一个函数,用于生成所有可能的并且有效的括号”
输入:n = 3
输出:["((()))", "(()())", "(())()", "()(())", "()()()"]
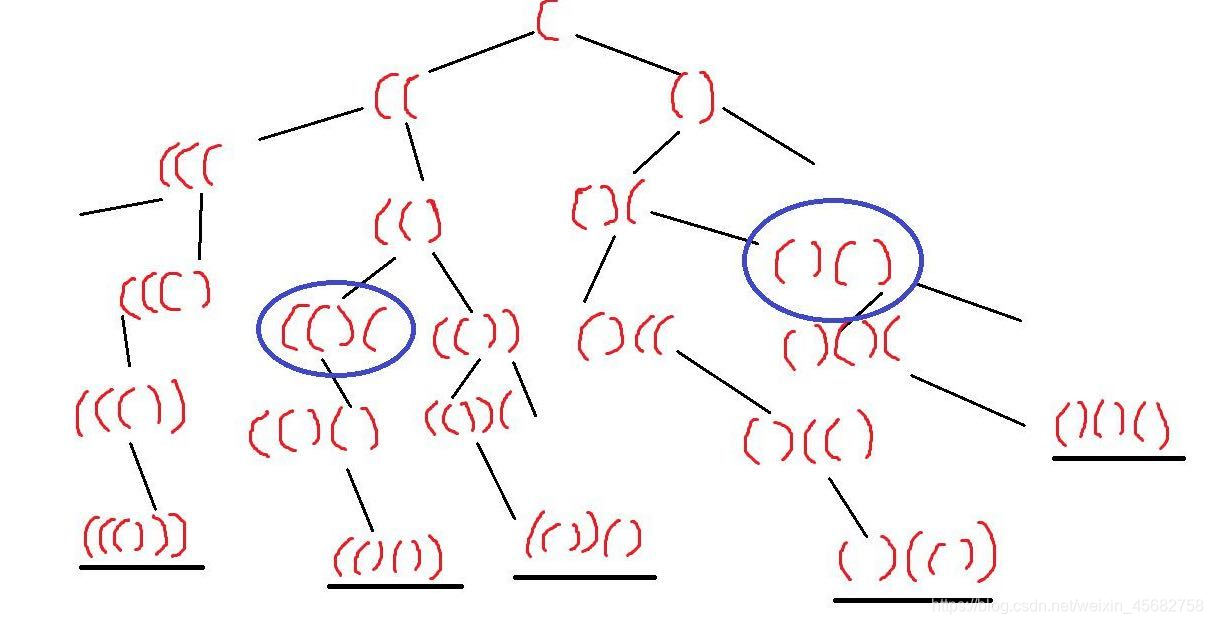
根据图中的树形结构我们找出如何用代码一步步实现。我们知道无论对于递归函数还是回溯,都要一个边界条件,对于这个问题的边界条件作用是对穷举过程中满足条件要求的“有效括号”添加到列表里。所以这里我们知道当n = 4时,边界条件为:
# S 是存放穷举所有可能性的列表 S = "(","(",(","(",")",")",")",")"
if len(S) == 2*n:
lis.append(''.join(S)) # jion()函数是把括号里列表的元素重新用符号''组合成一个元素
# 比如列表 S = ['(',')'] jion函数之后是 s = ['()']图中画黑线的是满足”有效括号“,把满足边界条件的括号,加入列表lis。
接下来我们在来分析穷举所有可能的括号组合。我们按照树的分叉路径来看,首先向括号S添加一个左括号”(“,然后再需要思考在什么条件下添加左括号呢?没错!添加的左括号的数量(用 left 参数表示)小于n = 4。看代码:
if left < n:
S.append('(')
backTrack(S, left+1, right) # left 左括号数量,right 右括号数量右括号的添加必须等到左括号添加了,才能组成’有效括号‘。所有右括号的添加条件right 小于 left。
if right < left:
S.append(')')
backTrack(S, left, right+1)
完整代码:
class Solution:
def get_ass(self, n):
lis = []
def backTrack(S, left, right):
if len(S) == 2*n:
lis.append(''.join(S))
return
if left < n:
S.append('(')
backTrack(S, left+1, right)
S.pop()
if right < left:
S.append(')')
backTrack(S, left, right+1)
S.pop() # S.pop()每次调用回溯函数之后删除最后一个元素
backTrack([], 0, 0)
return lis
# 如果在这看不明白pop()函数的作用可以试着在程序运行的自己研究一下,看不懂没有关系,多看看图结合程序,慢慢体会。