SINS/DR组合导航(一)

1.1 关于SINS/DR组合导航

SINS/DR组合导航是一种很常见的，也是很传统的一种组合导航方式，这里的DR叫做航位推算，定义是利用姿态、航向和行驶里程信息来推算机器人相对于起始点的相对位置。对于移动机器人来说，里程计可以是车轮里程计，或者视觉里程计；对于空中机器人来说，像对于军用直升机来说，可能是多普勒雷达；对于水下机器人来说，用的最多的就是多普勒计程仪（DVL）了。所以下文我采用一种广义上的里程计定义，这种里程计能够测量得到载体坐标系上的三维速度信息。

这里我主要基于严恭敏老师提出的轨迹相似性原理去补偿SINS/DR组合导航中的若干主要误差，像SINS和里程计之间的安误差，DVL刻度因子等误差。在轨迹相似性原理的推导过程中，能看出该算法的适用条件，然后会给出轨迹相似性原理的工程应用，最后的组合导航效果。

1.2 适用场景

下文要讨论的SINS/DR组合导航算法适用的场景主要特点如下：

1.俯仰，滚转角变化较小，或者可以理解为机器人近似在一个二维平面内运动，像无人船，或者仓库AGV,这一假设是完全成立的；

2.使用低成本惯导：像无人车，低速移动机器人使用的惯导，从量产角度考虑，用的也是不到万元的MEMS惯导产品。

1.3 SINS/DR组合导航主要误差项

这里可以先摆上些结论，对整个系统的理解很有帮助，就是以上场景下的SINS/DR组合导航，从速度误差方程和位置误差方程可以分析得到，惯导和里程计之间的偏航角，以及DVL刻度因子对组合导航精度影响较大，惯导和里程计之间的俯仰角主要影响高度漂移，在二维状态下可以忽略，惯导和里程计之间的滚转角不影响组合导航精度。

所以能够在线估计出这些主要的误差项，或者能够准确标定出这些误差项，对于SINS/DR组合导航精度有很大的提升。在线估计的方法主要是基于卡尔曼滤波，优点是可以实现一种自适应，即使参数发生变化，也不受影响，缺点算法复杂，估计精度和惯导的精度有关；标定方法的优点是利用一些优化算法可以实现比较精准的标定，缺点是当参数变化时，例如惯导的拆装，参数要重新标定，不太方便。

1.4 轨迹相似性原理

1.4.1 航位推算速度误差方程

设惯导坐标系为

b

$b$

系，车体坐标系为

m

$m$

系，假设从

m

$m$

到

b

$b$

系存在小量的安装偏差角，绕机器人

X

$X$

轴

o x_{m}

$o x_{m}$

、

Y

$Y$

轴

o y_{m}

$o y_{m}$

及

Z

$Z$

轴

o z_{m}

$o z_{m}$

分别存在俯仰偏角

\alpha_{\theta}

$α_{θ}$

，滚动偏角

\alpha_{\gamma}

$α_{γ}$

和方位偏角

\alpha_{\psi}

$α_{ψ}$

，机器人

X, Y, Z

$X, Y, Z$

轴分别对应右、前，上。记偏差角矢量

[

]

\alpha=\left[\begin{array}{lll} \alpha_{\theta} & \alpha_{\gamma} & \alpha_{\psi} \end{array}\right]^{\mathrm{T}}

$α = [α_{θ} α_{γ} α_{ψ}]^{T}$

，可得到如下公式：

(

)

[

−

]

C_{b}^{m}=I+(\alpha \times)=\left[\begin{array}{ccc} 1 & -\alpha_{\psi} & \alpha_{\gamma} \\ \alpha_{\psi} & 1 & -\alpha_{\theta} \\ -\alpha_{\gamma} & \alpha_{\theta} & 1 \end{array}\right]

$C_{b}^{m} = I + (α \times) = ⎣ ⎡ 1 α_{ψ} - α_{γ} - α_{ψ} 1 α_{θ} α_{γ} - α_{θ} 1 ⎦ ⎤$

另外，里程计的测量中还可能存在刻度系数误差

\delta K_{D}

$δ K_{D}$

，其输出速度大小

\tilde{v}_{D}

$\tilde{v}_{D}$

与理论速度大小

\mathcal{U}_{D}

$U_{D}$

之间的关系为：

(

)

\tilde{v}_{D}^{m}=\left(1+\delta K_{D}\right) v_{D}^{m}

$\tilde{v}_{D}^{m} = (1 + δ K_{D}) v_{D}^{m}$

所以，在导航坐标系中里程计的实际速度输出应该为：

(

)

(

−

)

(

−

)

(

)

≈

\tilde{v}_{D}^{n}=\tilde{C}_{b}^{n}\left(C_{b}^{m}\right)^{\mathrm{T}} \tilde{v}_{D}^{m}=\left(I-\phi_{D} \times\right) C_{b}^{n}(I-\alpha \times)\left(1+\delta K_{D}\right) v_{D}^{m} \approx

$\tilde{v}_{D}^{n} = \tilde{C}_{b}^{n} (C_{b}^{m})^{T} \tilde{v}_{D}^{m} = (I - ϕ_{D} \times) C_{b}^{n} (I - α \times) (1 + δ K_{D}) v_{D}^{m} \approx$

−

(

)

−

(

)

v_{D}^{n}-\left(\phi_{D} \times\right) C_{b}^{n} v_{D}^{m}-C_{b}^{n}(\alpha \times) v_{D}^{m}+C_{b}^{n} \delta K_{D} v_{D}^{m}=

$v_{D}^{n} - (ϕ_{D} \times) C_{b}^{n} v_{D}^{m} - C_{b}^{n} (α \times) v_{D}^{m} + C_{b}^{n} δ K_{D} v_{D}^{m} =$

(

)

v_{D}^{n}+v_{D}^{n} \times \phi_{D}+C_{b}^{n}\left(v_{D}^{m} \times\right) \alpha+C_{b}^{n} v_{D}^{m} \delta K_{D}

$v_{D}^{n} + v_{D}^{n} \times ϕ_{D} + C_{b}^{n} (v_{D}^{m} \times) α + C_{b}^{n} v_{D}^{m} δ K_{D}$

其中，

\phi_{D}

$ϕ_{D}$

是航位推算的姿态失准角，可以理解为姿态偏差角，这里的里程计是移动机器人中的车轮里程计，即车体

Y

$Y$

轴方向的速度

\mathcal{U}_{D}

$U_{D}$

，

(

)

C_{b}^{n}=C_{i j}(i, j=1,2,3)

$C_{b}^{n} = C_{ij} (i, j = 1, 2, 3)$

，将

[

]

v_{D}^{m}=\left[\begin{array}{lll} 0 & v_{D} & 0 \end{array}\right]^{\mathrm{T}}

$v_{D}^{m} = [0 v_{D} 0]^{T}$

带入上式得：

[

]

[

−

]

\tilde{v}_{D}^{n}=v_{D}^{n}+v_{D}^{n} \times \phi_{D}+\left[\begin{array}{ccc} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{array}\right]\left[\begin{array}{ccc} 0 & 0 & v_{D} \\ 0 & 0 & 0 \\ -v_{D} & 0 & 0 \end{array}\right] \alpha+

$\tilde{v}_{D}^{n} = v_{D}^{n} + v_{D}^{n} \times ϕ_{D} + ⎣ ⎡ C_{11} C_{21} C_{31} C_{12} C_{22} C_{32} C_{13} C_{23} C_{33} ⎦ ⎤ ⎣ ⎡ 00 - v_{D} 000 v_{D} 00 ⎦ ⎤ α +$

]

[

]

\left[\begin{array}{ccc} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{array}\right]\left[\begin{array}{c} 0 \\ v_{D} \\ 0 \end{array}\right] \delta K_{D}

$⎣ ⎡ C_{11} C_{21} C_{31} C_{12} C_{22} C_{32} C_{13} C_{23} C_{33} ⎦ ⎤ ⎣ ⎡ 0 v_{D} 0 ⎦ ⎤ δ K_{D}$

[

−

]

[

]

v_{D}^{n}+v_{D}^{n} \times \phi_{D}+v_{D}\left[\begin{array}{ccc} -C_{13} & 0 & C_{11} \\ -C_{23} & 0 & C_{21} \\ -C_{33} & 0 & C_{31} \end{array}\right] \alpha+v_{D}\left[\begin{array}{c} C_{12} \\ C_{22} \\ C_{32} \end{array}\right] \delta K_{D}

$v_{D}^{n} + v_{D}^{n} \times ϕ_{D} + v_{D} ⎣ ⎡ - C_{13} - C_{23} - C_{33} 000 C_{11} C_{21} C_{31} ⎦ ⎤ α + v_{D} ⎣ ⎡ C_{12} C_{22} C_{32} ⎦ ⎤ δ K_{D}$

从上式可以看出，滚动偏角

\alpha_{\gamma}

$α_{γ}$

不影响里程计的速度测量值。

1.4.2 轨迹相似性原理

假设在载车行驶过程中，一般水平姿态角都比较小（这个假设很重要），近似有：

≈

[

cos

⁡

−

sin

⁡

sin

⁡

cos

⁡

]

C_{b}^{n} \approx\left[\begin{array}{ccc} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{array}\right]

$C_{b}^{n} \approx ⎣ ⎡ cos ψ sin ψ 0 - sin ψ cos ψ 0 001 ⎦ ⎤$

容易得到如下公式，该公式在后面会用到：

(

)

≈

v_{D}^{n} \times u_{U}=\left(C_{b}^{n} v_{D}^{m}\right) \times u_{U} \approx

$v_{D}^{n} \times u_{U} = (C_{b}^{n} v_{D}^{m}) \times u_{U} \approx$

cos

⁡

−

sin

⁡

sin

⁡

cos

⁡

]

[

]

[

]

[

−

sin

⁡

cos

⁡

]

[

]

[

cos

⁡

sin

⁡

]

\left[\begin{array}{ccc} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} 0 \\ v_{D} \\ 0 \end{array}\right] \times\left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right]=v_{D}\left[\begin{array}{c} -\sin \psi \\ \cos \psi \\ 0 \end{array}\right] \times\left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right]=v_{D}\left[\begin{array}{c} \cos \psi \\ \sin \psi \\ 0 \end{array}\right]

$⎣ ⎡ cos ψ sin ψ 0 - sin ψ cos ψ 0 001 ⎦ ⎤ ⎣ ⎡ 0 v_{D} 0 ⎦ ⎤ \times ⎣ ⎡ 001 ⎦ ⎤ = v_{D} ⎣ ⎡ - sin ψ cos ψ 0 ⎦ ⎤ \times ⎣ ⎡ 001 ⎦ ⎤ = v_{D} ⎣ ⎡ cos ψ sin ψ 0 ⎦ ⎤$

上公式中

[

]

u_{U}=\left[\begin{array}{lll} 0 & 0 & 1 \end{array}\right]^{\mathrm{T}}

$u_{U} = [001]^{T}$

为天向单位矢量。

在姿态误差矢量

[

]

\phi_{D}=\left[\begin{array}{lll} \phi_{D E} & \phi_{D N} & \phi_{D U} \end{array}\right]^{\mathrm{T}}

$ϕ_{D} = [ϕ_{D E} ϕ_{D N} ϕ_{D U}]^{T}$

中，若忽略水平姿态误差影响，即近似

≈

\phi_{D E} \approx \phi_{D N} \approx 0

$ϕ_{D E} \approx ϕ_{D N} \approx 0$

，根据速度误差方程推导出来的

\tilde{v}_{D}^{n}

$\tilde{v}_{D}^{n}$

可得：

[

]

[

cos

⁡

sin

⁡

−

]

[

]

\tilde{v}_{D}^{n}=v_{D}^{n}+v_{D}^{n} \times\left[\begin{array}{c} 0 \\ 0 \\ \phi_{D U} \end{array}\right]+v_{D}\left[\begin{array}{ccc} 0 & 0 & \cos \psi \\ 0 & 0 & \sin \psi \\ -1 & 0 & 0 \end{array}\right]\left[\begin{array}{c} \alpha_{\theta} \\ \alpha_{\gamma} \\ \alpha_{\psi} \end{array}\right]+v_{D}^{n} \delta K_{D}=

$\tilde{v}_{D}^{n} = v_{D}^{n} + v_{D}^{n} \times ⎣ ⎡ 00 ϕ_{D U} ⎦ ⎤ + v_{D} ⎣ ⎡ 00 - 1 000 cos ψ sin ψ 0 ⎦ ⎤ ⎣ ⎡ α_{θ} α_{γ} α_{ψ} ⎦ ⎤ + v_{D}^{n} δ K_{D} =$

[

]

[

cos

⁡

sin

⁡

]

−

[

]

v_{D}^{n}+\phi_{D U} v_{D}^{n} \times\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right]+\alpha_{\psi} v_{D}\left[\begin{array}{c} \cos \psi \\ \sin \psi \\ 0 \end{array}\right]-\alpha_{\theta} v_{D}\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right]+v_{D}^{n} \delta K_{D}=

$v_{D}^{n} + ϕ_{D U} v_{D}^{n} \times ⎣ ⎡ 001 ⎦ ⎤ + α_{ψ} v_{D} ⎣ ⎡ cos ψ sin ψ 0 ⎦ ⎤ - α_{θ} v_{D} ⎣ ⎡ 001 ⎦ ⎤ + v_{D}^{n} δ K_{D} =$

−

v_{D}^{n}+\phi_{D U} v_{D}^{n} \times u_{U}+\alpha_{\psi} v_{D}^{n} \times u_{U}-\alpha_{\theta} v_{D} u_{U}+v_{D}^{n} \delta K_{D}=

$v_{D}^{n} + ϕ_{D U} v_{D}^{n} \times u_{U} + α_{ψ} v_{D}^{n} \times u_{U} - α_{θ} v_{D} u_{U} + v_{D}^{n} δ K_{D} =$

−

(

)

]

−

≈

\left[I-\left(\phi_{D U}+\alpha_{\psi}\right) u_{U} \times\right] v_{D}^{n}+\delta K_{D} v_{D}^{n}-\alpha_{\theta} v_{D} u_{U} \approx

$[I - (ϕ_{D U} + α_{ψ}) u_{U} \times] v_{D}^{n} + δ K_{D} v_{D}^{n} - α_{θ} v_{D} u_{U} \approx$

)

[

−

(

)

]

−

\left(1+\delta K_{D}\right)\left[I-\left(\phi_{D U}+\alpha_{\psi}\right) u_{U} \times\right] v_{D}^{n}-\alpha_{\theta} v_{D} u_{U}

$(1 + δ K_{D}) [I - (ϕ_{D U} + α_{ψ}) u_{U} \times] v_{D}^{n} - α_{θ} v_{D} u_{U}$

假设

\alpha_{\theta}, \phi_{D U}+\alpha_{\psi}, \delta K_{D}

$α_{θ}, ϕ_{D U} + α_{ψ}, δ K_{D}$

，且载车在地理位置变化不大的范围内行驶，即整个导航过程汇总导航坐标系的旋转变化不大，可近似当成平面看待，将上式积分可以得到位置方程，即为：

(

)

[

−

(

)

]

−

\tilde{S}_{D}^{n}=\left(1+\delta K_{D}\right)\left[I-\left(\phi_{D U}+\alpha_{\psi}\right) u_{U} \times\right] S_{D}^{n}-\alpha_{\theta} S_{D} u_{U}

$\tilde{S}_{D}^{n} = (1 + δ K_{D}) [I - (ϕ_{D U} + α_{ψ}) u_{U} \times] S_{D}^{n} - α_{θ} S_{D} u_{U}$

其中

∫

S_{D}^{n}=\int_{0}^{\mathrm{T}} v_{D}^{n} d t, \tilde{S}_{D}^{n}=\int_{0}^{\mathrm{T}} \tilde{v}_{D}^{n} d t, S_{D}=\int_{0}^{\mathrm{T}} v_{D} d t

$S_{D}^{n} = \int_{0}^{T} v_{D}^{n} d t, \tilde{S}_{D}^{n} = \int_{0}^{T} \tilde{v}_{D}^{n} d t, S_{D} = \int_{0}^{T} v_{D} d t$

，分别表示在时间段

]

[0, T]

$[0, T]$

内的载车真实位移矢量、计算位移矢量和行驶里程。

上公式可以分解为水平和垂直量部分，可得：

(

)

[

−

(

)

]

\tilde{S}_{D H}^{n}=\left(1+\delta K_{D}\right)\left[I-\left(\phi_{D U}+\alpha_{\psi}\right) u_{U} \times\right] S_{D H}^{n}

$\tilde{S}_{DH}^{n} = (1 + δ K_{D}) [I - (ϕ_{D U} + α_{ψ}) u_{U} \times] S_{DH}^{n}$

(

)

−

\tilde{S}_{D U}=\left(1+\delta K_{D}\right) S_{D U}-\alpha_{\theta} S_{D}

$\tilde{S}_{D U} = (1 + δ K_{D}) S_{D U} - α_{θ} S_{D}$

记

[

]

[

]

[

]

\tilde{S}_{D}^{n}=\left[\tilde{S}_{D E} \quad \tilde{S}_{D N} \quad \tilde{S}_{D U}\right]^{\mathrm{T}}, S_{D}^{n}=\left[S_{D E} \quad S_{D N} \quad S_{D U}\right]^{\mathrm{T}}, \tilde{S}_{D H}^{n}=\left[\tilde{S}_{D E} \quad \tilde{S}_{D N} \quad 0\right]^{\mathrm{T}}

$\tilde{S}_{D}^{n} = [\tilde{S}_{D E} \tilde{S}_{D N} \tilde{S}_{D U}]^{T}, S_{D}^{n} = [S_{D E} S_{D N} S_{D U}]^{T}, \tilde{S}_{DH}^{n} = [\tilde{S}_{D E} \tilde{S}_{D N} 0]^{T}$

，

[

]

S_{D H}^{n}=\left[\begin{array}{lll} S_{D E} & S_{D N} & 0 \end{array}\right]^{\mathrm{T}}

$S_{DH}^{n} = [S_{D E} S_{D N} 0]^{T}$

，右下标字符中的“H”表示在水平面的投影分量。

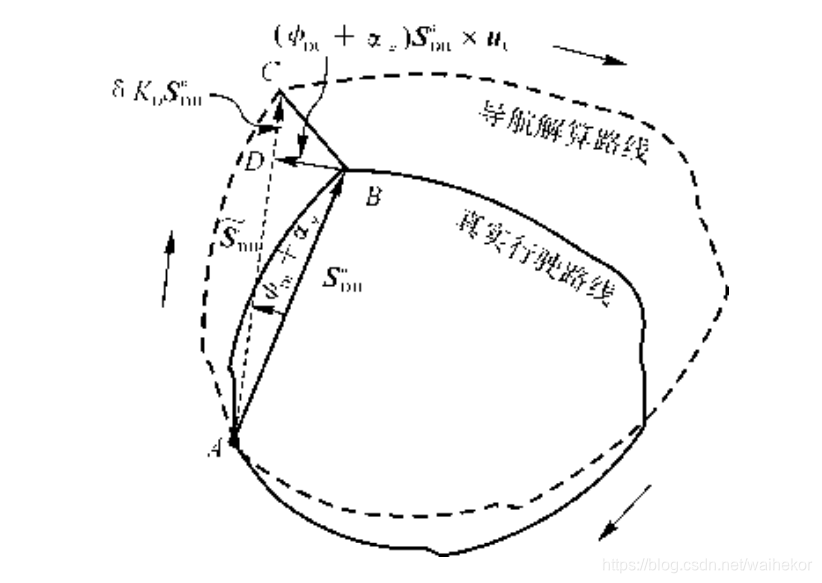
如下图所示，假设载车从A点沿某线路行驶一圈又回到A点。在行驶线路上任取一点B。图示

→

S_{D H}^{n}=\overrightarrow{A B}

$S_{DH}^{n} = A B$

为水平面上的真实位移，

→

\tilde{S}_{D H}^{n}=\overrightarrow{A C}

$\tilde{S}_{DH}^{n} = A C$

，为相应的计算位移，若做辅助线段BD使

⊥

B D \perp A C

$B D ⊥ A C$

，上面公式的几何含义是：真实位移

S_{D H}^{n}

$S_{DH}^{n}$

绕天向轴

u_{U}

$u_{U}$

转动角度

)

\left(\phi_{D U}+\alpha_{\psi}\right)

$(ϕ_{D U} + α_{ψ})$

得到

→

\overrightarrow{A D}

$A D$

，再扩大

)

\left(1+\delta K_{D}\right)

$(1 + δ K_{D})$

倍，得计算位移

\tilde{S}_{D H}^{n}

$\tilde{S}_{DH}^{n}$

，。由于在行驶路线上的每一点都满足以上几何规律，因此，导航解算路线和真实路线是几何相似的，即：以起始点A为中心点，解算路线在整体上转动了

)

\left(\phi_{D U}+\alpha_{\psi}\right)

$(ϕ_{D U} + α_{ψ})$

，角度并扩大了

)

\left(1+\delta K_{D}\right)

$(1 + δ K_{D})$

倍，这一特点称为航位推算轨迹与真实轨迹相似性原理。从图中还可以看出，

)

\left(\phi_{D U}+\alpha_{\psi}\right)

$(ϕ_{D U} + α_{ψ})$

将引起垂直于位移方向的误差

→

\overrightarrow{B D}

$B D$

，而

\delta K_{D}

$δ K_{D}$

会引起沿着位移方向的误差

→

\overrightarrow{D C}

$D C$

，这两项误差总和为

→

\overrightarrow{B C}

$BC$

，显然，载车行驶距起点越远误差越大，但是在返回起始点过程中，误差又会逐渐减少甚至消失。

航位推算的高度误差如下：

−

\delta S_{D U}=\tilde{S}_{D U}-S_{D U}=\delta K_{D} S_{D U}-\alpha_{\theta} S_{D}

$δ S_{D U} = \tilde{S}_{D U} - S_{D U} = δ K_{D} S_{D U} - α_{θ} S_{D}$

载车在行驶过程中，一般情况下行驶里程远大于其高度变化，即有

≫

S_{D} \gg S_{D U}

$S_{D} ≫ S_{D U}$

，当里程计刻度系数误差

\delta K_{D}

$δ K_{D}$

较小时，近似有：

≈

−

\delta S_{D U} \approx-\alpha_{\theta} S_{D}

$δ S_{D U} \approx - α_{θ} S_{D}$

这表明，航位推算的高度误差和俯仰安装误差角及行驶里程成正比，不论行驶路线如何，随着行驶里程增加，高度误差都会不断积累。

在这里插入图片描述

最后总结一下，如果不关注高度通道，组合导航轨迹和真实轨迹之间的偏航角是由于惯导器件偏航角误差和里程计和惯导之间的安装偏航角误差两方面引起的，由于这两个偏航角误差是耦合在一起的，所以标定出来的偏航角实际是两个误差累积结果，假定能通过其他观测数据相对精确辨识出其中一个，另外一个也就能解出来。

1.5 非线性优化方程建模与高斯牛顿算法

建模非线性优化函数的过程如下：

DVL自身测量坐标系为

m

$m$

，惯导坐标系为

b

$b$

，，DVL探底模式下得到的DVL速度分为

(

)

V_{D V L}^{m}=\left(\begin{array}{lll}\vartheta_{x}^{d v l} & \vartheta_{y}^{d v l} &\vartheta_{z}^{d v l} \end{array}\right)

$V_{D V L}^{m} = (ϑ_{x}^{d v l} ϑ_{y}^{d v l} ϑ_{z}^{d v l})$

，DVL速度的标度因数为

\delta k

$δ k$

，不考虑SINS和DVL之间的俯仰安装误差角，滚转安装误差角，只考虑SINS和DVL之间的方位安装误差角，设SINS和DVL之间的方位安装误差角为

\beta

$β$

，DVL数据更新时间为

\nabla t

$\nabla t$

，则航位推算公式如下：

]

[

]

⋅

[

(

)

(

)

(

)

]

⋅

∇

\left[\begin{array}{l} \Delta X_{D R}^{E} \\ \Delta X_{D R}^{N} \\ \Delta X_{D R}^{U} \end{array}\right]=\left[\begin{array}{c} \Delta X_{D R}^{E} \\ \Delta X_{D R}^{N} \\ \Delta X_{D R}^{U} \end{array}\right]+C_{b}^{n} C_{m}^{b} \cdot\left[\begin{array}{c} (1+\delta k) \vartheta_{x}^{A U V} \\ (1+\delta k) \vartheta_{y}^{A U V} \\ (1+\delta k) \vartheta_{Z}^{A U V} \end{array}\right] \cdot \nabla t

$⎣ ⎡ Δ X_{D R}^{E} Δ X_{D R}^{N} Δ X_{D R}^{U} ⎦ ⎤ = ⎣ ⎡ Δ X_{D R}^{E} Δ X_{D R}^{N} Δ X_{D R}^{U} ⎦ ⎤ + C_{b}^{n} C_{m}^{b} \cdot ⎣ ⎡ (1 + δ k) ϑ_{x}^{A U V} (1 + δ k) ϑ_{y}^{A U V} (1 + δ k) ϑ_{Z}^{A U V} ⎦ ⎤ \cdot \nabla t$

其中：

(

)

⋅

(

)

⋅

(

)

C_{b}^{n} C_{m}^{b}=\mathrm{R}\left(\mathrm{z}, \theta_{q}\right) \cdot \mathrm{R}\left(\mathrm{y}, \theta_{r}\right) \cdot \mathrm{R}\left(\mathrm{x}, \theta_{p}\right)

$C_{b}^{n} C_{m}^{b} = R (z, θ_{q}) \cdot R (y, θ_{r}) \cdot R (x, θ_{p})$

\theta_{q}=\theta_{y}+\beta

$θ_{q} = θ_{y} + β$

(

)

[

cos

⁡

(

)

−

sin

⁡

(

)

sin

⁡

(

)

cos

⁡

(

)

]

\mathrm{R}\left(\mathrm{z}, \theta_{q}\right)=\left[\begin{array}{ccc} \cos \left(\theta_{y}+\beta\right) & -\sin \left(\theta_{y}+\beta\right) & 0 \\ \sin \left(\theta_{y}+\beta\right) & \cos \left(\theta_{y}+\beta\right) & 0 \\ 0 & 0 & 1 \end{array}\right]

$R (z, θ_{q}) = ⎣ ⎡ cos (θ_{y} + β) sin (θ_{y} + β) 0 - sin (θ_{y} + β) cos (θ_{y} + β) 0 001 ⎦ ⎤$

(

)

[

cos

⁡

sin

⁡

−

sin

⁡

cos

⁡

]

\mathrm{R}\left(\mathrm{y}, \theta_{r}\right)=\left[\begin{array}{ccc} \cos \theta_{r} & 0 & \sin \theta_{r} \\ 0 & 1 & 0 \\ 0 & -\sin \theta_{r} & \cos \theta_{r} \end{array}\right]

$R (y, θ_{r}) = ⎣ ⎡ cos θ_{r} 00 01 - sin θ_{r} sin θ_{r} 0 cos θ_{r} ⎦ ⎤$

(

)

[

cos

⁡

−

sin

⁡

sin

⁡

cos

⁡

]

\mathrm{R}\left(\mathrm{x}, \theta_{p}\right)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ \cos \theta_{p} & -\sin \theta_{p} & 0 \\ 0 & \sin \theta_{p} & \cos \theta_{p} \end{array}\right]

$R (x, θ_{p}) = ⎣ ⎡ 1 cos θ_{p} 0 0 - sin θ_{p} sin θ_{p} 00 cos θ_{p} ⎦ ⎤$

GPS数据通过时间同步，时间同步包括硬件时间同步和软件时间同步，考虑到AUV本身的速度比较慢，软件时间同步采用线性插值的方法，得到每一个DVL数据所对应的GPS数据，并且保证在获取得到第一个DVL数据时，是有GPS数据的。

⋅

∇

\mathrm{T}=\mathrm{N} \cdot \nabla \mathrm{t}

$T = N \cdot \nabla t$

，时间

T

$T$

内，GPS经纬度转换到东北天坐标系下的位置表示如为：

]

⋯

\left[\begin{array}{c} X_{g p s, n}^{E} \\ X_{g p s, n}^{N} \end{array}\right], n=1,2,3 \cdots N

$[X_{g p s, n}^{E} X_{g p s, n}^{N}], n = 1, 2, 3 \dots N$

，GPS的位置增量计算公式如下：

]

[

]

−

[

]

⋯

\left[\begin{array}{c} \Delta X_{g p s, n}^{E} \\ \Delta X_{g p s, n}^{N} \end{array}\right]=\left[\begin{array}{c} X_{g p s, n}^{E} \\ X_{g p s, n}^{N} \end{array}\right]-\left[\begin{array}{c} X_{g p s, 0}^{E} \\ X_{g p s, 0}^{N} \end{array}\right], n=1,2,3 \cdots N

$[Δ X_{g p s, n}^{E} Δ X_{g p s, n}^{N}] = [X_{g p s, n}^{E} X_{g p s, n}^{N}] - [X_{g p s, 0}^{E} X_{g p s, 0}^{N}], n = 1, 2, 3 \dots N$

上公式中

]

\left[\begin{array}{c} X_{g p s, 0}^{E} \\ X_{g p s, 0}^{N} \end{array}\right]

$[X_{g p s, 0}^{E} X_{g p s, 0}^{N}]$

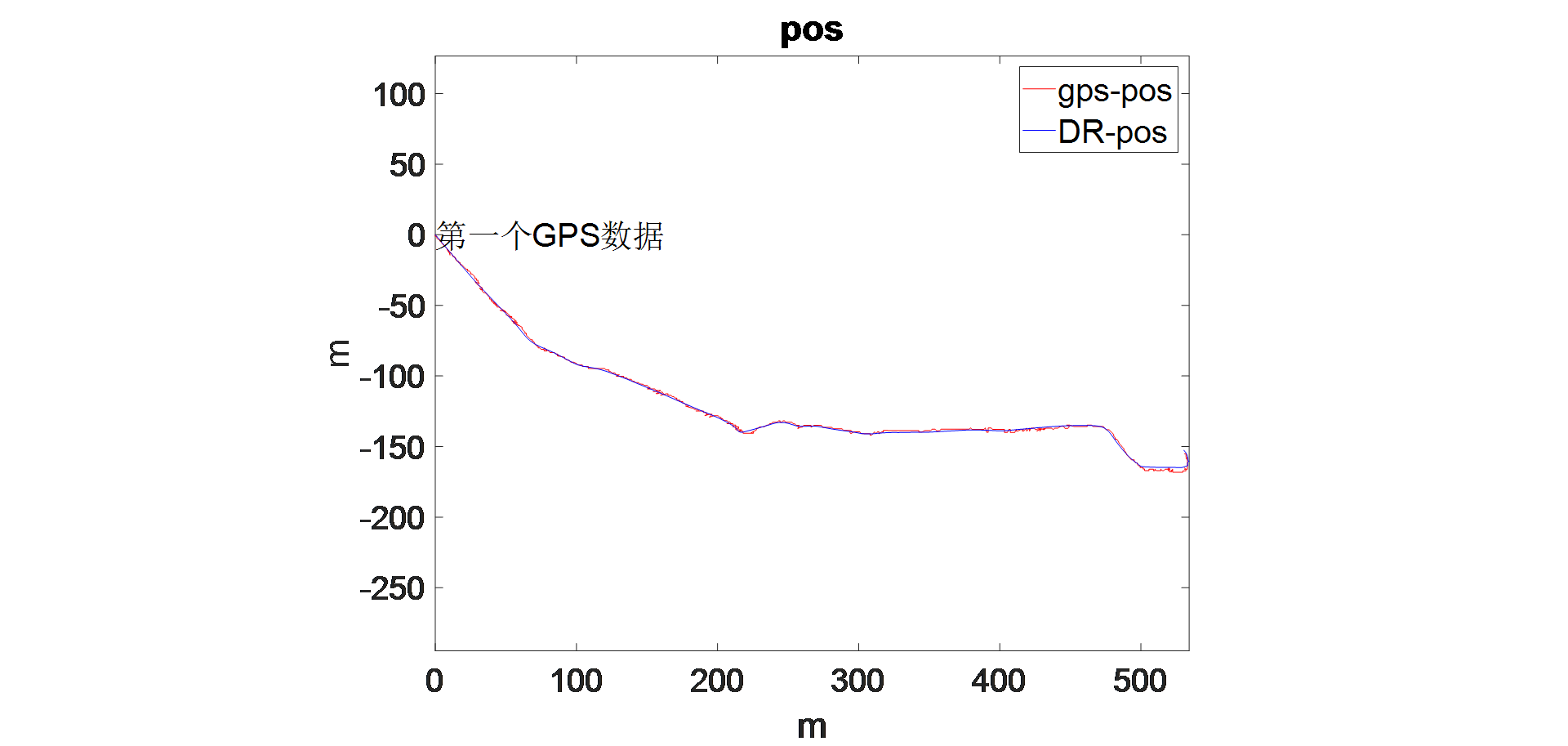
，为第一个GPS数据，航位推算位置数据和GPS数据均为增量数据，并且保证第一个DVL数据和GPS数据经过线性插值之后是对应的。

最终的优化函数描述如下：

⁡

[

]

∑

(

)

\operatorname{argmin}_{\left[\begin{array}{l} \beta \\ \delta k \end{array}\right]} \sum_{i=1}^{N}(f(\beta, \delta k))^{2}

$argmin_{[β δ k]} i = 1 \sum N (f (β, δ k))^{2}$

(

)

[

]

−

[

]

f(\beta, \delta k)=\left[\begin{array}{c} \Delta X_{g p s, i}^{E} \\ \Delta X_{g p s, i}^{N} \end{array}\right]-\left[\begin{array}{c} \Delta X_{D R, i}^{E} \\ \Delta X_{D R, i}^{N} \end{array}\right]

$f (β, δ k) = [Δ X_{g p s, i}^{E} Δ X_{g p s, i}^{N}] - [Δ X_{D R, i}^{E} Δ X_{D R, i}^{N}]$

要标定的参数是DVL速度的标度因数为

\delta k

$δ k$

，SINS和DVL之间的方位安装误差角为

\beta

$β$

，

(

)

f(\beta, \delta k)

$f (β, δ k)$

为关于

\beta, \delta k

$β, δ k$

的非线性函数。

下面我们用高斯牛顿方法求解上述非线性优化问题，过程如下：

另外

[

]

x=[\beta, \delta k]

$x = [β, δ k]$

，将

(

)

f(x)

$f (x)$

进行一阶泰勒展开

(

)

(

)

(

)

f(x+\Delta x)=f(x)+J(x) \Delta x

$f (x + Δ x) = f (x) + J (x) Δ x$

(

)

J(x)

$J (x)$

为

(

)

f(x)

$f (x)$

关于

x

$x$

的导数，也称为雅克比矩阵，当前的目标是寻找下降矢量

\Delta x

$Δ x$

，使得

(

)

∥

\|f(x+\Delta x)\|^{2}

$∥ f (x + Δ x) ∥^{2}$

达到最小，为了求

\Delta x

$Δ x$

，我们需要求解一个线性的最小二乘问题：

∗

argmin

⁡

∑

∥

(

)

(

)

∥

\Delta x^{*}=\operatorname{argmin}_{\Delta x} \sum_{i=1}^{N}\|f(x)+J(x) \Delta x\|^{2}

$Δ x^{*} = argmin_{Δ x} i = 1 \sum N ∥ f (x) + J (x) Δ x ∥^{2}$

可以看到经过上述转换，要优化的参数的由

x

$x$

变为

\Delta x

$Δ x$

，对目标函数的平方项进行展开：

∥

(

)

(

)

∥

∑

(

)

(

)

(

)

(

)

\sum_{i=1}^{N}\|f(x)+J(x) \Delta x\|^{2}=\sum_{i=1}^{N}(f(x)+J(x) \Delta x)^{T}(f(x)+J(x) \Delta x)

$i = 1 \sum N ∥ f (x) + J (x) Δ x ∥^{2} = i = 1 \sum N (f (x) + J (x) Δ x)^{T} (f (x) + J (x) Δ x)$

∑

∥

(

)

∥

(

)

(

)

(

)

(

)

=\sum_{i=1}^{N}\|f(x)\|^{2}+2 f(x)^{T} J(x) \Delta x+\Delta x^{T} J(x)^{T} J(x) \Delta x

$= i = 1 \sum N ∥ f (x) ∥^{2} + 2 f (x)^{T} J (x) Δ x + Δ x^{T} J (x)^{T} J (x) Δ x$

求上式关于

\Delta x

$Δ x$

的导数，并令其为0，得：

(

)

(

)

(

)

(

)

\sum_{i=1}^{N} 2 f(x)^{T} J(x)+2 J(x)^{T} J(x) \Delta x=0

$i = 1 \sum N 2 f (x)^{T} J (x) + 2 J (x)^{T} J (x) Δ x = 0$

得到如下方程组：

(

)

(

)

∑

−

(

)

(

)

\sum_{i=1}^{N}\left(J(x)^{T} J(x)\right) \Delta x=\sum_{i=1}^{N}-f(x)^{T} J(x)

$i = 1 \sum N (J (x)^{T} J (x)) Δ x = i = 1 \sum N - f (x)^{T} J (x)$

上述方程称为高斯牛顿方程或者增量方程，我们把左边的系数定义为

H

$H$

，右边定义为

g

$g$

，那么上式变为：

H \Delta x=g

$H Δ x = g$

高斯牛顿方法用

(

)

(

)

J(x)^{T} J(x)

$J (x)^{T} J (x)$

作为二阶海森矩阵的近似，求解增量方程是优化问题的核心所在。所以高斯牛顿算法的步骤如下：

1.给定初始值

x_{0}

$x_{0}$

2.对于第

k

$k$

次迭代，求出当前的雅克比矩阵

(

)

J\left(x_{k}\right)

$J (x_{k})$

和误差

(

)

f\left(x_{k}\right)

$f (x_{k})$

。

3.求解增量方程，

H \Delta x=g

$H Δ x = g$

。

4.若

x_{k}

$x_{k}$

，够小，或者迭代次数达到设定的最大值，则停止。否则，另

x_{k+1}=x_{k}+\Delta x_{k}

$x_{k + 1} = x_{k} + Δ x_{k}$

，返回2。

1.6 SINS/DR组合导航中的参数标定

以上场景下的SINS/DR组合导航，可以采用纯航位推算，并且标定安装误差和里程计刻度因子的方法。我使用的惯导是高精度光纤惯导，按照经验里程计和惯导之间的偏航安装角在1°以上，高精度光纤惯导的方位角误差和偏航安装角相比较小，可忽略，所以可以认为标定出来的偏航角误差即为它们之间的安装偏航角。因为不关注高度数据，所以需要标定的数据就只有两个，即里程计和SINS之间的安装偏航角和里程计的刻度因子。

参数标定过程类似加速度计误差的标定，常用非线性优化算法，例如高斯牛顿方法，LM算法等。优化函数采用平方根形式的导航定位精度，真值使用GPS数据，GPS的动态定位精度大约2m左右。

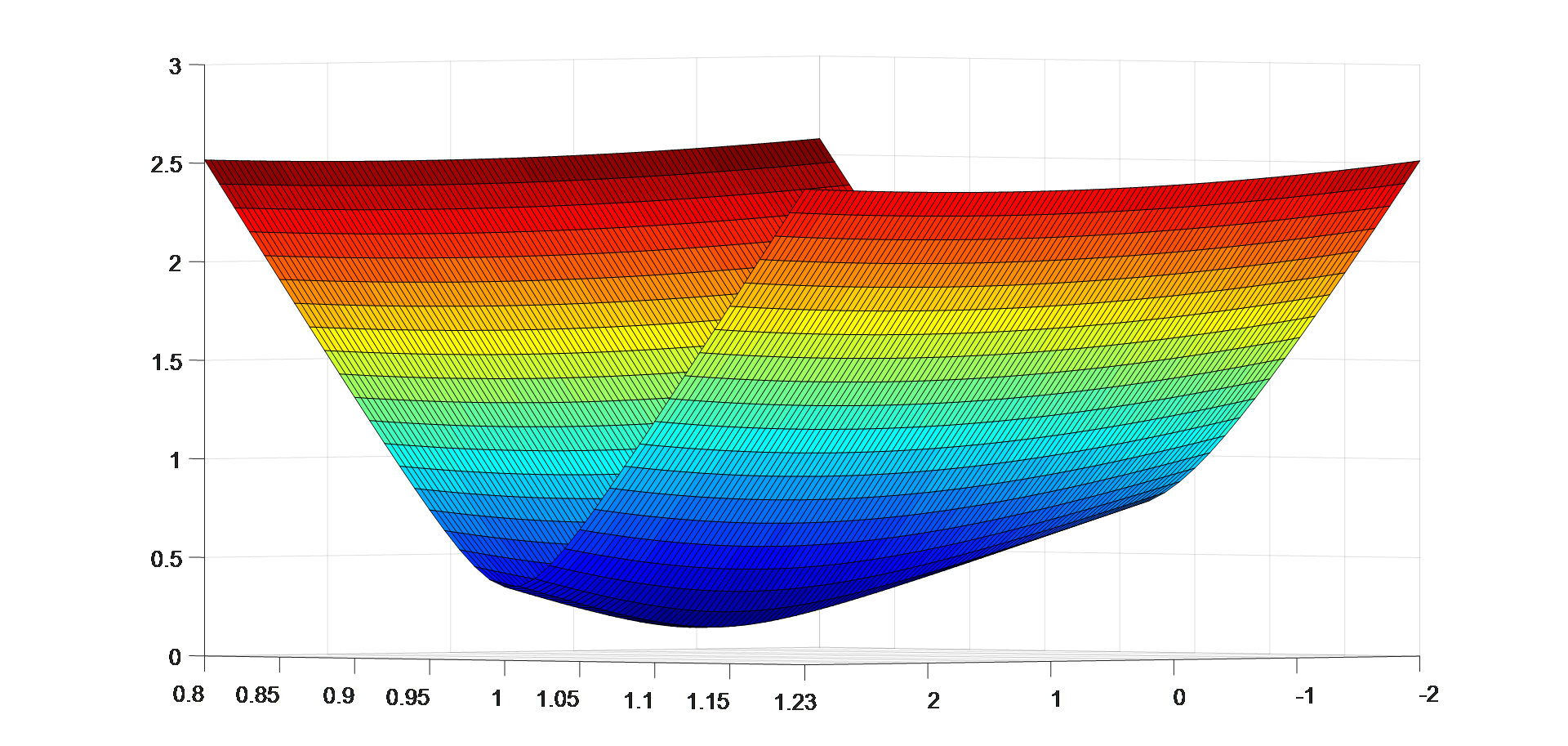
下图是DVL标度因子以及方位角安装误差两个待寻优参数的搜索空间，可以看到整个搜索空间没有出现“多峰”现象，对于高斯牛顿算法来说比较容易搜索到最优值。图中导航精度和两个待标定参数的变化规律，从图中可以看出只有一个极小值，极小值点的导航精度大约0.2%左右，由于不存在多个极值的情况，另外梯度方向比较清晰，所以对于标定来说是有利的。

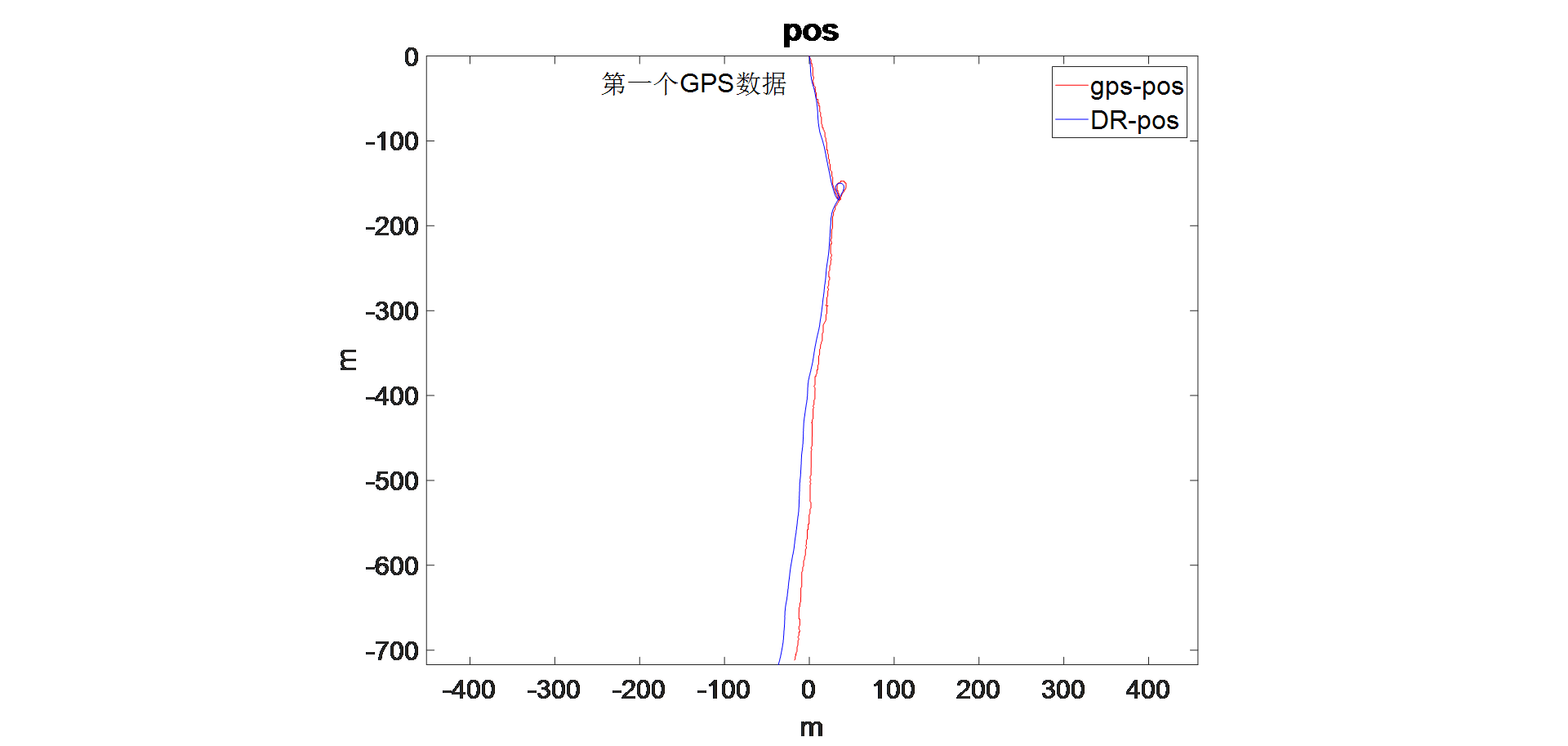
在这里插入图片描述

下图是没有标定误差的航位推算结果，计算出来的定位精度为2.31%，从图中可以看出很明显的两条轨迹之间的角度偏差。

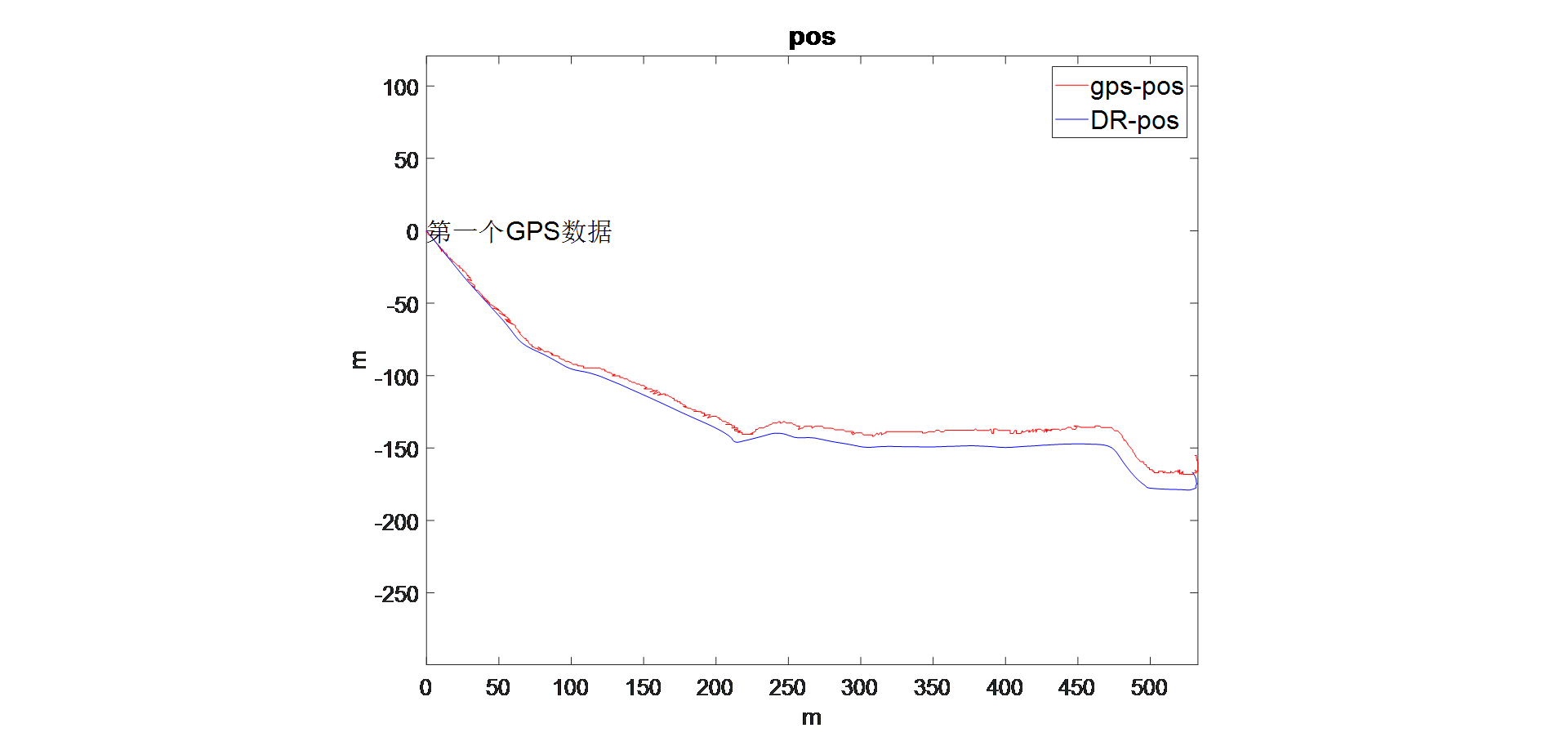
下图是通过非线性优化方法标定误差之后的航位推算结果，从图中可以看出很明显两条轨迹几乎重合，标定出来的误差如下：安装偏航角为1.44°，DVL刻度因子为0.995，从中也可以看出，两个误差中安装误差角所占比重较大。

在这里插入图片描述

然后按照这个已经标定好的两个误差参数，测试如下轨迹，没有经过误差标定的轨迹和经过误差标定的轨迹如下所示,其中经过误差标定的轨迹的定位精度为0.27%。

参考文献

车载自主定位定向系统研究（博士论文）严恭敏
捷联惯导算法与组合导航原理严恭敏等编著
A robust and easy to implement method for IMU calibration without external equipments
惯性导航精度评定方法 GJB 729-89

原文链接：https://blog.csdn.net/waihekor/article/details/105843608