? 前言
Wassup guys,我是Edison
?
今天是C语言每日一练,第117天!
Let’s get it!

1. 问题描述
中国古代数学家
张丘健
在他的
《算经》
中提出了一个著名的
“百钱百鸡问题”
?
一只公鸡值五钱,一只母鸡值三钱,三只小鸡值一钱,现在要用百钱买百鸡,请问公鸡、母鸡、小鸡各多少只?
2. 问题分析
如果用百钱
只买公鸡
,最多可以买20只,但题目要求买一百只,所以公鸡数量在
0~20
之间。同理,母鸡数量在
0~33
之间。在此把公鸡、母鸡和小鸡的数量分别设为
cock
、
hen
、
chicken
,则
co
c
k
+
h
e
n
+
c
h
i
c
k
e
n
=
100
cock+hen+chicken=100
c
o
c
k
+
h
e
n
+
c
h
i
c
k
e
n
=
1
0
0
因此百钱买百鸡问题就转换成解不定方程组的问题了:
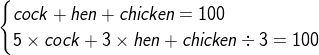
3. 算法思路
对于不定方程组,我们可以利用穷举循环的方法来解决。
公鸡范围是
0~20
,可用语句
for(cock=0; cock<=20; cock++)
实现。钱的数量是固定的,要买的鸡的数量也是固定的,母鸡数量是受到公鸡数量限制的。
同理,小鸡数量受到公鸡和母鸡数量的限制,因此可以利用三层循环的嵌套来解决:第一层循环控制公鸡数量,第二层控制母鸡数量,最里层控制小鸡数量。

4. 代码实现
?
#include <stdio.h>
int main()
{
int cock = 0;
int hen = 0;
int chicken = 0;
for (cock = 0; cock <= 20; cock++) //外层循环控制公鸡数量取值范围0~20
{
for (hen = 0; hen <= 33; hen++) //中层循环控制母鸡数量取值范围0~30
{
for (chicken = 0; chicken <= 100; chicken++) //内层循环控制小鸡数量取值范围0~100
{
//在内外层循环条件控制下小鸡数量的取值限制用难一组解的合理性
if ((5*cock + 3*hen + chicken/3.0 == 100) && (cock + hen + chicken == 100))
{
printf("cock=%2d, hen=%2d, chicken=%2d\n", cock, hen, chicken);
}
}
}
}
return 0;
}
运行结果?
5. 算法优化
以上算法需要穷举尝试
21∗
34
∗
101
=
72114
21 *34*101=72114
2
1
∗
3
4
∗
1
0
1
=
7
2
1
1
4
次,算法的效率明显太低了。对于本题来说,公鸡的数量确定后,小鸡的数量就是固定为
100−
c
o
c
k
−
h
e
n
100-cock-hen
1
0
0
−
c
o
c
k
−
h
e
n
,无须进行穷举了。此时约束条件就只有一个:
5∗
c
o
c
k
+
3
∗
h
e
n
+
c
h
i
c
k
e
n
/
3
=
100
5*cock+3*hen+chicken/3=100
5
∗
c
o
c
k
+
3
∗
h
e
n
+
c
h
i
c
k
e
n
/
3
=
1
0
0
。这样我们利用两重循环即可实现。
此算法只需尝试
21∗
34
=
714
21 * 34 = 714
2
1
∗
3
4
=
7
1
4
次,实现时约束条件中限定了
chicken
必须能被3整除。只有chicken能被3整除时才会继续进行约束条件
5∗
c
o
c
k
+
3
∗
h
e
n
+
c
h
i
c
k
e
n
/
3
=
100
5*cock+3*hen+chicken/3=100
5
∗
c
o
c
k
+
3
∗
h
e
n
+
c
h
i
c
k
e
n
/
3
=
1
0
0
的判断。这样省去了
chicken
不能被3整除时需要进行的算术计算和条件判断,进一步提高了算法的效率。

