参考文献下载地址：

Microphone_Array_Signal_Processing（中文版+英文版）

远场模型

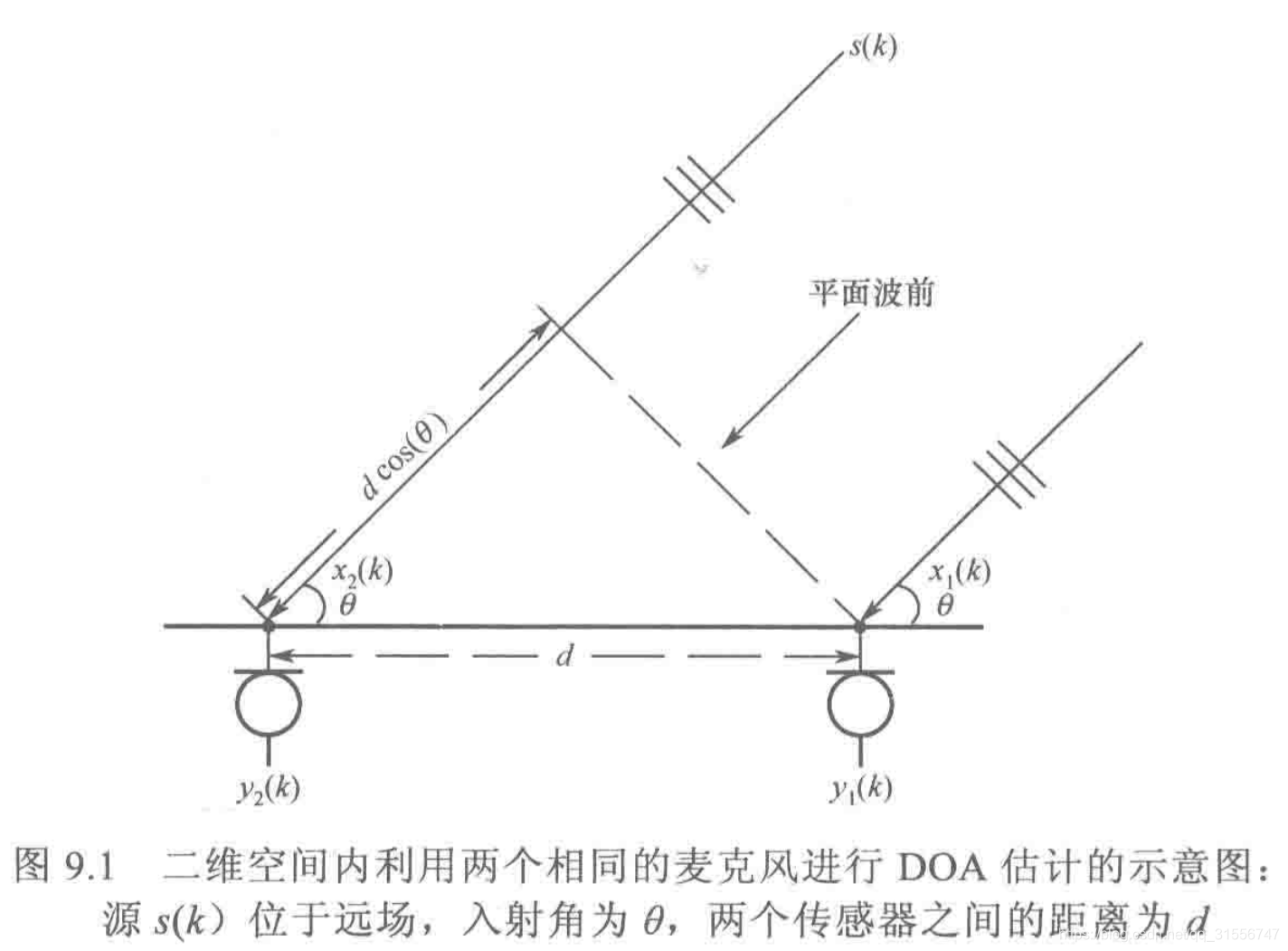
远场信号可以视为平面波，空气中声速为c，因此两个麦克风之间的相对时延为



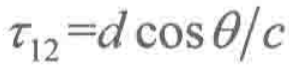
在麦克风阵列的物理结构确定的条件下（d已知），我们可以通过对时延进行估计，从而求解出声波的入射角度θ。

自由场信号模型

麦克风的接收信号可以被建模成



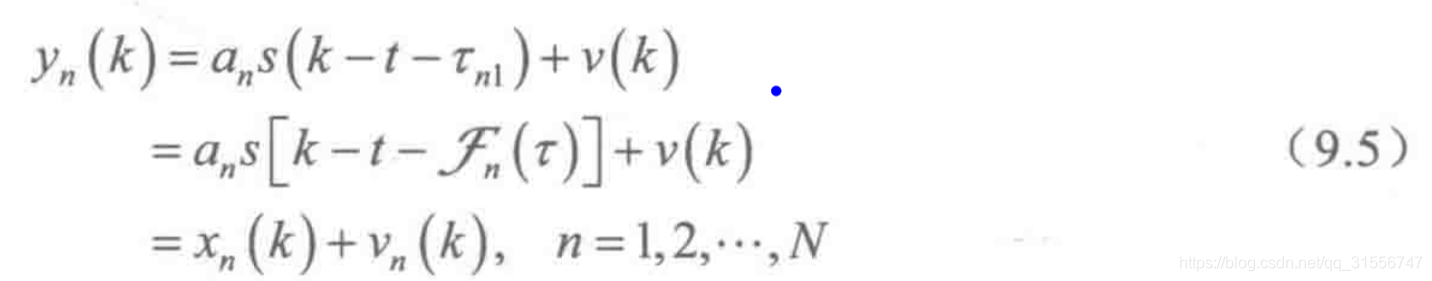
其中Vn(k)为加性噪声，Xn(k)为源信号与传递函数卷积的结果

互相关方法（Cross-Correlation,CC）

考虑两个麦克风，可以得到两个观测信号y1(k)和y2(k)，它们之间的互相关函数(

CCF

)为



将（9.5）带入（9.12），计算可得



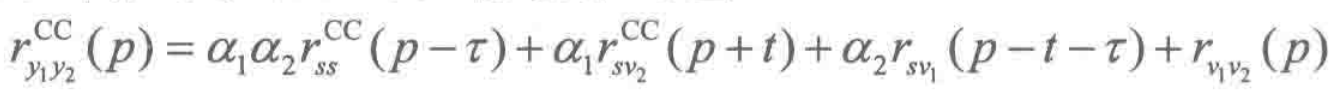
假设信号和噪声之间是不相关的，噪声和噪声之间也是不相关的，所以上式只有第一项不为零，且当p=τ时互相关函数达到最大。因此我们只需要求出互相关函数，计算峰值位置的偏移量，即为两个麦克风的相对时延。

广义互相关方法（Generalized Cross-correlation, GCC）

在麦克风阵列信号处理实际模型中，由于存在混响和噪声影响，导致CCF的峰值不明显，降低了时延估计的精度。为了锐化CCF的峰值，可以根据信号和噪声的先验知识，在频域内对互功率谱进行加权，从而能抑制噪声和混响干扰。最后进行傅里叶逆变换，得到广义互相关函数（

GCCF

）

广义互相关函数（

GCCF

）可以理解为滤波后的麦克风信号间的CCF，由于时域的互相关函数与频域的互功率谱是一对傅里叶变换对，因此GCCF可以写为



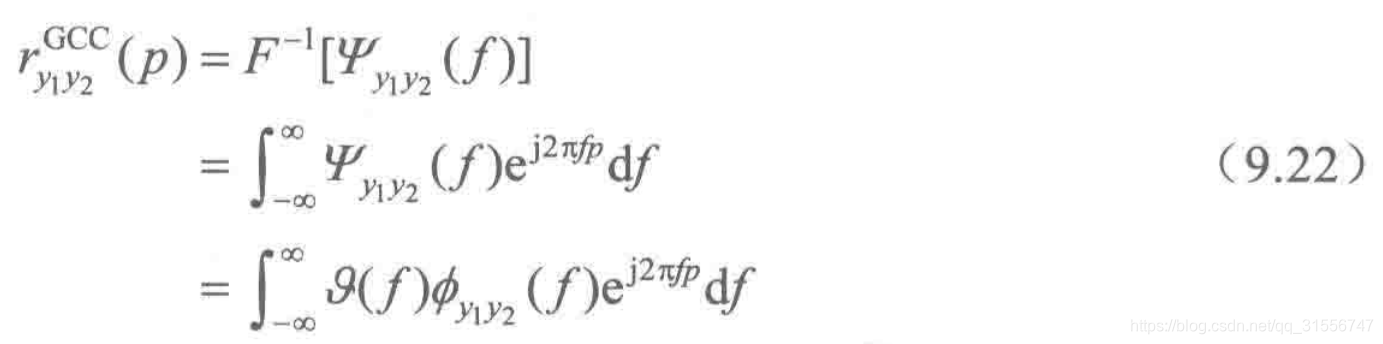
其中Φ可以看做互频谱，因此GCCF可以看做对互频谱进行频域加权后再进行逆FFT的结果


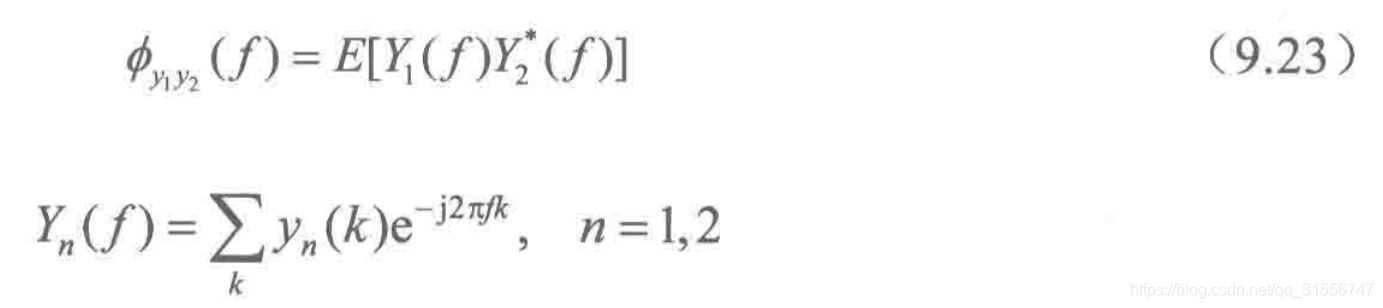
当频谱加权函数

θ

(f)=1时，GCC方法退化为CC方法。

GCC-PHAT方法

理想情况下，我们总是希望时域的互相关函数能够尽可能的尖锐，甚至趋近于δ函数；并且我们并不关心互相关函数每一点的幅值大小，我们只关心峰值出现的位置，换句话说我们更关心的是这个δ函数的时移。GCC-PHAT方法所采用的的频域加权函数（相位变换加权函数）如下


这样一来，互频谱的幅值部分被归一，广义频谱实则成为了互频谱的相位谱



将（9.32）带入（9.22），得到的GCC函数是一个δ函数的时移



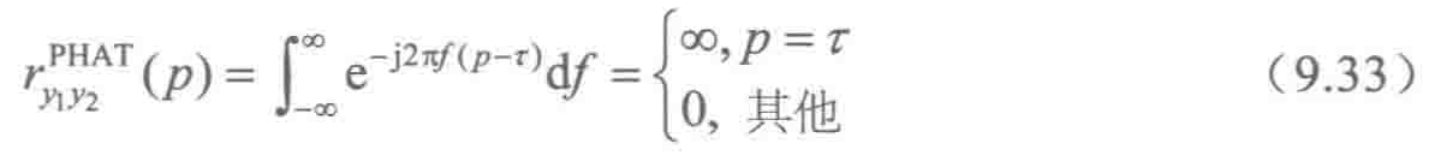
相位变换加权函数实质上是一个白化滤波器，它相当于将x1，x2两个信号白化成了存在一定时移的白噪声（等效于声源发出白噪声，经过一段距离的传播引入了时移，再被麦克风所接受），因此时域上的GCC变得更加尖锐了。

matlab实现

matlab中也提供了相应的函数包可以调用，tau = gccphat(sig,refsig,fs). 如果想了解代码细节可以参考我的程序，欢迎指正不足之处~代码下载地址：

GCC-PHAT算法demo


代码中定义正前方为0度，可以通过更改声源s，混响时间reverberation_time，声波入射角度sita等进行仿真实验。通过对比sita_re与sita的差距，可以分析算法在不同条件下的定位精度。

有如下的初步结论，欢迎讨论：

1. 阵列物理结构不变，混响强度不变，0度附近的声源定位精度更高；
2. 阵列物理结构不变，增大混响强度，定位精度变差，这是因为建模之初仅考虑了加性噪声，而混响与信号本身具有很强的相关性，建模时并未考虑这一点；
3. 混响强度不变，适当增大麦克风间距d，定位精度提高。如：将阵元间距增大至0.2m，500ms混响下依然可以准确定位。这是由于高频信号会发生混叠，阵元间隔增大，截止频率也随之升高，混叠减小。