参考:
https://blog.csdn.net/lemon_tree12138/article/details/50696926
RSA加密算法原理_张维鹏的博客-CSDN博客_rsa加密算法原理
图解RSA算法+取余和取模运算_养只猫叫泡芙的博客-CSDN博客_rsa算法中mod怎么算
RSA算法
RSA算法是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出,是最经典的
非对称加密算法
。非对称加密算法的特点就是加密秘钥和解密秘钥不同,秘钥分为公钥和私钥,用私钥加密的明文,只能用公钥解密;用公钥加密的明文,只能用私钥解密。它既能用于加密,也能用于数字签名,目前它已经成为最流行的公开密钥算法。SSH、OpenPGP、S/MIME、和SSL/TLS都依赖RSA的加密和签名功能。
一、RSA算法的数学基础
互质:
如果两个正整数,除了 1 以外没有其他公因子,就称这两个数是互质关系。比如 3 和 5,13 和 31 等。
欧拉函数:
求小于
N
的正整数中与
N
互质的数的数目。
例:对应 8,与 8 互质的数有 1,3,5,7,所以
φ
(
N
) = 4。
RSA 算法使用了欧拉函数的一个特例:如果 N可以分解成
两个互质的整数
之积:
N=pq ,则φ(N)=φ(p)φ(q)=(p−1)(q−1)。
例:φ(35947)=φ(103)φ(349)=(102)(348)=35496。
模反元素:
如果两个正整数 a和 n互质,那么一定可以找到整数 b,使得 ab−1被 n 整除: ab≡1 (mod
n
),这时,b就叫做 a的”模反元素”。
模反元素求解实例:
5*d=1 mod 52:(52*X+1)/5
5*d=1 mod 76:(76*X+1)/5 X从1 开始往上数->d
单向函数:
对于每一个输入,函数值都容易计算(多项式时间),但是给出一个随机输入的函数值,算出原始输入却比较困难(无法在多项式时间内使用确定性图灵机计算)。 单向函数是否存在仍然是计算机科学中的一个开放性问题。事实上,如果单向函数存在,将证明复杂性类P/NP问题中,P不等于NP。
在密码学中最常用的单向函数有两类,一是公开密钥密码中使用的单向陷门函数、二是消息摘要中使用的单向散列函数。
单向陷门函数:
首先是一个单向函数,在一个方向上易于计算而反方向却难于计算。但是,如果知道那个秘密陷门,则也能很容易在另一个方向计算这个函数。即已知x,易于计算y,而已知y,却难于计算x。然而,一旦给出y和一些秘密信息z,就很容易计算x。在公开密钥密码中,计算y相当于加密,陷门z相当于私有密钥,而利用陷门z求y中的x则相当于解密。
类似地,将许多大素数相乘要比将其乘积因式分解容易得多。数学上有很多函数看起来和感觉像
单向函数
,我们能够有效地计算它们,但我们至今未找到有效的求逆算法。我们把离散
对数函数
、RSA函数作为单向函数来使用,但是,目前还没有严格的数学证明表明所谓这些单向函数真正难以求逆,即单向函数是否存在还是未知的。
大数分解:
大
素数
分解,一般是指将一个合数(一般是两个大素数p,q的乘积pg)
因式分解
。在未知素数p,q很大的情况下,分解pq是非常有挑战性难度的。
二、RSA算法原理
RSA 算法的
可靠性
基础:
对极大整数做因数分解是很困难的,
对极大整数做因数分解的难度决定了RSA算法的可靠性。RSA算法的公钥和私钥是一对大素数(100到200位十进制数或更大)的相关函数,从一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积。
RSA 是非对称算法,加解密使用不同的密钥。
两个密钥都可以用于加密
,解密时需要使用另一个密钥。但是,因为公钥是近乎完全公开的,通常用公钥加密私钥解密。理论上 A 和 B 之间要通过 RSA 实现保密通信,需要 A 和 B 各自生成一组密钥,同时保管好自己的私钥;发送者用对方的公钥加密要发送的消息,接收者用自己的私钥解密对方发送过来的消息。在签名的场景下,用私钥签名,公钥验签。

RSA 比 DES 等对称算法慢得多。
一般在实际数据传输时,用 RSA 来加密比较短的对称密码,双方交换密码后再使用 DES 等对称算法加密数据。
RSA 加密或签名后的结果是
不可读的二进制
,使用时经常会转为 BASE64 码再传输。
RSA 加密时,对要加密数据的大小有限制,
最大不大于密钥长度
。例如在使用 1024 bit 的密钥时,最大可以加密 1024/8=
128 Bytes
的数据。数据大于 128 Bytes 时,需要
对数据进行分组加密
(如果数据超限,加解密时会失败,openssl函数会返回false),分组加密后的加密串拼接成一个字符串后发送给客户端。
为提高保密强度,RSA密钥至少为500位长,一般推荐用户(证书认证机构)使用1024位(2048位或以上)。这就使加密的计算量很大。为减少计算量,在传送信息时,常采用传统加密方法与公开密钥加密方法相结合的方式,即信息采用改进的AES或IDEA密钥加密,然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后,用不同的密钥解密并可核对信息摘要。
为了保证每次加密的结果都不同,RSA 加密时会在待加密数据后拼接一个随机字符串,再进行加密。不同的填充方式 Padding 表示这个字符串的不同长度,在对超限数据进行分组后,会按照这个 Padding 指定的长度填入随机字符串。例如如果 Padding 填充方式使用默认的 OPENSSL_PKCS1_PADDING(需要占用11个字节用于填充),那么
明文长度最多只能就是 128-11=117 Bytes
。
三、RSA算法流程

1、参数定义与密钥生成
注意:
-
模反元素存在,当且仅当
e
与 r 互质; - 将 p 和 q 的记录销毁;
- 公钥发送给所有的通信对象(对服务器来说就是所有的客户端),私钥则必须保管好,防止泄露;通过私钥可以轻松计算出公钥,反之不行。
2、加、解密、签名
加密:
假设客户端要向服务器发送消息 m,服务器的公钥是 n和 e。客户端将消息 m 转换为一个小于 N的非负整数 n,比如可以将每一个字转换为这个字的 Unicode 码,然后将这些数字连在一起组成一个数字。假如信息非常长的话,可以将这个信息分为几段,然后将每一段转换为 n。用下面这个公式他可以将 加密为 c:

计算 c并不复杂,客户端算出 c 后就可以将它传递给服务器。
解密:
得到消息 c后,可以利用密钥 d 来解码。可以用以下这个公式来将 c 转换为 n:

得到 n 后,可以将原来的信息 m 重新复原。解码的原理是:

已知 ed≡1(modr),即 ed=1+hφ(N)。由欧拉定理得:
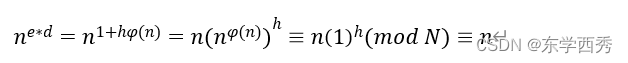
签名:
RSA 也可以用来为一个消息签名。签名应注意:不对数据M签名,而是对HASH(M)签名,可以使用时间戳,先签名后加密。实际应用中,对消息字符串的散列值(Message digest,用 MD5、SHA256 等算法求得的长度较短且固定的字符串)使用 RSA 的私钥进行签名(加密散列值)后,得到一个签名字符串,将其附加在消息字符串的合适位置后,一并发送。接收方使用对应的公钥可以从签名字符串中解密出原来的散列值,同时对原始消息再计算一次散列值。二者相比较,假如两者相符的话,则认为发信人持有正确的私钥,并且这个消息在传播路径上没有被篡改过。
待签名信息为x∈M,私有密钥d∈K,经过签名算法后得到y,且y∈A,即:

验证签名:
接收者接收到签名(y,x)后,应验证签名是否有效,即:

如果等式成立,则y是发送者对x 的有效签名,由于y是发送者使用其私钥经过算法所得,可有效防止发送者的抵赖行为。
四、RSA算法相关
密钥长度:
用户应使用 1024 位密钥,证书认证机构应用 2048 位或以上;
非对称:
用公钥加密时,私钥可以解密,反之亦然;核心运算是模幂运算,实现效率比较高效;
优势:
经受住了多年深入的密码分析,虽然密码分析者既不能证明也不能否定RSA的安全性,但这恰恰说明该算法有一定的可信性;
缺陷:
无法从理论上把握它的保密性能如何;产生密钥收到素数产生技术的限制;密钥分组产生高度较长,运算速度较低;
安全性:
在理论上,RSA的安全性取决于模n分解的困难性,但数学上至今还未证明分解模就是攻击RSA的最佳办法。
对RSA的攻击:
- 通过密文求明文;
- 通过暴力破解找出D;
- 通过E和N求D;
- 中间人攻击;
注意:保证RSA安全性就要保证选取的素数p和q足够大,
且为强素数,
e,d
不能太小,不能多个用户使用一个
n
。
五、RSA算法应用
- 苹果App签名
- HTTPS 加密连接
- 利用OpenSSL库对Socket传输进行安全加密
- SSH、OpenPGP、S/MIME、和SSL/TLS都依赖RSA的加密和签名功能
注:
如有错误、侵权,请联系笔者更改删除!!!