408计算机组成原理学习:数据的基础知识
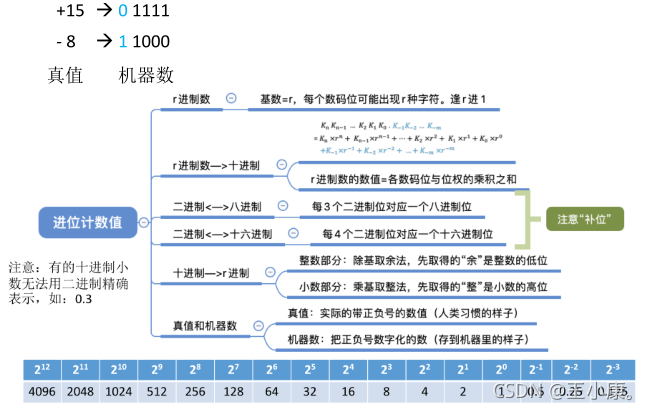
进位计数制
基数:每个数码位所用到的不同符号的个数,r 进制的基数为 r
二进制的好处:
①可使用两个稳定状态的物理器件表示
②0,1 正好对应逻辑值 假、真。方便实现逻辑运算
③可很方便地使用逻辑门电路实现算术运算
r进制转化为十进制
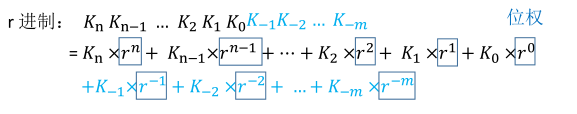
二进制与八进制和十六进制的转换
二进制 —> 八进制
3位一组,毎组转换成对应的八进制符号
Eg:

八进制—> 二进制
每位八进制对应的3位二进制
Eg:
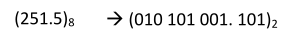
二进制 —> 十六进制
4位一组,毎组转换成对应的十六进制符号
Eg:
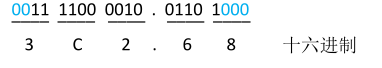
十六进制—> 二进制
每位十六进制对应的4位二进制
Eg:
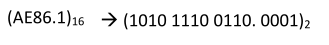
各种进制的常见书写方式:
二进制后面+B:1010001010010B
十进制后面 +D:1652D
十六进制后面 +H 或前面 +0x : 1652H或0x1652
十进制 —> 任意进制
对于一个r进制的数I
I = Kn Kn-1 Kn-2 … K2 K1 K0 K-1 K-2 … K-m
= Kn * r^n + Kn-1 * r^n-1 + … + K2 * r^2 + K1 * r^1 + K0 * r^0 + K-1*r^-1 + … + K-m * r^-m
转化为r进制步骤:
1.将整数部分 /r ,得到的余数为K0,再 /r,得到的余数为K1……
2.反复进行步骤1,直到除数为0,则将十进制的整数部分转化完毕
3.将十进值的小数*r,满1则记1,并将小数-1,不满1则记0
4.反复进行步骤3,直到十进制的小数部分为0
Eg:
75.3转化为二进制:
整数部分:

小数部分:
0.3D = 0.01001… B

注意:有的十进制小数无法用二进制精确表示,如:0.3
真值:符合人类习惯的数字
机器数:数字实际存到机器里的形式,正负号需要被“数字化”
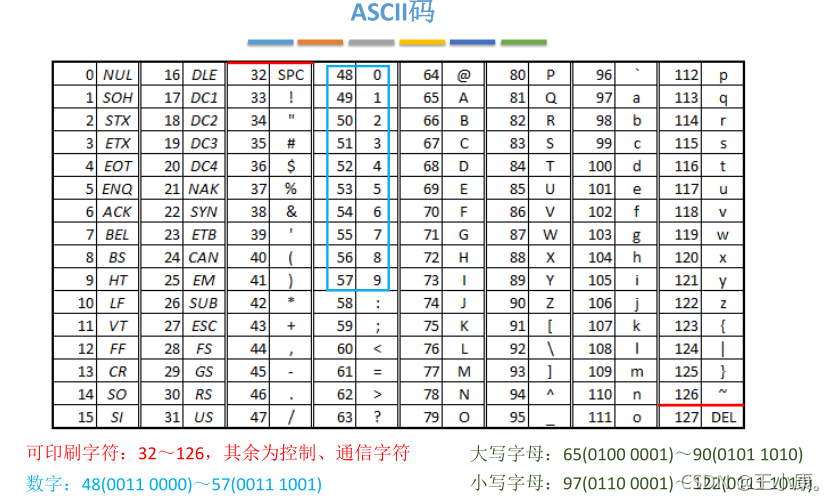
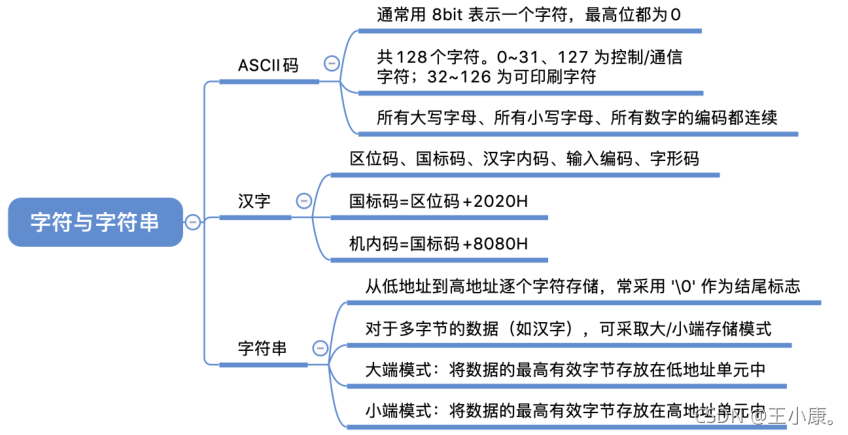
字符与字符串
数字
字母 三项共128个字符 —> 7位二进制编码 -> ASCII码
符号
ASCII码:为了存入计算机,通常在最高位补0,凑足1B
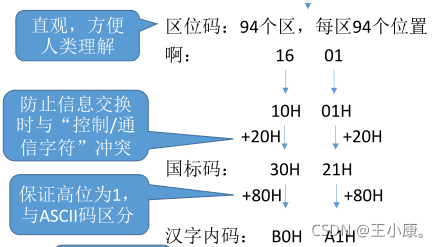
汉字的表示和编码
GB 2312-80 : 汉字+各种符号共7445个
区位码:94个区,每区94个位置
防止信息交换时与“控制/通信字符”冲突
保证高位为1,与ASCII码区分
输入:输入编码
输出:汉字字形码
字形码:

存储字符串时:
某计算机按字节编址即:每个地址对应1B
很多语言中,’ \0 ’作为字符串结尾标志
在所有计算机中,多字节数据都被存放在连续的字节序列中。根据数据中各字节的排列顺序不同,可能有“大端模式”、“小端模式”
大端模式:将数据的最高有效字节存放在低地址单元中
小端模式:将数据的最高有效字节存放在高地址单元中
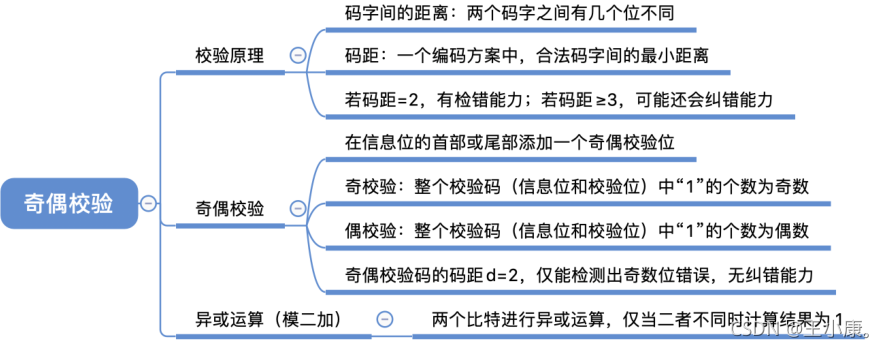
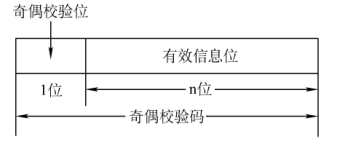
奇偶校验码
由若干位代码组成的一个字叫码字。
将两个码字逐位进行对比,具有不同的位的个数称为两个码字间的距离。
一种编码方案可能有若干个合法码字,各合法码字间的最小距离称为“码距”
即:A编码为00,C编码为10则俩个码字间的距离为1(不同的位数)
若:A编码为100,C编码为010则俩个码字间的距离为2
当码距d=1时,无检错能力;当d=2时,有检错能力;当d≥3时,若设计合理,可能具有检错、纠错能力
奇校验码 :整个校验码(有效信息位和校验位)中“1”的个数为奇数。
偶校验码 :整个校验码(有效信息位和校验位)中“1”的个数为偶数。
Eg:
给出编码1001101的奇偶校验码
有1001101中的‘1’的个数为偶数,故在首位添加一位1作为奇校验码
有1001101中的‘1’的个数为偶数,故在首位添加一位0作为偶校验码
奇偶校验码的局限性:如果编码发生多位错误则无法校验
偶校验的硬件实现:各信息进行异或(模2加)运算,得到的结果即为偶校验位
对编码进行偶校验(所有位(包括校验位)进行异或,若结果为1说明出错):