文章目录
前言
Apollo星火计划课程链接如下
星火计划2.0基础课:
https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课:
https://apollo.baidu.com/community/online-course/12
TASK系列解析文章
1.
【Apollo学习笔记】——规划模块TASK之LANE_CHANGE_DECIDER
2.
【Apollo学习笔记】——规划模块TASK之PATH_REUSE_DECIDER
3.
【Apollo学习笔记】——规划模块TASK之PATH_BORROW_DECIDER
4.
【Apollo学习笔记】——规划模块TASK之PATH_BOUNDS_DECIDER
5.
【Apollo学习笔记】——规划模块TASK之PIECEWISE_JERK_PATH_OPTIMIZER
6.
【Apollo学习笔记】——规划模块TASK之PATH_ASSESSMENT_DECIDER
7.
【Apollo学习笔记】——规划模块TASK之PATH_DECIDER
8.
【Apollo学习笔记】——规划模块TASK之RULE_BASED_STOP_DECIDER
9.
【Apollo学习笔记】——规划模块TASK之SPEED_BOUNDS_PRIORI_DECIDER&&SPEED_BOUNDS_FINAL_DECIDER
10.
【Apollo学习笔记】——规划模块TASK之SPEED_HEURISTIC_OPTIMIZER
11.
【Apollo学习笔记】——规划模块TASK之SPEED_DECIDER
12.
【Apollo学习笔记】——规划模块TASK之PIECEWISE_JERK_SPEED_OPTIMIZER
13.
【Apollo学习笔记】——规划模块TASK之PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER(一)
14.
【Apollo学习笔记】——规划模块TASK之PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER(二)
1. 速度规划算法总体介绍
Apollo中对路径规划解耦,分为路径规划与速度规划两部分。并将规划分为决策与优化两个部分。
•
路径规划
—— 静态环境(道路,静止/低速障碍物)
•
速度规划
—— 动态环境(中/高速障碍物)

## 1.1 速度规划的坐标系

速度规划的坐标系
注意:速度规划的
s
s
s
沿着轨迹的方向,路径规划的
s
s
s
沿着参考线的方向。
1.2 不同场景下的ST图
1.2.1 主车向前匀速行驶

1.2.2 主车先向前匀速行驶,后停车

1.2.3 主车跟随前车行驶

ps:蓝色四边形为障碍车在ST图下的投影。长边的斜率代表车速,短边代表障碍车在主车规划出的路径中占据的长度。
1.2.4 主车跟随前车刹停

1.2.5 障碍车在主车后方跟行

1.3 速度规划算法整体流程
路径规划的配置文件在
lane_follow_config.pb.txt
中
// /home/yuan/apollo-edu/modules/planning/conf/scenario/lane_follow_config.pb.txt
scenario_type: LANE_FOLLOW
stage_type: LANE_FOLLOW_DEFAULT_STAGE
stage_config: {
//路径规划
stage_type: LANE_FOLLOW_DEFAULT_STAGE
enabled: true
task_type: LANE_CHANGE_DECIDER
task_type: PATH_REUSE_DECIDER
task_type: PATH_LANE_BORROW_DECIDER
task_type: PATH_BOUNDS_DECIDER
task_type: PIECEWISE_JERK_PATH_OPTIMIZER
task_type: PATH_ASSESSMENT_DECIDER
task_type: PATH_DECIDER
task_type: RULE_BASED_STOP_DECIDER
//速度规划
task_type: SPEED_BOUNDS_PRIORI_DECIDER
task_type: SPEED_HEURISTIC_OPTIMIZER
task_type: SPEED_DECIDER
task_type: SPEED_BOUNDS_FINAL_DECIDER
task_type: PIECEWISE_JERK_SPEED_OPTIMIZER
# task_type: PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER
task_type: RSS_DECIDER
_DECIDER
结尾的为决策部分
_OPTIMIZER
结尾的为优化部分。
1.3.1 Task: SPEED_BOUNDS_PRIORI_DECIDER
产生速度可行驶边界

所形成的区域是非凸的,不能用之前凸优化的方法去做,需要用动态规划的方法去做。
1.3.2 Task:SPEED_HEURISTIC_OPTIMIZER
动态规划规划目标
- 加速度尽可能小
- 离障碍物纵向距离尽可能远
- 满足车辆加减速度要求
- 满足限速要求
产生粗糙速度规划曲线

1.3.3 Task: SPEED_DECIDER
产生速度决策

根据粗规划出的速度曲线,依据曲线在障碍物的上方还是下方,采取不同的决策。
1.3.4 Task: SPEED_BOUNDS_FINAL_DECIDER
产生速度规划边界


在障碍物的上方或下方确定可行使区域。
1.3.5 Task: PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER && PIECEWISE_JERK_SPEED_OPTIMIZER
产生平滑速度规划曲线


根据ST图的可行驶区域,优化出一条平滑的速度曲线。满足一阶导、二阶导平滑(速度加速度平滑);满足道路限速;满足车辆动力学约束。
PIECEWISE_JERK_SPEED_OPTIMIZER
基于二次规划的速度规划
PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER
基于非线性规划的速度规划
两者二选一即可
1.3.6 Stage: CombinePathAndSpeedProfile
将SL曲线、ST曲线合成为完整轨迹
,之后作为Planning的输出。

2. 基于动态规划的速度规划
2.1 动态规划
动态规划
——通过把原问题分解为相对简单的子问题,再根据子问题的解来求解出原问题解的方法

状态转移方程
f
(
P
)
=
min
{
f
(
R
)
+
w
R
→
P
}
f(P) = \min \{ f(R) + {w_{R \to P}}\}
f
(
P
)
=
min
{
f
(
R
)
+
w
R
→
P
}
2.2 基于动态规划的速度规划
基于动态规划的速度规划的流程如下:
1.对路程和时间进行采样
2.搜索出粗略的可行路线
3.选出代价最小的一条

2.2.1 对路程和时间进行采样

速度规划在ST图进行采样,在
t
t
t
的方向上以固定的间隔进行采样,在
s
s
s
方向上以先密后疏的方式进行采样(离主车越近,所需规划的精度就需更高;离主车越远,牺牲采样精度,提升采样效率)
// 时间采样的一般参数设置
unit_t: 1.0 //采样时间
dense_dimension_s: 101 // 采样密集区域的点数
dense_unit_s: 0.1 //采样密集区域的间隔
sparse_unit_s: 1.0 //采样系数区域的间隔
2.2.2 设计状态转移方程
2.2.2.1 障碍物cost计算

S_safe_overtake
超车的安全距离
S_safe_follow
跟车的安全距离
在设计状态转移方程时,要求不能与障碍物发生碰撞以及和障碍物不发生碰撞。于是可以得到以下方程:
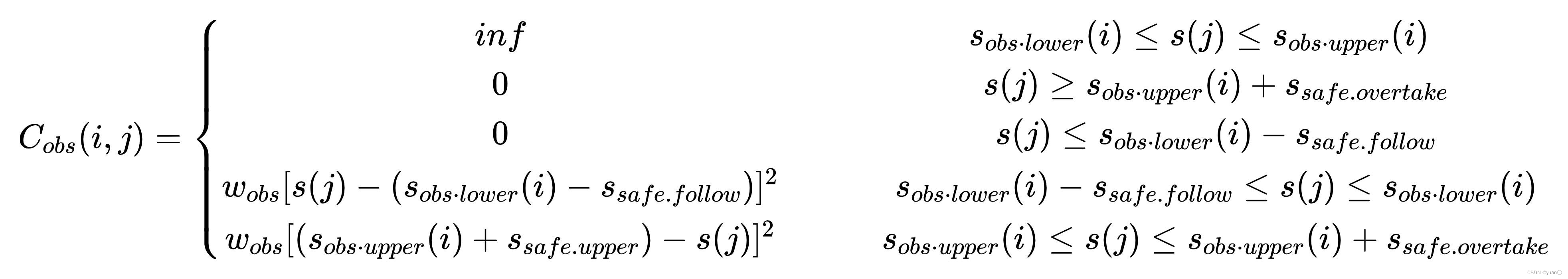
i
i
i
是
t
t
t
方向上的索引,
j
j
j
是
s
s
s
方向上的索引
如果在障碍物距离之内,则cost设为无穷;如果在安全距离之外,则cost设为0;如果在安全距离与障碍物之间,则按按之间的距离计算。
2.2.2.2 距离cost计算
目的是更快的到达目的地

距离cost计算方式如下
C
s
p
a
t
i
a
l
=
w
s
p
a
t
i
a
l
(
s
t
o
t
a
l
−
s
(
j
)
)
{C_{spatial}} = {w_{spatial}}({s_{total}} – s(j))
C
s
p
a
t
ia
l
=
w
s
p
a
t
ia
l
(
s
t
o
t
a
l
−
s
(
j
))
w
s
p
a
t
i
a
l
{w_{spatial}}
w
s
p
a
t
ia
l
为损失权值
(
s
t
o
t
a
l
−
s
(
j
)
)
({s_{total}} – s(j))
(
s
t
o
t
a
l
−
s
(
j
))
当前点到目标点的差值。
2.2.2.3 状态转移cost计算
状态转移cost计算分为三个部分:
C
e
d
g
e
=
C
s
p
e
e
d
+
C
a
c
c
+
C
j
e
r
k
{C_{edge}} = {C_{speed}} + {C_{acc}} + {C_{jerk}}
C
e
d
g
e
=
C
s
p
ee
d
+
C
a
cc
+
C
j
er
k
C
s
p
e
e
d
{C_{speed}}
C
s
p
ee
d
——速度代价
C
a
c
c
{C_{acc}}
C
a
cc
——加速度代价
C
j
e
r
k
{C_{jerk}}
C
j
er
k
——加加速度代价
节点间速度为:
v
=
s
(
j
+
k
)
−
s
(
j
)
Δ
t
v = \frac{
{s(j + k) – s(j)}}{
{\Delta t}}
v
=
Δ
t
s
(
j
+
k
)
−
s
(
j
)
限速比率:
v
det
=
v
−
v
l
i
m
i
t
v
l
i
m
i
t
{v_{\det }} = \frac{
{v – {v_{limit}}}}{
{
{v_{limit}}}}
v
d
e
t
=
v
l
imi
t
v
−
v
l
imi
t
C
s
p
e
e
d
{C_{speed}}
C
s
p
ee
d
速度代价的计算如下:

若速度<0,则是倒车的状况,轨迹不可行,代价值设为无穷大;若速度>0,且高于限速,则会有超速的惩罚;若速度<0,且低于限速,则会有低速的惩罚。在Apollo中,超速的惩罚值(1000)远大于低速的惩罚值(10)。

加速度的计算如下:
a
(
i
+
1
,
j
+
k
)
=
s
(
k
+
j
)
−
s
(
j
)
Δ
t
−
s
(
j
)
−
s
(
l
)
Δ
t
Δ
t
a(i + 1,j + k) = \frac{
{\frac{
{s(k + j) – s(j)}}{
{\Delta t}} – \frac{
{s(j) – s(l)}}{
{\Delta t}}}}{
{\Delta t}}
a
(
i
+
1
,
j
+
k
)
=
Δ
t
Δ
t
s
(
k
+
j
)
−
s
(
j
)
−
Δ
t
s
(
j
)
−
s
(
l
)
C
a
c
c
{C_{acc}}
C
a
cc
加速度代价的计算如下:

若超过最大加速度或小于最小加速度,则代价值设为无穷大,若在之间,Apollo设计了这样的代价函数进行计算:
y
=
x
2
+
x
2
1
+
e
x
+
4
+
x
2
1
+
e
x
+
2
y = {x^2} + \frac{
{
{x^2}}}{
{1 + {e^{x + 4}}}} + \frac{
{
{x^2}}}{
{1 + {e^{x + 2}}}}
y
=
x
2
+
1
+
e
x
+
4
x
2
+
1
+
e
x
+
2
x
2
其函数图像如下:

越靠近0,代价值越小;越靠近目标值,代价值越大,满足舒适性与平滑性。

加加速度的计算方式如下:
j
e
r
k
=
s
4
−
3
s
3
+
3
s
2
−
s
1
Δ
t
3
jerk = \frac{
{
{s_4} – 3{s_3} + 3{s_2} – {s_1}}}{
{\Delta {t^3}}}
j
er
k
=
Δ
t
3
s
4
−
3
s
3
+
3
s
2
−
s
1

加加速度超过设定边界,设为无穷;若在之间,则按二次方的方式进行计算。加加速度越小越好。
最后是总的代价:
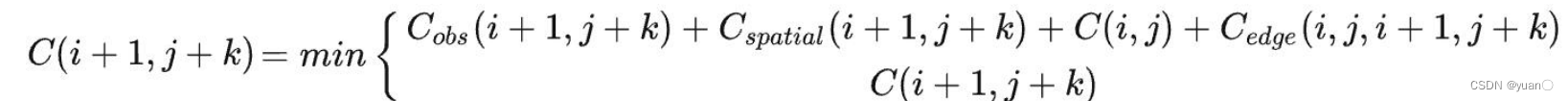
迭代范围:
![]()
在每次迭代时会将总的代价与当前节点的代价进行比较,取最小的一个,进行更新。

从
s
(
i
,
j
)
s(i,j)
s
(
i
,
j
)
到
s
(
i
+
1
,
j
+
k
)
s(i+1,j+k)
s
(
i
+
1
,
j
+
k
)
可以拓展到速度范围内的节点,按代价值的大小进行更新,最后按最后一列代价值最小的点进行求解,再进行回溯,得到ST曲线。
3. 基于二次规划的速度规划
动态规划得到的轨迹还比较粗糙,需要用优化的方法对轨迹进行进一步的平滑。基于二次规划的速度规划的方法与路径规划基本一致。
- 确定优化变量
- 设计目标函数
-
设计约束

3.1 确定优化变量

优化变量
x
x
x
,
x
x
x
有三个部分组成:从
s
0
s_0
s
0
,
s
1
s_1
s
1
,
s
2
s_2
s
2
到
s
n
−
1
s_{n-1}
s
n
−
1
,从
s
˙
0
\dot s_0
s
˙
0
,
s
˙
1
\dot s_1
s
˙
1
,
s
˙
2
\dot s_2
s
˙
2
到
s
˙
n
−
1
\dot s_{n-1}
s
˙
n
−
1
,从
s
¨
0
\ddot s_0
s
¨
0
,
s
¨
1
\ddot s_1
s
¨
1
,
s
¨
2
\ddot s_2
s
¨
2
到
s
¨
n
−
1
\ddot s_{n-1}
s
¨
n
−
1
.

ps:三阶导的求解方式为:
s
′
′
i
+
1
−
s
′
′
i
Δ
t
\frac{
{
{
{s”}_{i + 1}} – {
{s”}_i}}}{
{\Delta t}}
Δ
t
s
′′
i
+
1
−
s
′′
i
3.2 设计目标函数
对于目标函数的设计,我们需要明确以下目标:
-
尽可能贴合决策时制定的st曲线
:
∣s
i
−
s
i
−
r
e
f
∣
↓
\left| {
{s_i} – {s_{i – ref}}} \right| \downarrow
∣
s
i
−
s
i
−
re
f
∣
↓
-
确保舒适的体感,尽可能降低加速度/加加速度
:
∣s
¨
i
+
1
∣
↓
\left| {
{
{\ddot s}_{i + 1}}} \right| \downarrow
∣
s
¨
i
+
1
∣
↓
,
∣s
′
′
′
i
→
i
+
1
∣
↓
\left| {
{
{s”’}_{i \to i + 1}}} \right| \downarrow
∣
s
′′′
i
→
i
+
1
∣
↓
-
尽可能按照巡航速度行驶
:
∣s
˙
i
−
v
r
e
f
∣
↓
\left| {
{
{\dot s}_i} – {v_{ref}}} \right| \downarrow
∣
s
˙
i
−
v
re
f
∣
↓
-
在转弯时减速行驶, 曲率越大,速度越小
:
∣p
i
s
˙
i
∣
↓
\left| {
{p_i}{
{\dot s}_i}} \right| \downarrow
∣
p
i
s
˙
i
∣
↓
最后会得到以下目标函数:

w
s
w_s
w
s
——位置的权重
w
v
w_v
w
v
——速度的权重
p
i
p_i
p
i
——曲率的权重
w
a
w_a
w
a
——加速度的权重
w
j
w_j
w
j
——加加速度的权重
3.3 要满足的约束条件
接下来谈谈约束的设计。
要满足的约束条件
:
•
主车必须在道路边界内,同时不能和障碍物有碰撞
s
i
∈
(
s
min
i
,
s
max
i
)
{s_i} \in (s_{\min }^i,s_{\max }^i)
s
i
∈
(
s
m
i
n
i
,
s
m
a
x
i
)
•
根据当前状态,主车的横向速度/加速度/加加速度有特定运动学限制
:
![]()
•必须满足基本的物理原理:

•起始点约束:
;
s
0
=
s
i
n
i
t
s_0=s_{init}
s
0
=
s
ini
t
,
s
˙
0
=
s
i
n
i
t
\dot s_0=s_{init}
s
˙
0
=
s
ini
t
,
s
¨
0
=
s
i
n
i
t
\ddot s_0=s_{init}
s
¨
0
=
s
ini
t
满足的是起点的约束,即为实际车辆规划起点的状态。
3.4 转化为二次规划问题求解

代入OSQP求解器进行求解,输出一条平稳、舒适、能安全避开障碍物并且尽快到达目的地的速度分配曲线。
4. 基于非线性规划的速度规划
为了使得限速更加精细,Apollo提出了一种基于非线性规划的速度规划方法。
4.1 二次规划速度规划算法的问题


基于二次规划的速度规划中,
p
i
p_i
p
i
是曲率关于时间
t
t
t
的函数,但实际上路径的曲率是与
s
s
s
相关的。二次规划在原先动态规划出来的粗糙ST曲线上将关于
s
s
s
的曲率惩罚转化为关于
t
t
t
的曲率惩罚,如此,当二次规划曲线与动态规划曲线差别不大,规划出来基本一致;若规划差别大,则会差别很大。就如图所示,规划出来的区间差别较大。限速/曲率的函数是关于
s
s
s
的函数,而
s
s
s
是我们要求的优化量,只能通过动态规划进行转化,如此就会使得二次规划的速度约束不精确。
4.2 确定优化变量
基于非线性规划的速度规划步骤与之前规划步骤基本一致。

采样方式:等间隔的时间采样。
s
l
o
w
e
r
s_{lower}
s
l
o
w
er
与
s
u
p
p
e
r
s_{upper}
s
u
pp
er
为松弛变量,防止求解失败。
4.3 定义目标函数

目标函数与二次规划的目标函数差不多,增加了横向加速度的代价值以及松弛变量
w
s
o
f
t
s
l
o
w
e
r
w_{soft}s_{lower}
w
so
f
t
s
l
o
w
er
与
w
s
o
f
t
s
u
p
p
e
r
w_{soft}s_{upper}
w
so
f
t
s
u
pp
er
。
横向加速度的计算方式:
![]()
曲率是关于
s
s
s
的关系式,所以要进行平滑,对于非线性规划的求解器,无论是目标函数还是约束函数,都需要满足二阶可导:
κ
′
=
f
′
′
(
s
)
\kappa ‘ = f”(s)
κ
′
=
f
′′
(
s
)

曲率的平滑也是用到了二次规划的方法,用曲率的一阶导、二阶导、三阶导作为损失函数.

最后得到一条平滑曲率的曲线。
4.4 定义约束
接下来是约束条件:
-
规划的速度要一直往前走
:
si
≤
s
i
+
1
{s_i} \le {s_{i + 1}}
s
i
≤
s
i
+
1
-
加加速度不能超过定义的极限值
:
je
r
k
min
≤
s
¨
i
+
1
−
s
¨
i
Δ
t
≤
j
e
r
k
max
jer{k_{\min }} \le \frac{
{
{
{\ddot s}_{i{\rm{ + 1}}}} – {
{\ddot s}_i}}}{
{\Delta t}} \le jer{k_{\max }}
j
er
k
m
i
n
≤
Δ
t
s
¨
i
+
1
−
s
¨
i
≤
j
er
k
m
a
x
-
速度满足路径上的限速
:
s˙
i
≤
s
p
e
e
d
_
l
i
m
i
t
(
s
i
)
{\dot s_i} \le speed\_limit({s_i})
s
˙
i
≤
s
p
ee
d
_
l
imi
t
(
s
i
)
限速的函数并非直接可以得到,接下来看看限速函数是怎么来的。
限速的来源如下图所示:

将所有的限速函数相加,得到下图的限速函数,很明显,该函数既不连续也不可导,所以需要对其进行平滑处理。

对于限速曲线的平滑,Apollo采样分段多项式进行平滑,之后采样二次规划的方式进行求解。限速曲线的目标函数如下:

如此,我们就有了连续且可导的限速曲线。
再回到约束中,为了避免求解的失败,二次规划中对位置的硬约束,在非线性规划中转为了对位置的软约束。提升求解的精度。

同时还需满足基本的物理学原理

4.5 求解器求解
最后代入Ipopt中进行非线性规划的求解。
Ipopt(Interior Point Optimizer)是一个用于大规模非线性优化的开源软件包。它可用于解决如下形式的非线性规划问题:

g
L
{g^L}
g
L
和
g
U
{g^U}
g
U
是约束函数的上界和下界,
x
L
{x^L}
x
L
和
x
U
{x^U}
x
U
是优化变量的上界和下界。
Ipopt的求解由以下几个函数构成:
1.
get_nlp_info()
定义问题规模
/** Method to return some info about the nlp */
bool get_nlp_info(int &n, int &m, int &nnz_jac_g, int &nnz_h_lag,
IndexStyleEnum &index_style) override;
• 优化变量数量:
n
• 约束函数数量:
m
• 雅可比矩阵非0项数量:
nnz_jac_g
• 黑塞矩阵非0项数量:
nnz_h_lag
2.
get_bounds_info()
定义约束边界约束
/** Method to return the bounds for my problem */
bool get_bounds_info(int n, double *x_l, double *x_u, int m, double *g_l,
double *g_u) override;
• 自变量的下边界:
x_l
• 自变量的上边界:
x_u
• 约束函数下边界:
g_l
• 约束函数的上边界:
g_u
3.
get_starting_point()
定义初值
/** Method to return the starting point for the algorithm */
bool get_starting_point(int n, bool init_x, double *x, bool init_z,
double *z_L, double *z_U, int m, bool init_lambda,
double *lambda) override;
• 定义优化变量的初始值
x
对于速度规划问题,如何计算初始解?
Apollo同样用分段多项式二次规划的求解方式,得到符号约束的速度平滑曲线,作为非线性规划的初值。

4.
eval_f()
求解目标函数
/** Method to return the objective value */
bool eval_f(int n, const double *x, bool new_x, double &obj_value) override;
• 变量值:
x
• 目标函数值:
obj_val
5.
eval_grad_f()
求解梯度
/** Method to return the gradient of the objective */
bool eval_grad_f(int n, const double *x, bool new_x, double *grad_f) override;
• 变量值:
x
• 梯度值:
grad_f
梯度的定义:

目标函数:

![]()
偏导数:




6.
eval_g()
求解约束函数
/** Method to return the constraint residuals */
bool eval_g(int n, const double *x, bool new_x, int m, double *g) override;
• 变量值:
x
• 约束函数值:
g
7.
eval_jac_g()
求解约束雅可比矩阵
/** Method to return:
* 1) The structure of the jacobian (if "values" is nullptr)
* 2) The values of the jacobian (if "values" is not nullptr)
*/
bool eval_jac_g(int n, const double *x, bool new_x, int m, int nele_jac,
int *iRow, int *jCol, double *values) override;
• 变量值:
x
• 雅可比矩阵非0元素数量:
nele_jac
• 雅可比矩阵值:
values
雅可比矩阵:

求解器通过稀疏矩阵来保存值。


稀疏矩阵的例子
求解雅可比矩阵需要对约束函数进行求偏导:

微分关系等式约束:




8.
eval_h()
求解黑塞矩阵
/** Method to return:
* 1) The structure of the hessian of the lagrangian (if "values" is
* nullptr) 2) The values of the hessian of the lagrangian (if "values" is not
* nullptr)
*/
bool eval_h(int n, const double *x, bool new_x, double obj_factor, int m,
const double *lambda, bool new_lambda, int nele_hess, int *iRow,
int *jCol, double *values) override;
• 变量值:·x·
• 拉格朗日乘数:·lambda·
• 黑塞矩阵值:·values·
• 目标函数因数:·obj_factor·
黑塞矩阵:
![]()

拉格朗日函数

Ipopt的拉格朗日黑塞矩阵:

目标函数的二阶偏导数:

约束函数的二阶偏导数:

9.
finalize_solution()
/** @name Solution Methods */
/** This method is called when the algorithm is complete so the TNLP can
* store/write the solution */
void finalize_solution(Ipopt::SolverReturn status, int n, const double *x,
const double *z_L, const double *z_U, int m,
const double *g, const double *lambda,
double obj_value, const Ipopt::IpoptData *ip_data,
Ipopt::IpoptCalculatedQuantities *ip_cq) override;
目标函数取得最小值时的优化量:
x
目标函数最小值:
obj_value
5. 速度规划算法实践
云实验地址——
Apollo规划之速度规划仿真调试
1.启动DreamView
bash scripts/bootstrap.sh
模式选择Mkz Standard Debug,地图选择Apollo Virutal Map,打开Sim Control模式,打开PNC Monitor,等待屏幕中间区域出现Mkz车模型和地图后即表示成功进入仿真模式。
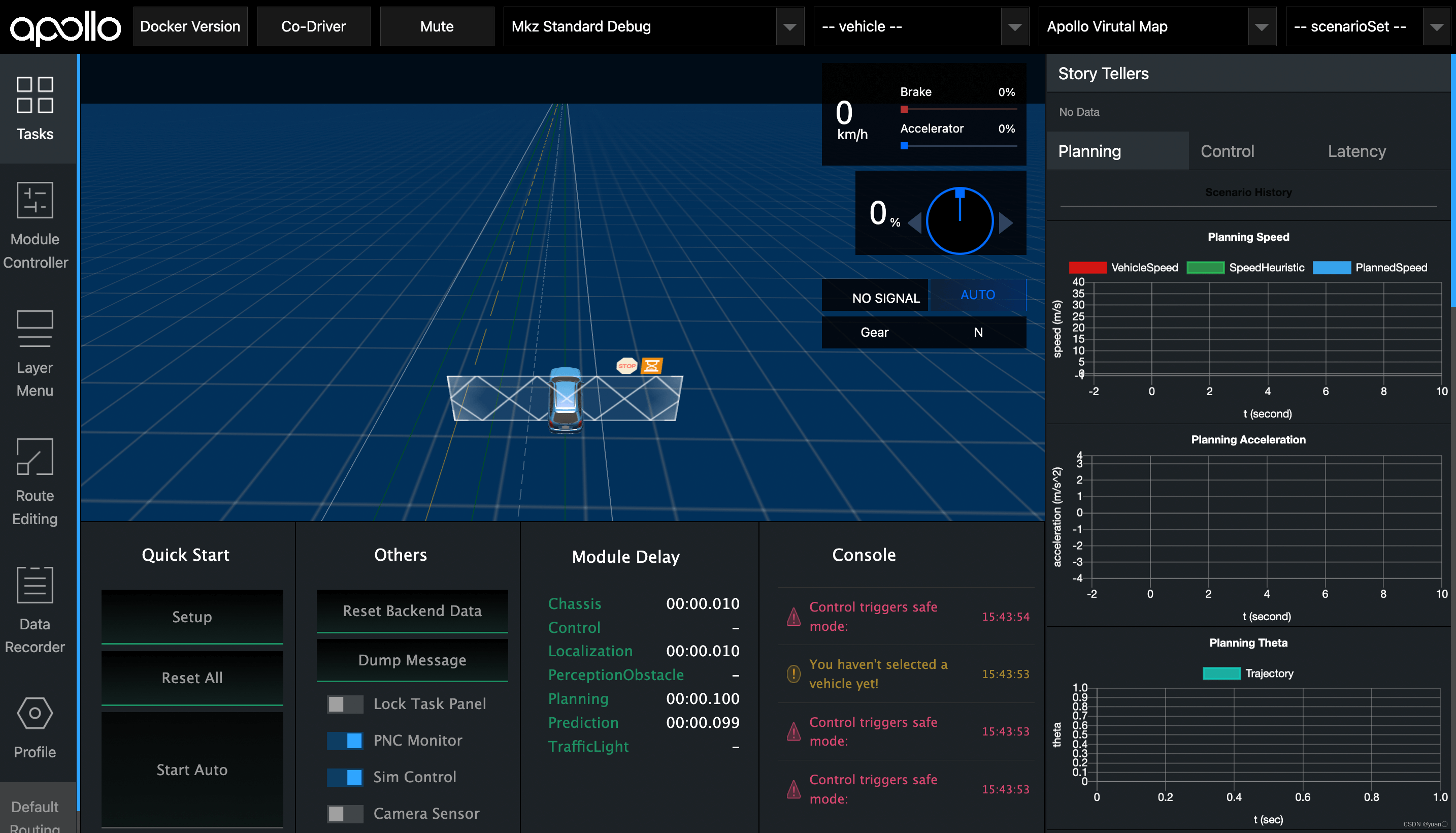
点击左侧Tab栏Module Controller,启动Planning,Prediction, Routing模块, 如果需要录制数据则打开Recorder模块。
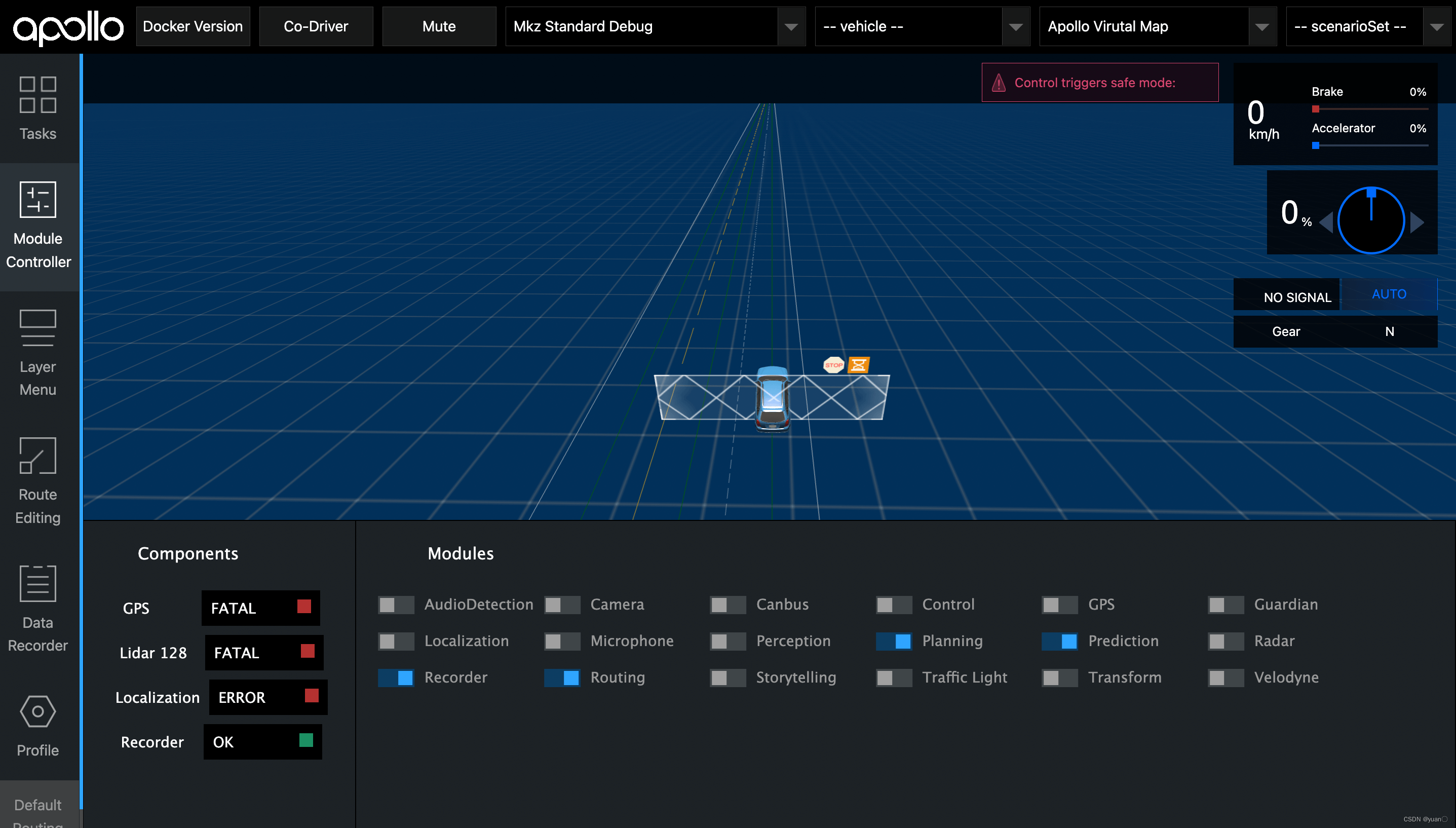
模块启动完成后,点击左侧Tab栏Profile, 选择Scenario Profiles里的course场景集,右上角选择场景场景开始仿真,点击减速让行场景和加速超车场景,观察PNC Monitor st曲线区别.
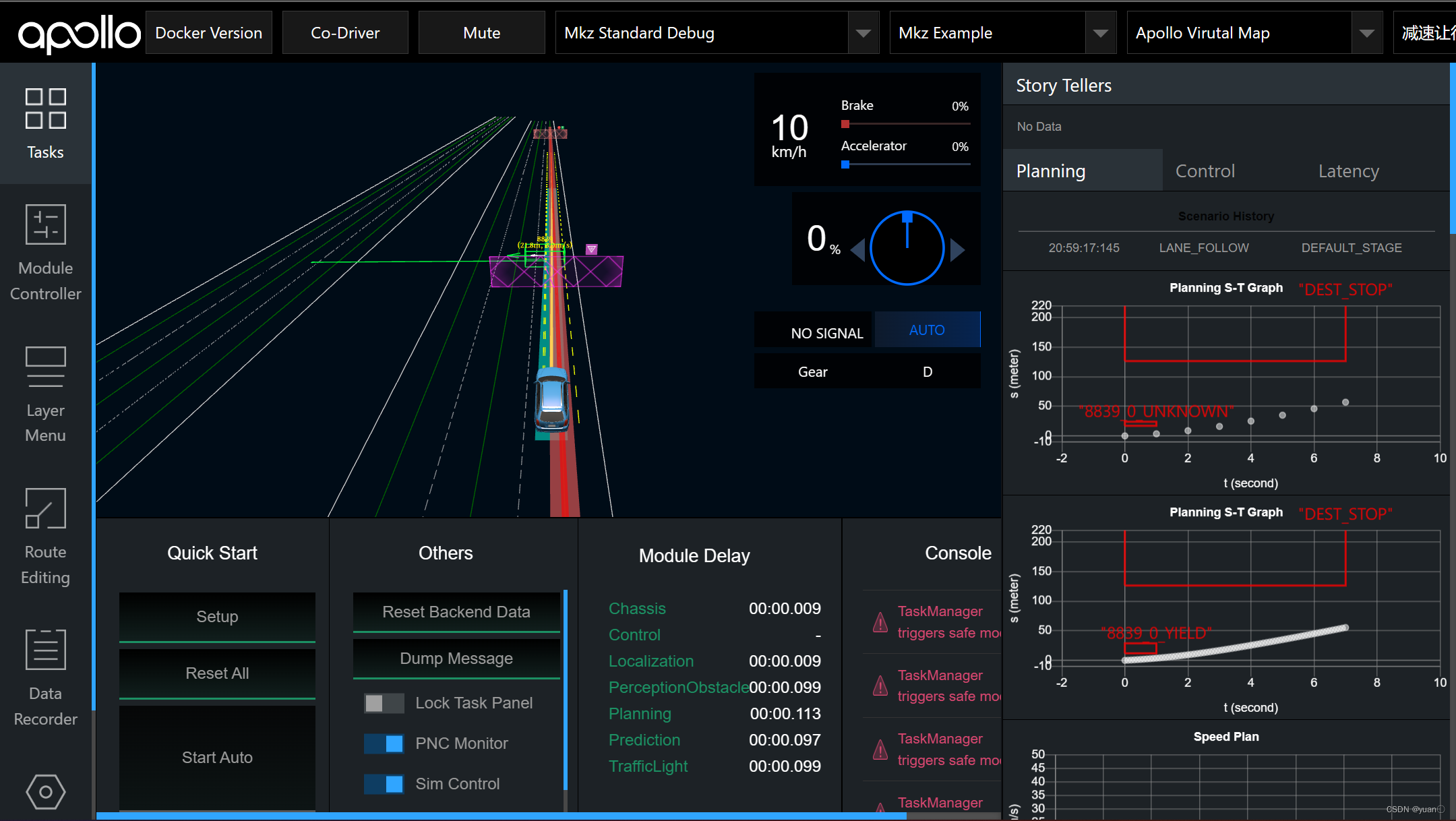
PNC Monitor中上方的st图是动态规划生成的st曲线,下方的st图是优化算法生成的st曲线

5.1 加速超车,减速让行场景速度规划实践
减速让行的场景,可以看到规划出的曲线在ST图中位于障碍物的下方。
加速超车的场景,可以看到规划出的曲线在ST图中位于障碍物的上方。
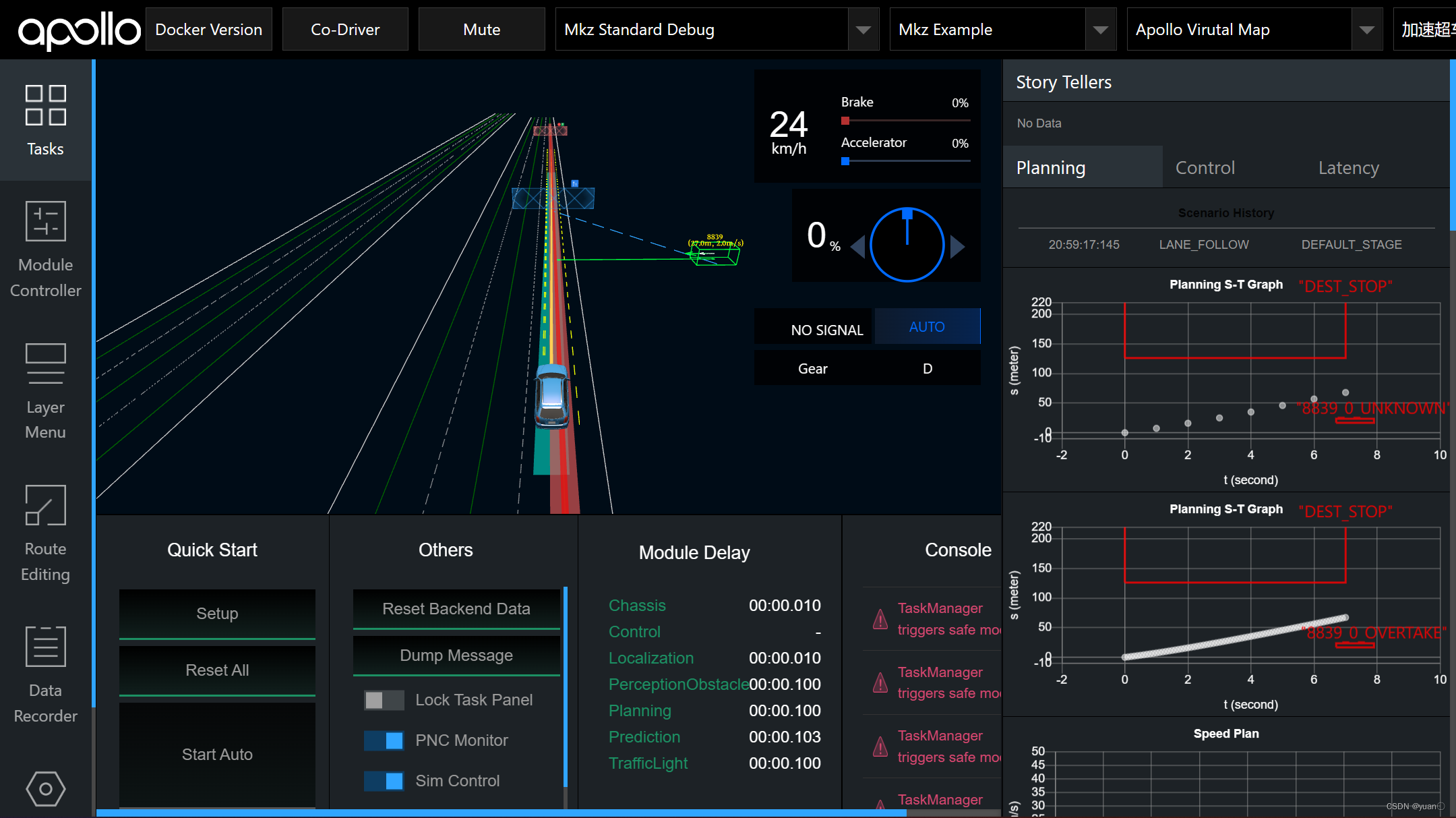
5.2 弯道场景速度规划实践
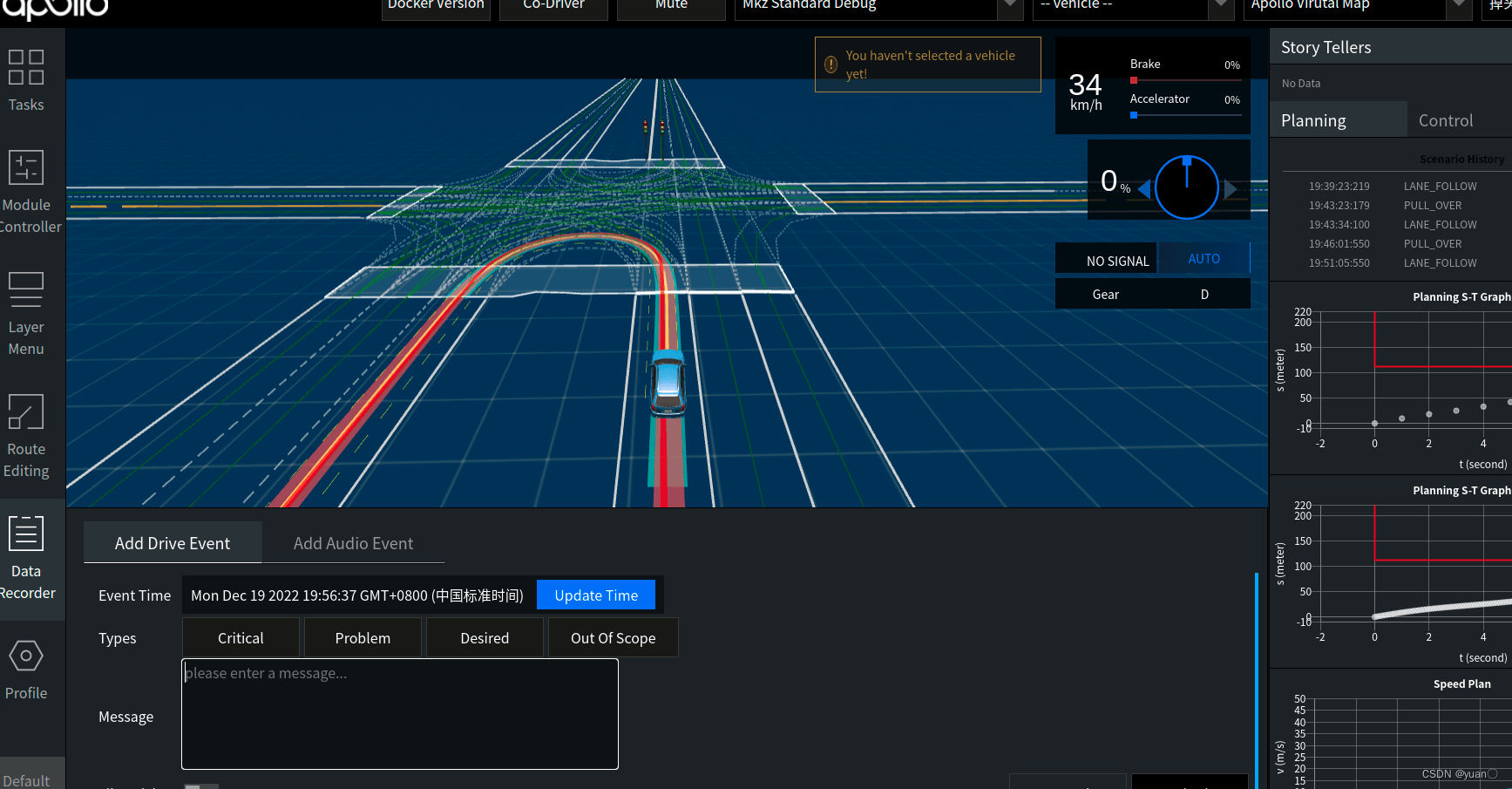
打开Data Recorder,将场景切换为掉头场景,接近弯道时点击Updata Time记录时间,场景运行结束后关闭planning模块
在云实验界面,点击Notebook打开jupyter
jupyter notebook

创建新的notebook,并输入
%matplotlib notebook
激活matplotlib
%matplotlib notebook
在jupyter notebook中运行以下命令打开对应时间的非线性规划的中间运行结果
/apollo/modules/planning/tools/plot_st_nlp.py
为绘图脚本文件的路径,
planning.INFO
为planning日志文件的路径,
23:29:03
为update更新的时间
run /apollo/modules/planning/tools/plot_st_nlp.py -f planning.INFO -t 23:29:03

有可能会出现这种状况

刷新几次,或将日志文件用其他方式打开(例如vim),当里面出现日志内容时,就可以了

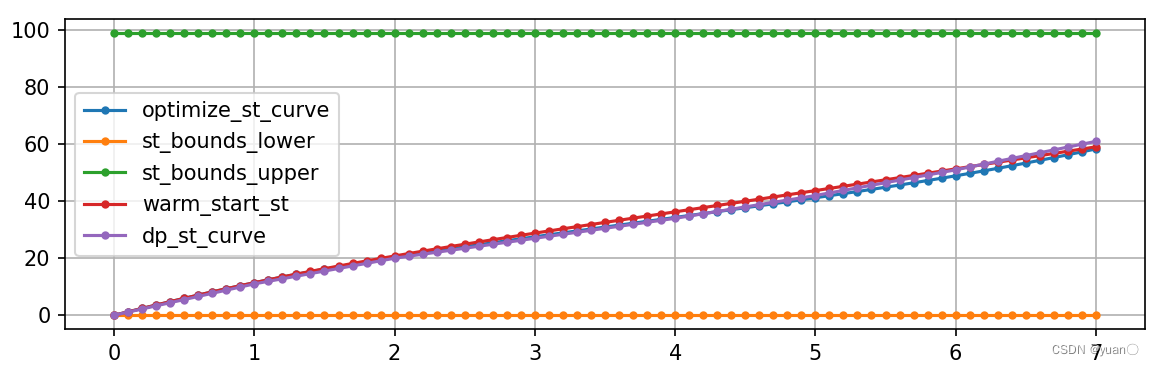
横坐标为
t
t
t
,纵坐标为
s
s
s
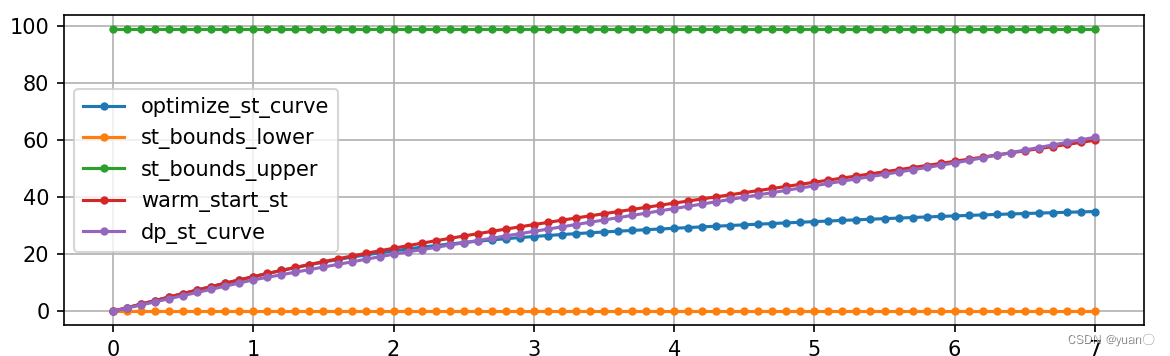
的ST图。橙色与绿色的线为边界。蓝色为规划出来的曲线。紫色为动态规划产生的曲线。红色为非线性规划平滑后的曲线
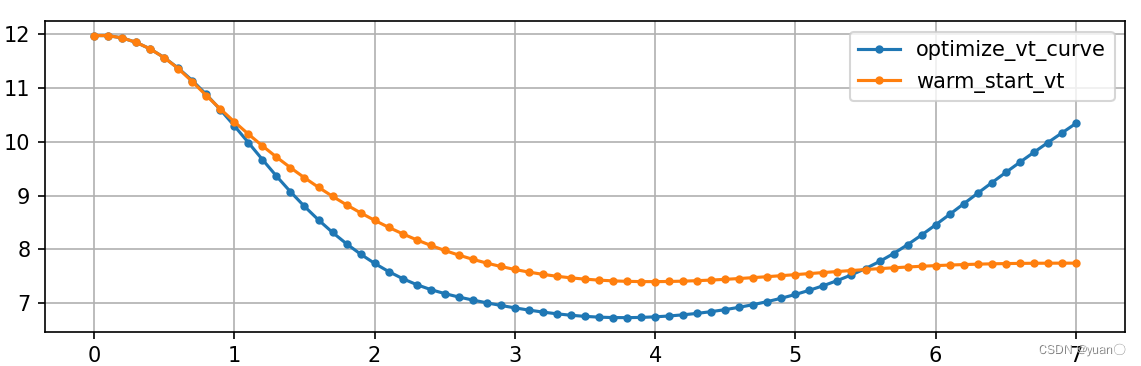
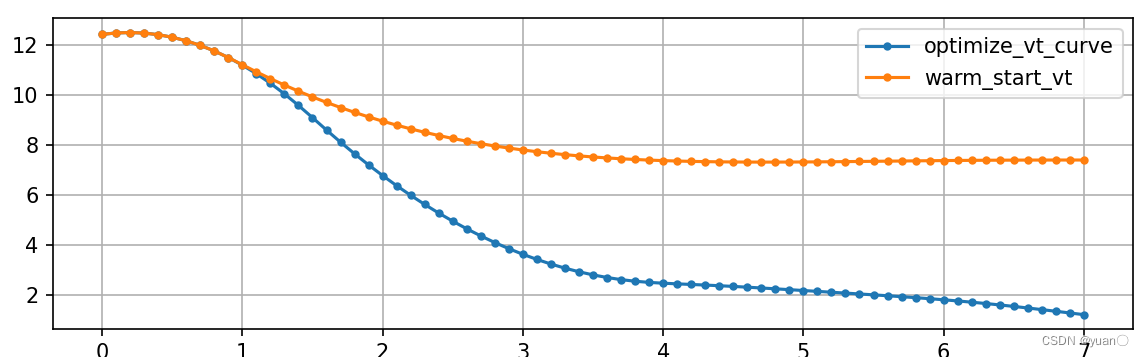
速度关于时间的曲线
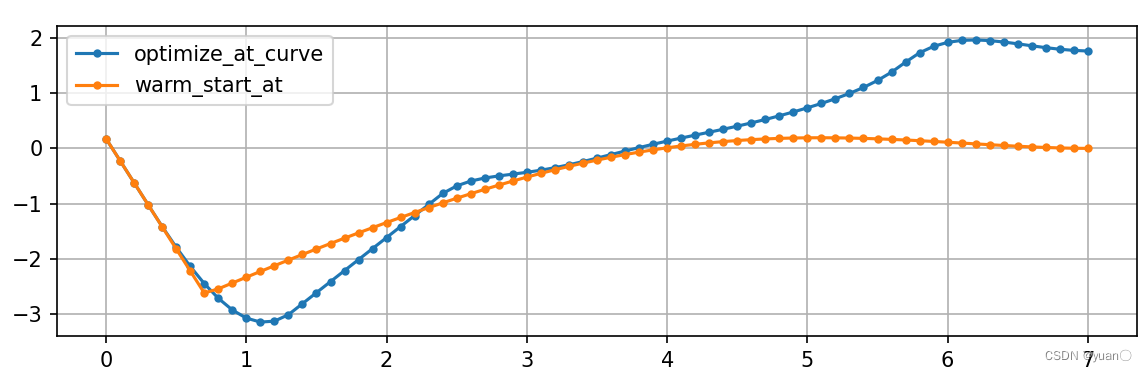
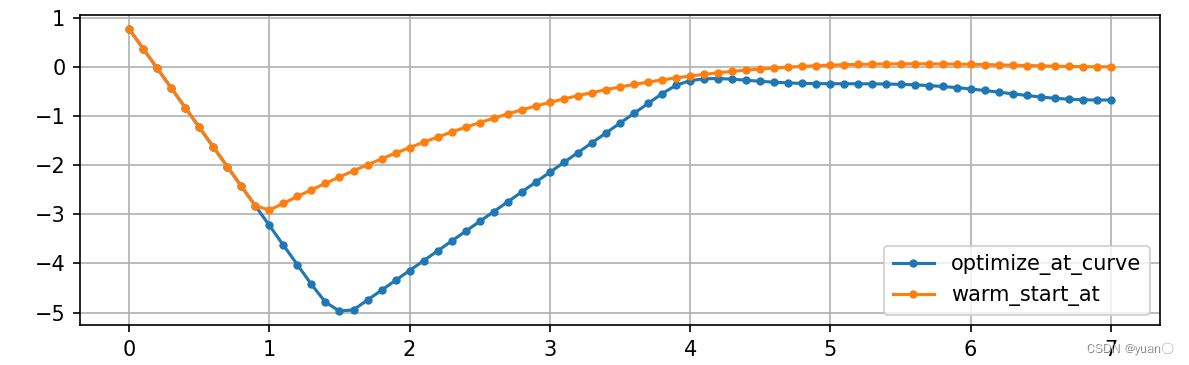
加速度关于时间的曲线
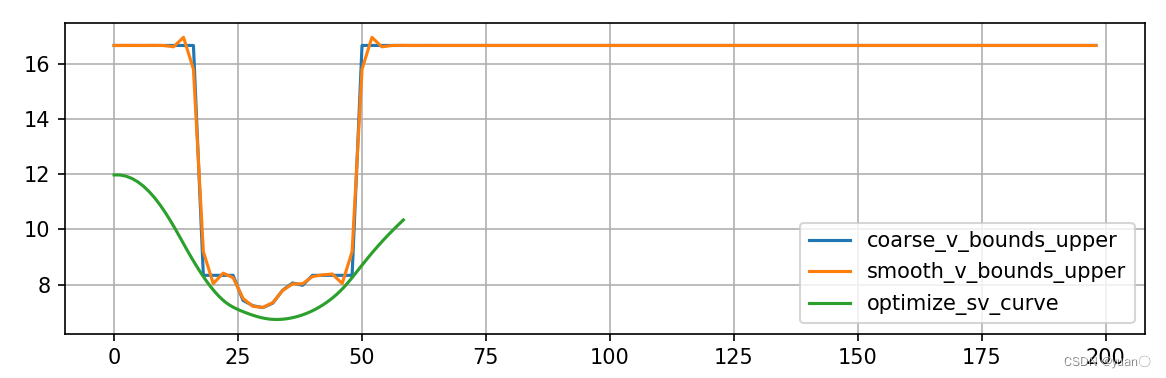
横坐标为
s
s
s
,纵坐标为
v
v
v
.可以看到通过弯道的速度还是很大的
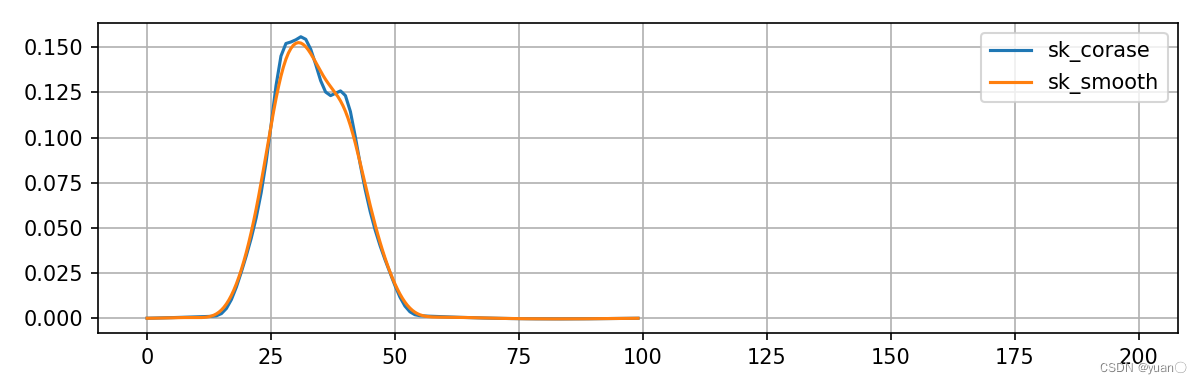
位置与kappa关系的曲线。橙色为规划平滑后的曲线。
通过点击下方-1 + 1来切换上-帧或下一帧速度规划数据

调高planning_ config.pb.txt文件中的横向加速度权重,重新打开planning模块运行掉头场景,观察修改后速度曲线变化
default_task_config: {
task_type: PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER
piecewise_jerk_nonlinear_speed_optimizer_config {
acc_weight: 2.0
jerk_weight: 3.0
lat_acc_weight: 10.0
s_potential_weight: 0.05
ref_v_weight: 5.0
ref_s_weight: 100.0
soft_s_bound_weight: 1e6
use_warm_start: true
}
}
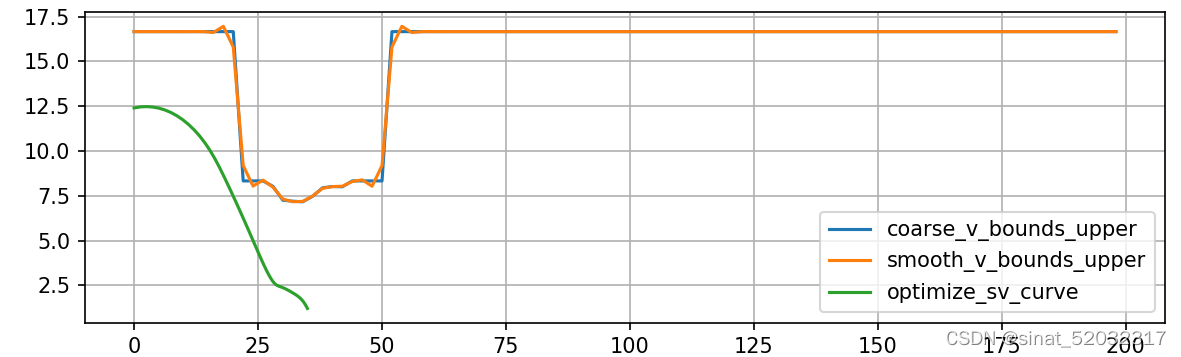
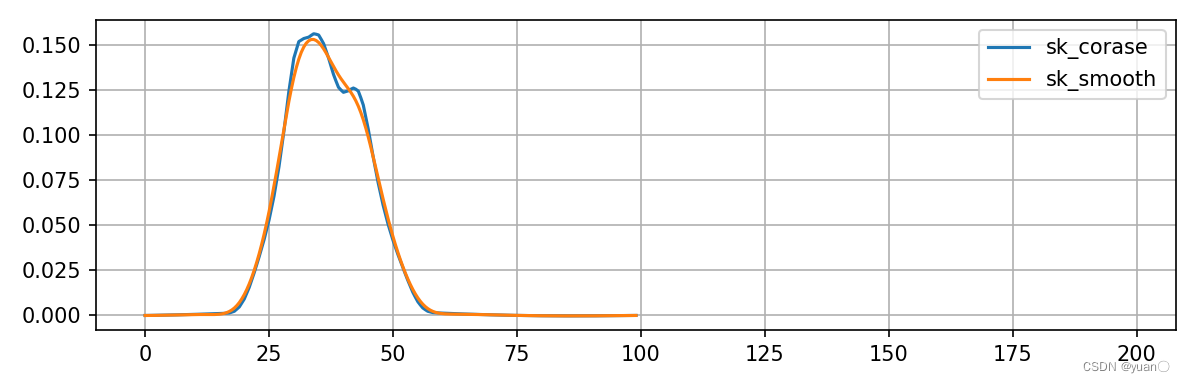
lat_acc_weight: 1000.0
5.3 通过减速带场景速度规划实践
打开planning模块,切换场景到减速带场景进行仿真,接近减速带时记录下时间,并通过plot st nlp.py脚本观察接近减速带时非线性规划算法的速度规划
在
lane_ follow config.pb.txt
文件中, 修改速度优化算法为QP算法,重新打开planning模块, 重新运行减速带场景,并记录接近减速带时的时间
stage_config: {
stage_type: LANE_FOLLOW_DEFAULT_STAGE
enabled: true
task_type: LANE_CHANGE_DECIDER
task_type: PATH_REUSE_DECIDER
task_type: PATH_LANE_BORROW_DECIDER
task_type: PATH_BOUNDS_DECIDER
task_type: PIECEWISE_JERK_PATH_OPTIMIZER
task_type: PATH_ASSESSMENT_DECIDER
task_type: PATH_DECIDER
task_type: RULE_BASED_STOP_DECIDER
task_type: SPEED_BOUNDS_PRIORI_DECIDER
task_type: SPEED_HEURISTIC_OPTIMIZER
task_type: SPEED_DECIDER
task_type: SPEED_BOUNDS_FINAL_DECIDER
task_type: PIECEWISE_JERK_SPEED_OPTIMIZER
#task_type: PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER
task_type: RSS_DECIDER
运行
plot_ st qp.py
,观察二次规划算法的速度 规划曲线在减速带区域速度规划和非线性规划算法有何区别。
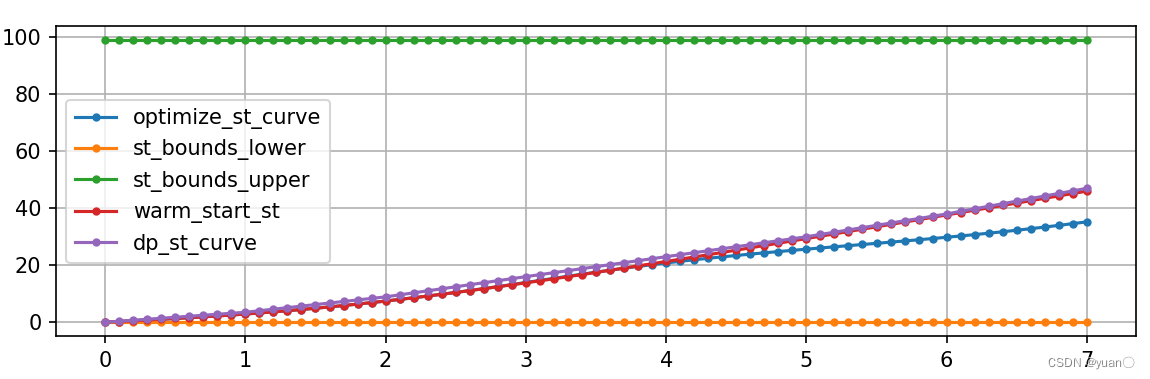
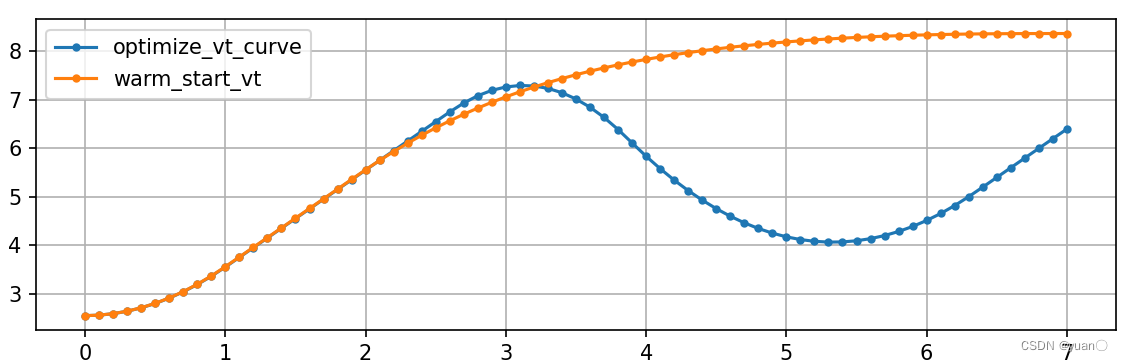
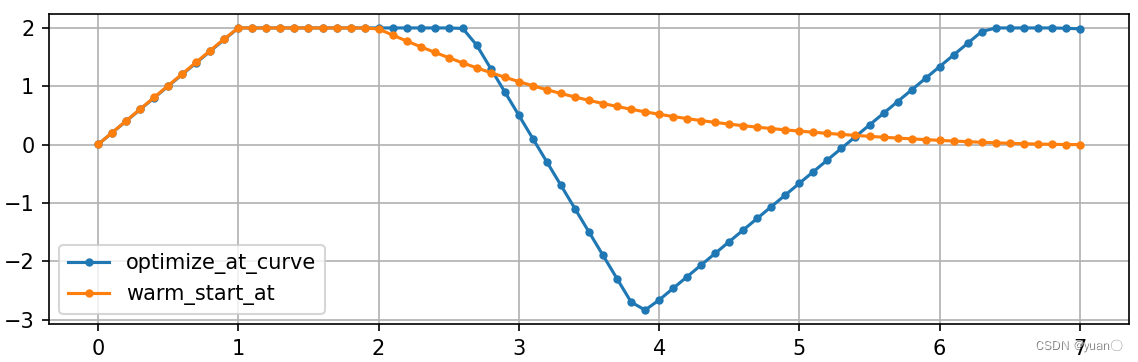
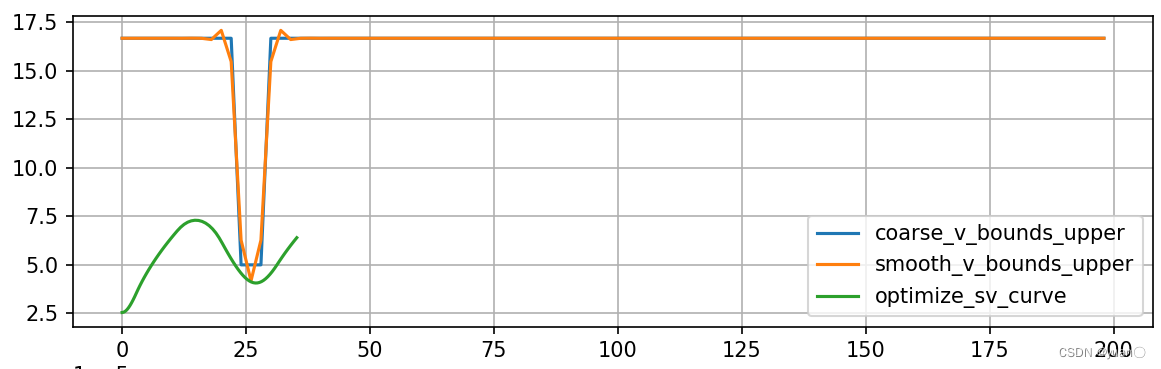
通过减速带的速度不超过5m/s.
非线性规划
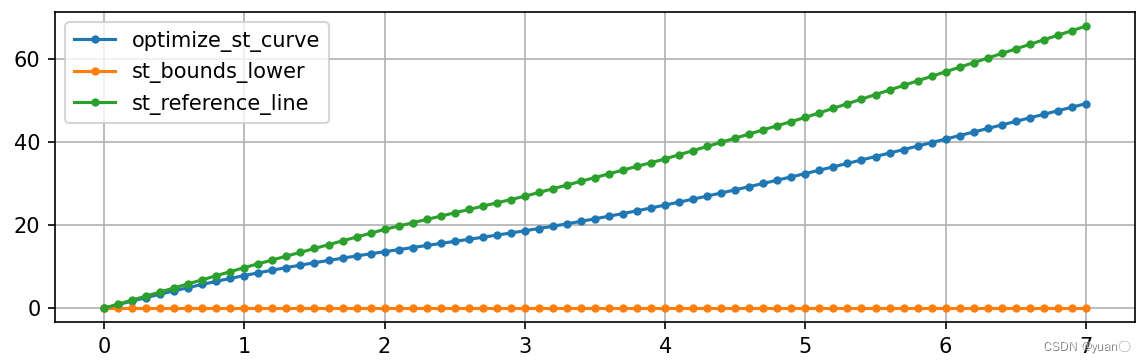
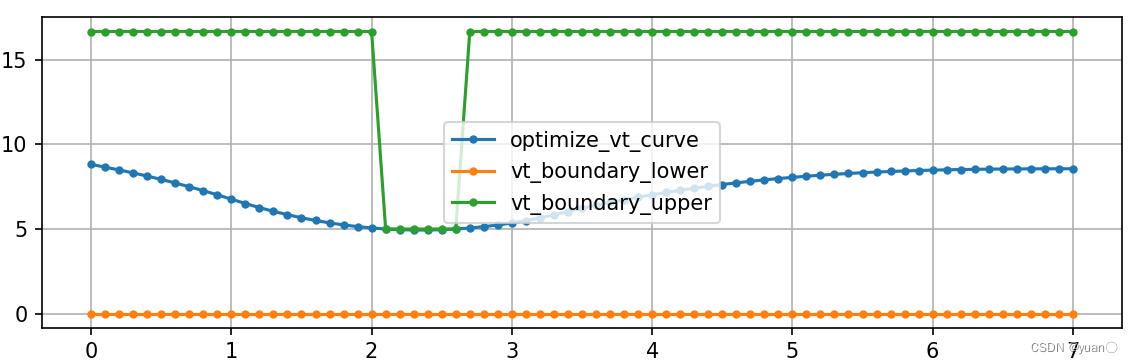
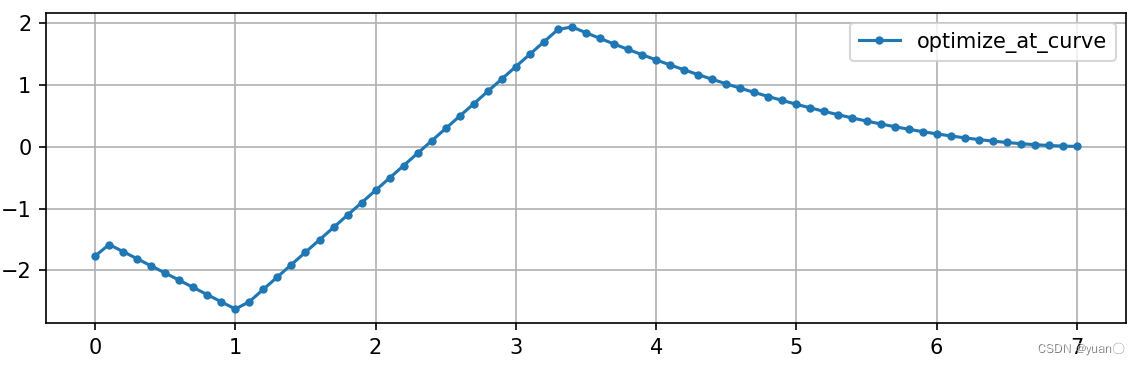
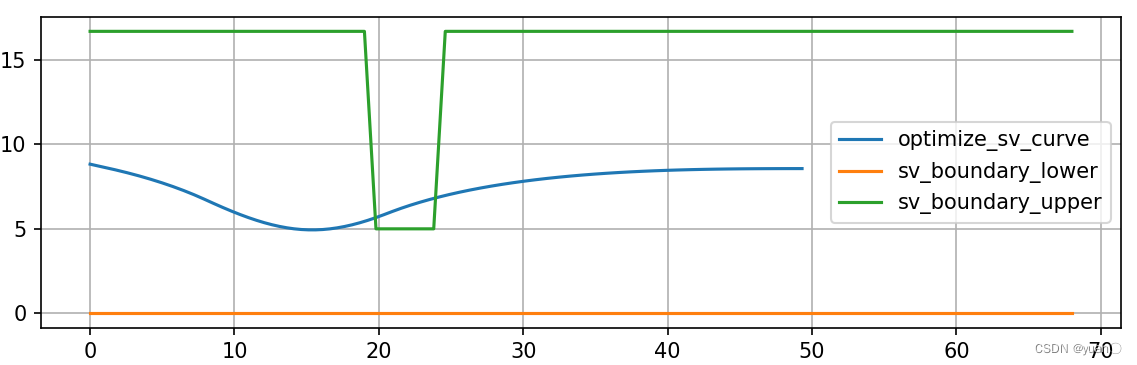
超出约束,算法的缺陷
二次规划
二次规划求解效率高,但不精确;非线性规划求解效率低,但精度高。