推荐系统笔记：基于非负矩阵分解的协同过滤 – 小飞侠

推荐系统笔记：基于非负矩阵分解的协同过滤

Post author:xfxia
Post published:2023年9月22日
Post category:其他

1 非负矩阵分解

非负矩阵分解 (NMF) 可用于非负的评级矩阵。这种方法的主要优势不一定是准确性，而是它

在理解用户-项目交互方面提供的高度可解释性。

与其他形式的矩阵分解的主要区别在于因子 U 和 V 必须是非负的。因此，非负矩阵分解中的优化公式表述如下：

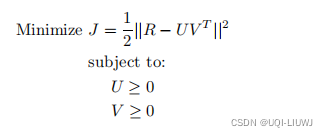
1.1 可解释性优势

尽管非负矩阵分解可用于任何非负评分矩阵（例如，评分从 1 到 5），但其最大的可解释性优势出现在

用户具有指定喜欢某一个条目，但不具有指定不喜欢某一个条目的机制。

这种矩阵包括一元评级矩阵，或其中非负条目对应于活动频率的矩阵。这些数据集也称为隐式反馈数据集。此类矩阵的一些示例如下：

在客户交易数据中，购买商品对应于表达对商品的喜好。然而，不购买商品并不一定意味着不喜欢，因为用户可能已经在别处购买了该商品，或者他们可能不知道该商品。当金额与交易相关联时，矩阵 R 可能包含任意非负数。但是，所有这些数字都指定了对某个项目的喜欢程度，但并不表示不喜欢。换句话说，隐式反馈中的数值表示置信度，而显式反馈中的数值表示偏好。（也就是说，此时的数值只是表示用户有“多可能”喜欢这件商品，并不是用户“有多喜欢”这件商品

与购买商品的情况类似，商品的浏览可以表示用户对商品的喜好。在某些情况下，购买或浏览行为的频率可以量化为非负值。

Facebook 上的“喜欢”按钮可以被视为一种为项目提供一元评级的机制。

2 一类协同过滤 one-class collaborative filtering

隐式反馈设置可以被认为是类似于分类和回归建模中的正未标记 (PU positive-unlabelled) 学习问题。在分类和回归建模中，当已知正类是一个非常小的少数类时，通过将未标记的条目视为属于负类，通常可以获得合理的结果。

类似地，此类矩阵和问题设置的一个有用方面是

将未指定条目设置为 0 ，

而不是将它们视为缺失值。这通常是合理的。

例如，考虑一个客户交易数据集，其中的值表示客户购买某一种商品的数量。在这种情况下，当客户没有购买该项目时，将值设置为 0 是合理的。

因此，在这种情况下，只需对完全指定的矩阵进行非负矩阵分解，这是机器学习中的一个标准问题。

这个问题也被称为一类协同过滤 one-class collaborative filtering。尽管最近的一些工作认为在这种情况下不应将缺失值设置为 0以减少偏差，但大量文献工作表明，

通过将缺少条目设置为 0，可以得到很稳健的结果。

当条目为 0 的先验概率非常大时尤其如此。

例如，在超市场景中，客户通常永远不会购买商店中的绝大多数商品。在这种情况下，将缺失值设置为 0（在初始矩阵中用于分解目的，而不是在最终预测中）将导致少量偏差，但明确地将初始矩阵中的条目视为未指定的条目将导致更大的解决方案复杂性。

不必要的复杂性总是导致过度拟合。这些影响在较小的数据集中尤为显着。

非负矩阵分解的优化公式是一种约束优化公式，可以使用标准方法（例如拉格朗日松弛法）求解。

数学知识笔记：拉格朗日乘子_UQI-LIUWJ的博客-CSDN博客

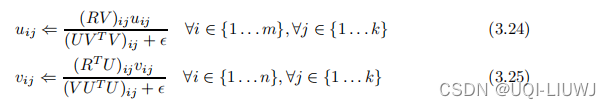
以下是推导部分（可能有些地方有问题，还望指教）

首先我们的目标函数为

$\left\{\begin{matrix} min \frac{1}{2}\sum_{(i,j)\in S} (r_{ij}-\sum_{p=1}^k u_{ip}v_{jp})^2 \\ u_{ip} \ge 0\\ v_{pj} \ge 0 \end{matrix}\right.$

那么我们构造如下的拉普拉斯函数

$\small L=\frac{1}{2}\sum_{(i,j)\in S} (r_{ij}-\sum_{p=1}^k u_{ip}v_{jp})^2 +\sum_{(i,j) \in S,p \in [1,k]}(\mu_p \times -u_{ip}) +\sum_{(i,j) \in S,p \in [1,k]}(\mu_p' \times -v_{pj})$

此时所有的μ和μ‘都是大于等于0的，且每一项μu,μ’v都为0

我们让L对
$\small u_{ij}$
求偏导，使得
$\small \frac{\partial L}{d u_{ij}}$
=0

我们先看L中和
$\small u_{ij}$
有关的项

$\small \frac{1}{2} (r_{i1}-\sum_{j=1}^k u_{ij}v_{1j})^2 +\frac{1}{2} (r_{i2}-\sum_{j=1}^k u_{ij}v_{2j})^2+\dots+\frac{1}{2} (r_{in}-\sum_{j=1}^k u_{ij}v_{nj})^2+(\mu_j\times -u_{ij})$

对其求偏导，有

$(r_{i1}-\sum_{j=1}^k u_{ij}v_{1j}) \times -v_{1j} +\dots+(r_{in}-\sum_{j=1}^k u_{ij}v_{nj}) \times -v_{nj}-\mu_j=0$

用矩阵的形式表述即为：

$(R-UV^T)_{i1} \times -V_{1j}+(R-UV^T)_{i2} \times -V_{2j}+\dots+(R-UV^T)_{in} \times -V_{nj}-\mu_j=0$

即

$[(R-UV^T)V]_{ij}+\mu_j=0$

我们又知道
$\mu_j \times u_{ij}=0$
，所以等号两边同时乘以
$\small u_{ij}$

有
$(RV)_{ij} u_{ij} =(UV^TV)_{ij} u_{ij}$

然后便可得到这个式子（加ε是为了不要除0）

【这里我在想，分母如果是RV+ε是不是也可以？就是分母分子调换一下？请评论区批评指正！】

V也同理

当然，我们也可以给非负矩阵分解的目标函数增加相应的正则项
$\frac{1}{2} \lambda_1||U||^2+\frac{1}{2}\lambda_2||V||^2$
。

此时的u，v更新式子更改为：

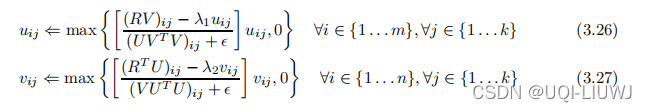
这里取max是为了保证u，v非负

3 非负矩阵分解的可解释性

类似于

推荐系统笔记：基于潜在因子模型的协同过滤（latent factor model）_UQI-LIUWJ的博客-CSDN博客

非负矩阵分解的主要优点是在解决方案中实现了高度的可解释性。

为了更好地理解这一点，请考虑一种情况，其中偏好矩阵包含客户购买的某种商品的数量。图 3.12 展示了一个具有 6 个商品和 6 个用户的 6×6 矩阵的示例。

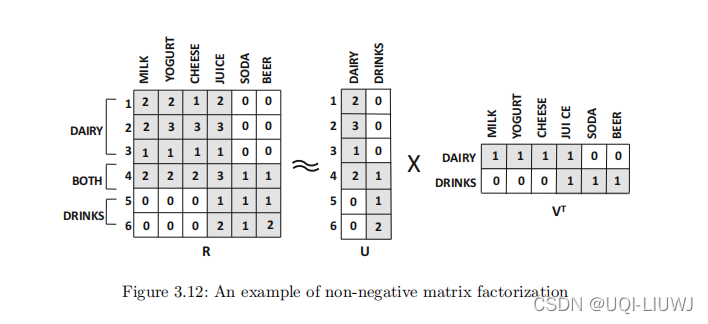
很明显，有两类产品分别对应于乳制品和饮料。

很明显，尽管所有客户似乎都喜欢果汁，但客户购买行为与商品类别高度相关。

我们记乳制品/饮料这些类别的项目为方面（aspect）。

相应的因子矩阵提供了关于客户和商品对这些方面的亲和力的清晰可解释性。

例如，客户 1 到 4 喜欢乳制品，而客户 4 到 6 喜欢饮料。这清楚地反映在 6 × 2 用户因子矩阵 U 中。数用户在两列中的每一列中的条目数量都量化了她对相关方面物品的兴趣水平。

同样，因子矩阵 V 显示了商品与各个方面的关系。因此，在这种情况下，条件

可以从 k = 2 个方面进行语义解释：

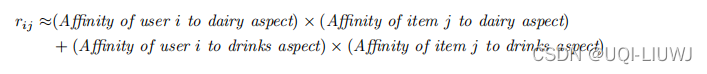
这种预测 rij 值的方法显示了矩阵的“部分总和”分解。（sum of parts）这也是

聚类问题经常使用非负矩阵分解

的原因之一。

在实际应用中，通常可以查看这些方面中的每一个，并从语义上解释用户和项目之间的关联。当语义标签可以手动附加到各种方面时，分解过程根据方面的各种语义，提供了对评级的简洁解释。

该“部分总和”分解可以用数学方式表示如下。通过分别用 U 和 V 的 k 列
$\bar{U_i}$
和
$\bar{V_i}$
表示矩阵乘积，可以将秩 k 矩阵分解
$UV^T$
分解为 k 个分量：

类似于

推荐系统笔记：无任何限制的矩阵分解_UQI-LIUWJ的博客-CSDN博客

每一个 m×n维矩阵
$\bar{U_i}\bar{V_i}^T$
都是一个秩1矩阵，对应相应的方面。

由于非负矩阵分解的可解释性，很容易将这些方面映射到不同集群cluster。

例如，上述例子的两个潜在成分分别对应于乳制品和饮料，如图 3.13 所示。

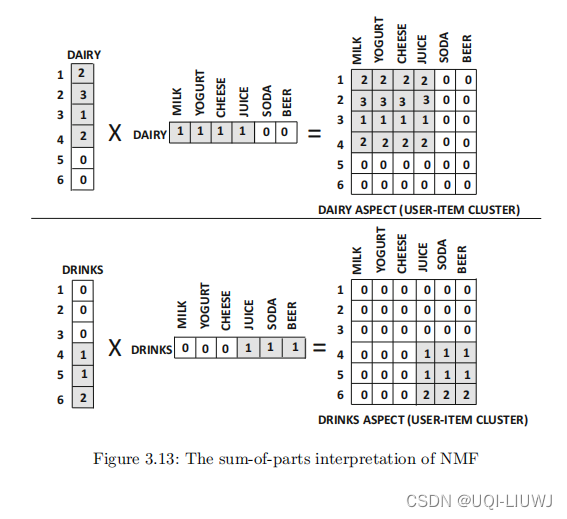
对于给定的 user-item 组合，评分预测是由不同方面的相应的user-item条目的和给出的

值得注意的是，方程 3.28 根据 U 和 V 的列进行分解。

而之前说的矩阵分解的方程
$r_{ij}=u_i v_j$
是根据 U 和 V 的行进行分解的不同方式。相当于两种理解方式。

4 关于隐式反馈分解的观察

第二小节我们说过隐式反馈分解。

非负矩阵分解特别适用于评级表示正偏好的隐式反馈矩阵。

与显式反馈数据集不同，由于此类数据中

缺少负反馈

，因此无法忽略优化模型中缺失的条目。值得注意的是，非负矩阵分解模型通过

将缺失条目设置为 0 将它们视为负反馈

。不这样做会严重增加未观察到的条目的错误。

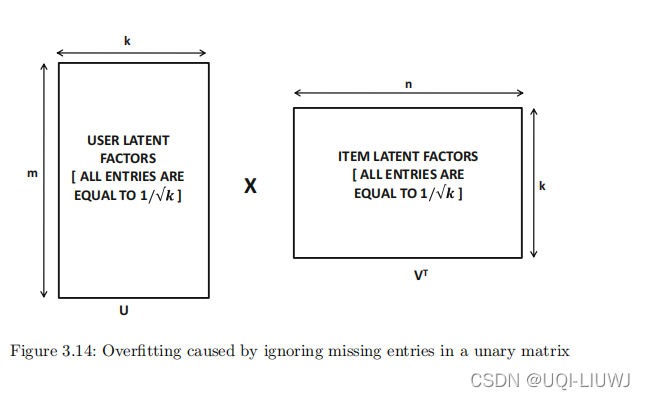
为了理解这一点，请考虑一个一元评级矩阵，其中喜欢由 1 指定。图 3.14 中所示的是这个一元评级矩阵的矩阵分解结果。

如果仅对有数值的条目进行误差比较时，在任意一元矩阵上这样的分解都能提供 100% 的准确度。这是因为图 3.14 中 U 和
$V^T$
的乘法导致矩阵只包含 1 且没有 0。

当然，这样的分解对于未观察到的条目会有非常高的误差，因为许多未观察到的条目可能对应于负面偏好。

这个例子是

缺乏负反馈数据导致过拟合的表现

。

因此，对于缺失负面偏好、并且负面偏好远远超过正面偏好的评分矩阵，比较重要的步骤是将缺失的条目视为 0。

例如，在客户交易数据集中，如果这些值表示不同用户购买的数量，并且大多数商品默认没有购买，则可以将缺失条目的值近似为 0。

5 同时给喜欢&不喜欢打分的矩阵

到目前为止，我们对非负矩阵分解的讨论仅集中在隐式反馈矩阵上，即

用户具有指定喜欢某一个条目，但不具有指定不喜欢某一个条目的机制。

现在我们考虑同时表示喜欢和不喜欢的矩阵。尽管可以对名义上的非负评级（例如，从 1 到 5，1 表示非常不喜欢，5表示非常喜欢）使用非负矩阵分解，但在这种情况下使用非负矩阵分解没有特殊的可解释性优势。

在这种情况下，

不能将未指定的条目视为 0，并且只能使用有观测数据的那些条目

。

和之前一样，我们也记S为我们所有有观测数值的(i,j)对的集合

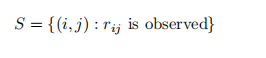
相应的目标函数（带正则化项）如下：

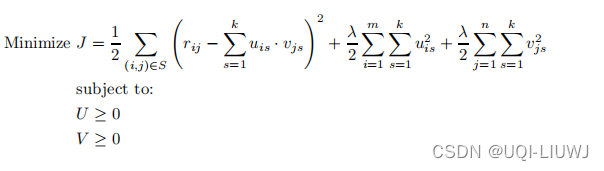
该公式类似于无约束矩阵分解中的正则化公式。唯一的区别是添加了非负约束。确保U,V在更新期间保持非消极性。

如果 U 或 V 的任何分量因更新而违反非负约束，则将其设置为 0。

与所有随机梯度下降方法一样，执行更新直到收敛。

在评级可以同时指定喜欢和不喜欢的设置中，非负矩阵分解在可解释性方面比无约束矩阵分解

没有特殊优势

。这是因为人们无法再从部分总和的角度来解释解决方案。例如，三个不喜欢评级的相加不能解释为导致喜欢评级。

版权声明：本文为qq_40206371原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/qq_40206371/article/details/122152700