研究机械臂的正向运动学需要从机械臂的变换矩阵开始。
变换矩阵可以说有两种形式,一种产生了标准D-H参数,另一种产生了改进D-H参数表。
标准D-H参数——变换矩阵
引用一些博客的图片,以及我多次的试验,在这里记下来。
在此之前,需要重点强调的是,无论是标准D-H参数法还是改进D-H参数法,
我们都是使用矩阵右乘的法则:
在下面提到的变换的四个过程中,比如有两个坐标系,一个是
初始坐标i
,一个是
目的坐标系j
。我们会设定一个作为中间转换过程的坐标系A,一开始这个坐标系A是与初始坐标i重合。我们仔细留意一下,**就知道下面的每一次转化都是在运动的坐标A或者是最后的坐标系j来进行的。**这样就呼应了右乘的方法。
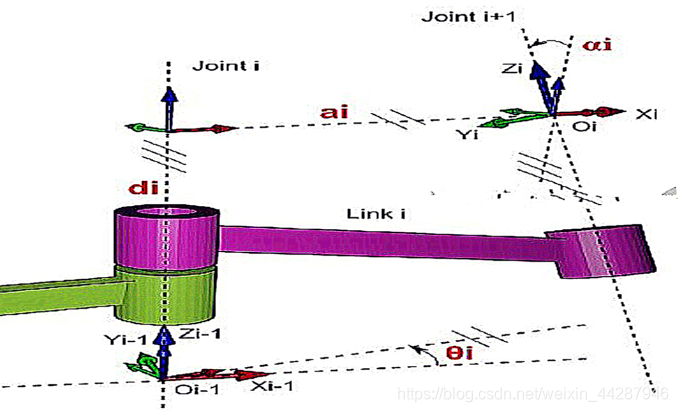
标准D-H参数法的变换矩阵的顺序是,
按照Z-X的顺序:
①
先绕坐标系i的Z轴旋转θ角,该值便为θ1。使得Xi轴与Xj轴平行。——
先绕坐标系A的轴旋转θ角,使得XA与Xj平行。
一样的功能,破折号前是简便的说法。
②
在沿着坐标系i的Z轴,将Xi轴移动D1的距离,与Xi轴与Xj重合。——
沿着坐标系A的Z轴,将XA移动D1的距离
,
这里就可以清晰理解,坐标系i其实是没动过的,动的只是坐标系A,而坐标j也算是运动的坐标系
③
接着绕着坐标系j的Xj轴(同时也是Xi轴,应为此前已经重合了),旋转α角,该值为α1。——
现在到绕这坐标系A的X轴旋转了
④
最后便是沿着坐标系j的Xj轴,将坐标系i的Zi轴平移a1的距离。
这样一来便可以产生一个连杆,这个连杆可以命名为LINK(I);
最最最重要的一步是:
上面有四个步骤,每个步骤都可以写出一个齐次坐标矩阵(4
4),
由于使用的是矩阵右乘,来求出末端相对于参考系的位姿,(我的理解是在正向运动学中,末端是未知,是运动的。只能设置每个的关节的角度,按照矩阵乘法的概念),可以写成:
T1=ROT(θ)Trans(D1)ROT(α)Trans(a1),
然后就是有末端执行器的[xj,yj,zj,1]T=T1
[xi,yi,zi,1]。
最后上面的四个变换便可以写成一个公式,(在MATLAB上找到证据)

如果是标准D-H参数的话,就选第一个作为计算正向运动的式子,如果是改进D-H参数,就选择第二个。
假设我有一个六自由度的机械臂,那么就有六个这样的矩阵,
①号关节-②号
②号——③号
③号——④号
④号——⑤号
⑤号——⑥号
⑥号——工具(最末端的坐标系)
这样子,利用这些矩阵便可以求出末端执行器相对于基坐标的位姿。
公式是这样的:
i2=T(1-2)*i1..............
最后变换便可以得到
iE=T(1-2)T(2-3)T(3-4)T(4-5)T(5-6)T(6-E)i0,(当然这个公式是基于基坐标系的,参考坐标系不同,公式就会不同。
为此我也在Matlab上验证了一下。
L1 = Link([0 348.5 0 pi/2 ],‘standard’);%1 2
L2 = Link([0 0 284.5 0 ],‘standard’);%2 3
L3 = Link([0 0 30 pi/2 ],‘standard’);%3 4
L4 = Link([0 286.5 0 -pi/2 ],‘standard’);%4 5
L5 = Link([0 0 0 pi/2 ],‘standard’);%5 6
L6 = Link([0 81.5 0 0 ],‘standard’);%6 和末端执行器
robot = SerialLink([L1 L2 L3 L4 L5 L6 ],‘name’, ‘my robot’);
%robot.plot([0 0 0 0 0 0 ]);
teach(robot);
display(robot);
theta1=0;
theta2=0;%
theta3=0;
theta4=0;
theta5=0;
theta6=0;
q=[theta1 theta2 theta3 theta4 theta5 theta6];
T=robot.fkine(q);
robot.plot(q);
a2= L2.a;
a3= L3.a;
d1= L1.d;
d4= L4.d;
d6= L6.d;
s1=sin(0);
c1=cos(0);
s2=sin(0);
c2=cos(0);
s3=sin(0);
c3=cos(0);
s4=sin(0);
c4=cos(0);
s5=sin(0);
c5=cos(0);
s6=sin(0);
c6=cos(0);
T1=[c1 0 s1 0; s1 0 -c1 0; 0 1 0 d1; 0 0 0 1;]%1-2
T2=[c2 -s2 0 a2*c2; s2 c2 0 a2*s2; 0 0 1 0; 0 0 0 1;] %2-3
T3=[c3 0 s3 a3*c3; s3 0 -c3 a3*s3; 0 1 0 0; 0 0 0 1;]%3-4
T4=[c4 0 -s4 0; s4 0 c4 0; 0 -1 0 d4; 0 0 0 1;]%4-5
T5=[c5 0 s5 0; s5 0 -c5 0; 0 1 0 0; 0 0 0 1;]%5-6
T6=[c6 -s6 0 0; s6 c6 0 0; 0 0 1 d6; 0 0 0 1;]%6-7
Tz=T1*T2*T3*T4*T5*T6
我用的自己设计一款高仿机械臂,朋友们可以参考我的一篇博客,里面有介绍一些的详细的数据,经过验证,是正确的。
关于书籍的内容,
蔡自兴教授有编写过一版书
在介绍变换矩阵时,介绍了标准D-H参数法对应的变换方法和顺序,但是在后面介绍PUMA560时,用的是改进D-H参数对应的变换方法和顺序,以及他的公式。(我发现)
后来又看了一版书,教授使用的都是改进D-H参数,我觉得是这样的,不知到大家有没有发现。