前面一篇由于文字太多,不给编辑,遂此篇出炉
LEETCODE-刷题个人笔记 Python(1-400)-TAG标签版本(一)
DFS&BFS
(262)200. Number of Islands(Medium)
给定1d(陆地)和’0’(水)的2d网格图,计算岛屿数量。岛被水包围,通过水平或垂直连接相邻的土地而形成。
您可以假设网格的所有四个边都被水包围。
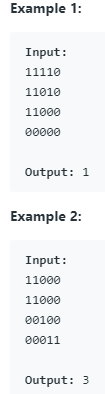
思路:
1、使用dfs
2、如果此处是1的话,就把周边所有1 换成X,防止再次访问(多个相邻的1只能当作一个岛屿)
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
def sink(i, j):
if 0 <= i < len(grid) and 0 <= j < len(grid[i]) and grid[i][j] == '1':
grid[i][j] = 'X'
map(sink, (i+1, i-1, i, i), (j, j, j+1, j-1))
return 1
return 0
return sum(sink(i, j) for i in range(len(grid)) for j in range(len(grid[i])))
(263)286 Walls and Gates(Medium)
您将获得使用这三个可能值初始化的m x n 2D网格。
-1 – 墙壁或障碍物。
0 – 门
INF – Infinity意味着一个空房间。
每个空房间填充距离最近的门的距离。如果无法到达大门,则应填充INF。

思路:
只有当当前值大于上一值+1时,我们才递归,从而更新;其他情况我们不需要更新,所以也不需要递归
def wallsAndGates(rooms):
def dfs(x,y):
for i,j in [[-1,0],[1,0],[0,-1],[0,1]]:
if 0<=i+x<m and 0<=j+y<n and rooms[x+i][y+j]>0:
if rooms[x+i][y+j]>rooms[x][y]+1:
rooms[x+i][y+j] = rooms[x][y]+1
dfs(x+i,y+j)
if not rooms:
print(rooms)
m = len(rooms)
n = len(rooms[0])
for i in range(m):
for j in range(n):
if rooms[i][j]==0:
dfs(i,j)
(264)130. Surrounded Regions(Medium)
给定包含“X”和“O”(字母O)的2D板,捕获由“X”包围的所有区域。 通过将所有’O’翻转到该周围区域中的’X’来捕获区域。

思路:
1、先看边界,边界有O加入stack中
2、然后取出stack中的元素,改为S,如果其上下左右有O,则加入stack,直到stack中没有点为止
3、最后将2D板中不是S的元素全部改为X
def solve(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
m = len(board)
if m==0:
return
n = len(board[0])
stack = []
for i in range(n):
if board[0][i]=='O':
stack.append([0,i])
if board[m-1][i]=='O':
stack.append([m-1,i])
for i in range(1,m-1):
if board[i][0] =='O':
stack.append([i,0])
if board[i][n-1]=='O':
stack.append([i,n-1])
while stack:
pos = stack.pop(0)
board[pos[0]][pos[1]] = 'S'
if pos[0]>0 and board[pos[0]-1][pos[1]] =='O':
stack.append([pos[0]-1,pos[1]])
if pos[0]<m-1 and board[pos[0]+1][pos[1]] =='O':
stack.append([pos[0]+1,pos[1]])
if pos[1]>0 and board[pos[0]][pos[1]-1] =='O':
stack.append([pos[0],pos[1]-1])
if pos[1]<n-1 and board[pos[0]][pos[1]+1] =='O':
stack.append([pos[0],pos[1]+1])
for i in range(m):
for j in range(n):
if board[i][j]=='S':
board[i][j]='O'
else:
board[i][j]='X'
(265)339 Nested List Weight Sum(Easy)
给定嵌套的整数列表,返回列表中所有整数的总和,加权深度。 每个元素都是整数或列表 – 其元素也可以是整数或其他列表。
Example 1:
Given the list [[1,1],2,[1,1]], return 10. (four 1’s at depth 2, one 2 at depth 1)
Example 2:
Given the list [1,[4,[6]]], return 27. (one 1 at depth 1, one 4 at depth 2, and one 6 at depth 3; 1 + 4
2 + 6
3 = 27)
思路:
嵌套整数链表的加权求和。这个结构里面有整数也有链表,整数的话就乘上深度返回,而是链表的话就进入下一层继续遍历。
我们可以很容易的由嵌套想到递归解决这个问题,类似于深度优先遍历。
学会使用
isinstance
class Solution:
def depthSum(self,nestedList):
self.res = 0
def dfs(arr, depth):
for i in arr:
if isinstance(i,int):
self.res +=i*depth
else:
dfs(i,depth+1)
dfs(nestedList,1)
print(self.res)
a = Solution()
a.depthSum([[1,1],2,[1,1]])
(266)364 Nested List Weight Sum II(Medium)
嵌套整数链表的加权求和。这个结构里面有整数也有链表,整数的话就乘上深度返回,而是链表的话就进入下一层继续遍历。
与之前的问题不同,重量从根到叶增加,现在权重是从下到上定义的。即,叶级整数具有权重1,并且根级整数具有最大权重。

思路:
先记录下来每一层的元素,最后递归出来之后在相加乘以权重
def depthSumInverse(nestedList):
int sum = 0
res = []
dfs(nestedList,0,res)
for i in range(1,len(res)+1):
sum +=i*res[len(res)-i]
return sum
def dfs(nestedList,depth,res):
if depth == len(res):
res.append([0])
for a in nestedList:
if isinstance(int,a):
res[depth] += a
else:
dfs(nestedList,depth+1,res)
(267)126. Word Ladder II(Hard)
给定两个单词(beginWord和endWord)和一个字典的单词列表,找到从beginWord到endWord的所有最短变换序列
Input:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
Output:
[
[“hit”,“hot”,“dot”,“dog”,“cog”],
[“hit”,“hot”,“lot”,“log”,“cog”]
]
思路:
难题,据说是通过率最小的题
使用dfs一个个找和某个单词相关的(即相差一个字符的)然后存入字典,每次更新字典
1、使用new_layer来记录下一层要用的
2、将所有只差一个字母的存到new_layer中,将new_layer赋值给layer
def findLadders(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: List[List[str]]
"""
wordList = set(wordList)
res = []
layer = {}
layer[beginWord] = [[beginWord]]
#如果endWord不在List中,则直接退出
if endWord not in wordList:
return res
while(layer):
#用一个新的层来记录下一步的layer
new_layer = collections.defaultdict(list)
for w in layer:
if w ==endWord:
res.extend(i for i in layer[w])
else:
#将所有和w只差一个字母的存起来
for i in range(len(w)):
for c in 'abcdefghijklmnopqrstuvwxyz':
w1 = w[:i]+c+w[i+1:]
#如果在list找到了,就添加到new_layer中
if w1 in wordList:
new_layer[w1] += [j+[w1] for j in layer[w]]
#将所有已经用过的词删除(找出最短的)
wordList -=set(new_layer.keys())
layer = new_layer
print(layer)
return res
(268)127. Word Ladder(Medium)
给定两个单词(beginWord和endWord)和一个字典的单词列表,找到从beginWord到endWord的最短变换序列的长度
思路:只会用和126一样的方式,不过运行速度有点慢
def ladderLength(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: int
"""
wordList = set(wordList)
res = []
layer = {}
layer[beginWord] = [[beginWord]]
if endWord not in wordList:
return 0
while(layer):
new_layer = collections.defaultdict(list)
for w in layer:
if w ==endWord:
res.extend(i for i in layer[w])
return len(res[0])
else:
for i in range(len(w)):
for c in 'abcdefghijklmnopqrstuvwxyz':
w1 = w[:i]+c+w[i+1:]
if w1 in wordList:
new_layer[w1] += [j+[w1] for j in layer[w]]
wordList -=set(new_layer.keys())
layer = new_layer
return 0
51 52. N-Queens(Hard)
思路:用DFS实现,重要的是定义一个index,循环一次nums[index] == i
还有一个判断条件,斜对角绝对值之差!=index-i
定义一个1维长度为n的向量,用来存储列的值
(269)51. N-Queens(Hard)
给定整数n,返回n-queens拼图的所有不同解。
思路:(只需要一维的向量)
1、(判断斜对角没有那么简单)
abs(nums[i]-nums[n])==n-i
2、可以每一行的添加元素,这样就只需要一个循环,而且不用判断每一行有没有一样的
3、可以使用递归来做
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
def is_vaild(nums,n):
for i in range(n):
if abs(nums[i]-nums[n])==n-i or nums[i]==nums[n]:
return False
return True
def dfs(nums,path,index):
if len(nums)==index:
res.append(path)
return
for i in range(len(nums)):
nums[index] = i
if is_vaild(nums,index):
temp = '.'*len(nums)
dfs(nums,path+[temp[:i]+'Q'+temp[i+1:]],index+1)
nums = [0]*n
res = []
dfs(nums,[],0)
return res
(270)52. N-Queens II(Hard)
给定整数n,返回n-queens拼图的不同解的数量。
思路:和51的思路一样,但是无需存储路径
def totalNQueens(self, n):
"""
:type n: int
:rtype: int
"""
def is_vaild(nums,index):
for i in range(index):
if abs(nums[i]-nums[index])==index-i or nums[i]==nums[index]:
return False
return True
def dfs(nums,index):
if index ==len(nums):
self.res +=1
return
for i in range(len(nums)):
nums[index] = i
if is_vaild(nums,index):
dfs(nums,index+1)
nums = [0]*n
self.res = 0
dfs(nums,0)
return self.res
Stack & PriorityQueue
(271)155. Min Stack(Easy)
设计一个支持push,pop,top和在恒定时间内检索最小元素的堆栈。
push(x) – 将元素x推入堆栈。
pop() – 删除堆栈顶部的元素。
top() – 获取顶部元素。
getMin() – 检索堆栈中的最小元素。
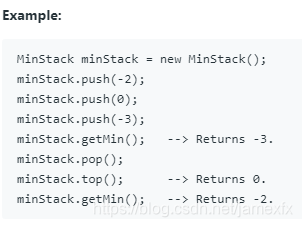
思路:
每次存的时候,同时看一下最小值是哪一个,并把x和最小值同时存储
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.q = []
def push(self, x):
"""
:type x: int
:rtype: void
"""
curmin = self.getMin()
if curmin==None or curmin>x:
curmin = x
self.q.append([x,curmin])
def pop(self):
"""
:rtype: void
"""
return self.q.pop()
def top(self):
"""
:rtype: int
"""
if len(self.q)==0:
return None
else:
return self.q[-1][0]
def getMin(self):
"""
:rtype: int
"""
if len(self.q)==0:
return None
else:
return self.q[-1][1]
(272)232 Implement Queue using Stacks(Easy)
使用堆栈实现队列的以下操作。
push(x) – 将元素x推送到队列的后面。
pop() – 从队列前面删除元素。
peek() – 获取前面的元素。
empty() – 返回队列是否为空。
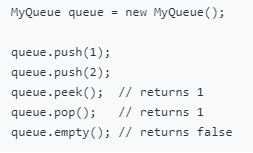
思路:
使用两个stack,一个用来存储,一个用来pop,当s2为空的时候,把s1中的结果放入s2中。加入元素的时候把元素加入s1中。
class MyQueue:
def __init__(self):
self.s1 = []
self.s2 = []
def push(self, x):
self.s1.append(x)
def pop(self):
self.peek()
return self.s2.pop()
def peek(self):
if not self.s2:
while self.s1:
self.s2.append(self.s1.pop())
return self.s2[-1]
def empty(self):
return not self.s1 and not self.s2
(273)225 Implement Stack using Queues(Easy)
使用队列实现堆栈的以下操作。
push(x) – 将元素x推入堆栈。
pop() – 删除堆栈顶部的元素。
top() – 获取顶部元素。
empty() – 返回堆栈是否为空。
思路:
只用使用一个queue就行,在放进一个元素之后,其它元素再往后面放
import collections
class Stack:
# initialize your data structure here.
def __init__(self):
self.stack = collections.deque([])
# @param x, an integer
# @return nothing
def push(self, x):
self.stack.append(x)
# @return nothing
def pop(self):
for i in range(len(self.stack) - 1):
self.stack.append(self.stack.popleft())
return self.stack.popleft()
# @return an integer
def top(self):
return self.stack[-1]
# @return an boolean
def empty(self):
return len(self.stack) == 0
(274)71. Simplify Path(Medium)
给定文件的绝对路径(Unix风格),简化它。或者换句话说,将其转换为规范路径。
请注意,返回的规范路径必须始终以斜杠/开头,并且两个目录名之间必须只有一个斜杠/。最后一个目录名称(如果存在)不得以尾随/结尾。
Input: “/a//bc/d//././/…”
Output: “/a/b/c”
先将绝对路径按照’/‘分开,然后利用stack
def simplifyPath(self, path):
"""
:type path: str
:rtype: str
"""
p = [i for i in path.split('/') if i!='' and i!='.']
res =[]
for i in p:
if i =='..':
if res ==[]:
continue
else:
res.pop()
else:
res.append(i)
return '/'+'/'.join(res)
(275)388 Longest Absolute File Path(Medium)
假设我们通过以下方式用字符串抽象我们的文件系统:
The string “dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext” represents:
给定以上述格式表示文件系统的字符串,返回抽象文件系统中文件的最长绝对路径的长度。如果系统中没有文件,则返回0。
Note:
The name of a file contains at least a . and an extension.
The name of a directory or sub-directory will not contain a …
Notice that a/aa/aaa/file1.txt is not the longest file path, if there is another path aaaaaaaaaaaaaaaaaaaaa/sth.png.
思路:
定义最大长度的max_len. 定义字典,用来存储当前深度的累计长度
使用for循环,/n当作分隔符
去除掉最前面的/t
去除的/t的数量代表深度的情况
如果当前name中含有‘.’的话,就更新max_len
否则使用字典存储当前长度(覆盖模式)
def lengthLongestPath(self, input):
"""
:type input: str
:rtype: int
"""
max_len = 0
dict = {0:0}
for line in input.split('\n'):
name = line.lstrip('\t')
depth = len(line) - len(name)
if '.' in name:
max_len = max(max_len,dict[depth] + len(name))
else:
dict[depth+1] = dict[depth] + len(name) +1
return max_len
(276)394 Decode String(Medium)
给定编码字符串,返回其解码字符串。 编码规则是:k [encoded_string],其中方括号内的encoded_string正在重复k次。注意,k保证是正整数。您可以假设输入字符串始终有效;没有多余的空白区域,方括号格式正确等。此外,您可以假设原始数据不包含任何数字,并且该数字仅用于那些重复数字k。例如,不会有像3a或2 [4]这样的输入。
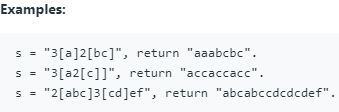
思路:
使用stack进行存储,用num来存储数字(大于两位数需要考虑,所以使用+=)
如果是数字:则num += char
如果是’[’,stack就加入一个元素[’’,int(num)],并且将num设为空字符
如果是‘]’, stack就stack中弹出最后一个,然后将其stack中的最后一个的字符中
如果是子母的话,则直接添加到stack[-1][0]中
def decodeString(self, s):
"""
:type s: str
:rtype: str
"""
stack = [['',1]]
num = ''
for char in s:
if char.isdigit():
num += char
elif char =='[':
stack.append(['',int(num)])
num = ''
elif char ==']':
s,k = stack.pop()
stack[-1][0] += s*k
else:
stack[-1][0] +=char
return stack[0][0]
(277)224 Basic Calculator(Hard)
实现基本计算器来评估简单的表达式字符串。 表达式字符串可以包含open(和右括号),加号或减号 – ,非负整数和空格。
这个问题就是要了解以下内容: 输入始终包含有效字符串 加法和减法的规则 括号的优先含义 空格不会影响输入表达式的评估。
Input: “(1+(4+5+2)-3)+(6+8)”
Output: 23
思路:
使用stack,因为负号不满足交换算法B-C != C-B,所以使用B+(-C)来表示
每次要判断前面是什么符号,然后使用sign来保存,然后存入stack中
def calculate(s):
"""
:type s: str
:rtype: int
"""
stack = []
operand = 0
res = 0
sign = 1
for ch in s:
if ch.isdigit():
operand = (operand * 10) + int(ch)
elif ch == '+':
res += sign * operand
sign = 1
operand = 0
elif ch == '-':
res += sign * operand
sign = -1
operand = 0
elif ch == '(':
stack.append(res)
stack.append(sign)
sign = 1
res = 0
elif ch == ')':
res += sign * operand
res *= stack.pop()
res += stack.pop()
operand = 0
return res + sign * operand
(278)227 Basic Calculator II(Medium)
实现基本计算器来评估简单的表达式字符串。 表达式字符串仅包含非负整数,+, – ,*,/运算符和空格。整数除法应截断为零。

思路:
使用stack的思想,末尾加0,是因为担心末尾是数字加全
为了防止负号向下取整的情况,所以不用//(只能适用于python3)
最后sum一下
def calculate(self, s: str) -> int:
#防止最后有数字,没有加上
s += '+0'
stack, num, preop = [], 0, '+'
for i in range(len(s)):
if s[i].isdigit():
num = num * 10 + int(s[i])
elif s[i] != ' ':
if preop == '-':
stack.append(-num)
elif preop == '+':
stack.append(num)
elif preop == '*':
stack.append(stack.pop() * num)
else:
#为了防止负号向下取整的情况,所以不用//(只能适用于python3)
stack.append(int(stack.pop() / num ))
preop, num = s[i], 0
return sum(stack)
(279)84. Largest Rectangle in Histogram***(Hard)
给定n个非负整数表示直方图的条形高度,其中每个条形的宽度为1,找到直方图中最大矩形的区域。
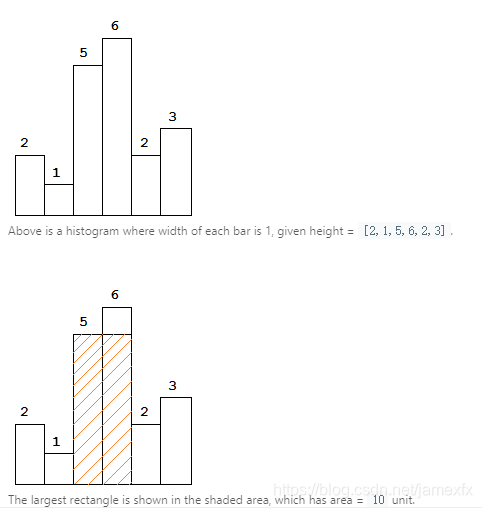
思路:题型和11题类似,但是解法不同。
此题用stack的思想O(n),重要的几个trick
1、stack = [-1] height.append(0) #在最后面添加一个最小数
2、循环当矩阵不是递增的时候,弹出末尾的元素,然后算面积。否则stack.append(i)(注:是加入索引)
用栈来模拟,遍历heights数组,如果大于栈顶元素,就push进去;否则,持续弹栈来计算从栈顶点到降序点的矩阵大小。然后将这一部分全部替换为降序点的值,即做到了整体依然是有序非降的。
整个过程中,即把所有的局部最大矩阵计算过了,又在宽度范围内保留了全部的场景。
举例,2,1,5,6,3的场景。
先加入一个0,方便最后可以全部弹栈出来。变成:2,1,5,6,3,0.
2进栈,1比栈顶小,对2进行出栈,area = 2;
5,6都是非降的,继续进栈,栈为1,5,6;
遇到3,是一个降序点;开始弹栈,6出栈,对应area=61; 5出栈对应area=52;下一个1比3小,不需要弹栈。然后将5、6的弹栈后的空位压栈为3,这是栈为1,1,3,3,3;
下一步遇到0,开始依次出栈,得到area=31,32,33,14,1*5。
遍历结束。整个过程中max的area为10.
def largestRectangleArea(self, height):
#在最后面添加一个最小数
height.append(0)
stack = [-1]
ans = 0
for i in range(len(height)):
while height[i]<height[stack[-1]]:
h = height[stack.pop()]
w = i - stack[-1] -1
ans = max(ans,h*w)
print(ans)
stack.append(i)
return ans
(280)215 Kth Largest Element in an Array(Medium)
使用归并+非递归O(n)
class Solution(object):
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
pos = len(nums)+1 -k
start = 0
end = len(nums)-1
while True:
i,j = self.partition(nums,start,end,k)
if i+1-start>=pos:
end = i
elif j-start>=pos:
return nums[j-1]
else:
pos -=(j-start)
start = j
def partition(self,nums,start,end,pos):
pivot = nums[(start+end)//2]
i = start -1
j = end + 1
k = start
while k<j:
if nums[k]<pivot:
i+=1
nums[k],nums[i] = nums[i],nums[k]
elif nums[k]>pivot:
j -=1
nums[k],nums[j] = nums[j],nums[k]
k -=1
k +=1
return i,j
(281)347 Top K Frequent Elements(Medium)
给定非空的整数数组,返回k个最常见的元素。
您可以假设k始终有效,1≤k≤唯一元素的数量。 算法的时间复杂度必须优于O(n log n),其中n是数组的大小。
思路:
1、首先统计每个词出现的次数,同时计算最大的次数是多少
2、然后使用空间换空间,将次数作为键,元素作为值
3、然后从后往前遍历,遍历每个元素中的值,然后每次加入的时候判断一下是否长度为k了
def topKFrequent(nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
dict = {}
max_len = 1
for num in nums:
if num in dict:
dict[num] += 1
max_len = max(dict[num], max_len)
else:
dict[num] = 1
bucket = [[] for _ in range(max_len + 1)]
for key, val in dict.items():
bucket[val].append(key)
ret = []
for row in reversed(bucket):
if not row:
continue
else:
for i in range(len(row)):
ret.append(row[i])
if len(ret) == k:
return ret
(282)218 The Skyline Problem(Hard)(不会)
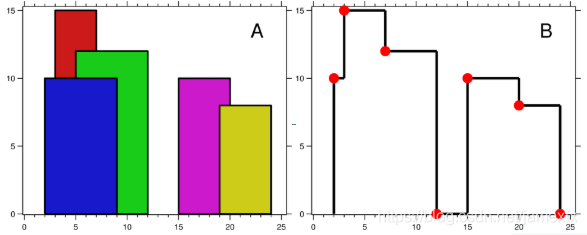
城市的天际线是从远处观看时该城市所有建筑物形成的轮廓的外部轮廓。现在假设您获得了所有建筑物的位置和高度,如城市景观照片所示(图A),编写程序以输出这些建筑物共同形成的天际线(图B)。
每个建筑物的几何信息由整数三元组[Li,Ri,Hi]表示,其中Li和Ri分别是第i个建筑物左右边缘的x坐标,Hi是其高度。保证0≤Li,Ri≤INT_MAX,0 <Hi≤INT_MAX,Ri-Li> 0.您可以假设所有建筑物都是在高度为0的绝对平坦表面上接地的完美矩形。
例如,图A中所有建筑物的尺寸记录为:[[2 9 10],[3 7 15],[5 12 12],[15 20 10],[19 24 8]]
输出是[关键点]列表(图B中的红点),格式为[[x1,y1],[x2,y2],[x3,y3],…],它们唯一地定义了天际线。
关键点是水平线段的左端点。请注意,最右边建筑物结束的最后一个关键点仅用于标记天际线的终止,并且始终没有高度。
此外,任何两个相邻建筑物之间的地面应被视为天际线轮廓的一部分。
例如,图B中的天际线应表示为:[[2 10],[3 15],[7 12],[12 0],[15 10],[20 8],[24,0]] 。
输出列表必须按x位置排序。
这里必须没有输出天际线中相同高度的连续水平线。例如,[… [2 3],[4 5],[7 5],[11 5],[12 7] …]是不可接受的;高度为5的三条线应该在最终输出中合并为一条:[…[2 3], [4 5], [12 7], …]
class Solution:
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
# 对于一个 building, 他由 (l, r, h) 三元组组成, 我们可以将其分解为两种事件:
# 1. 在 left position, 高度从 0 增加到 h(并且这个高度将持续到 right position);
# 2. 在 right position, 高度从 h 降低到 0.
# 由此引出了 event 的结构: 在某一个 position p, 它引入了一个高度为 h 的 skyline, 将一直持续到另一 end postion
# 对于在 right position 高度降为 0 的 event, 它的持续长度时无效的
# 只保留一个 right position event, 就可以同时触发不同的两个 building 在同一 right position 从各自的 h 降为 0 的 event, 所以对 right position events 做集合操作会减少计算量
# 由于需要从左到右触发 event, 所以按 postion 对 events 进行排序
# 并且, 对于同一 positon, 我们需要先触发更高 h 的事件, 先触发更高 h 的事件后, 那么高的 h 相比于低的 h 会占据更高的 skyline, 低 h 的 `key point` 就一定不会产生; 相反, 可能会从低到高连续产生冗余的 `key point`
# 所以, event 不仅需要按第一个元素 position 排序, 在 position 相同时, 第二个元素 h 也是必须有序的
events = sorted([(l, -h, r) for l, r, h in buildings] + list({(r, 0, 0) for l, r, h in buildings}))
# res 记录了 `key point` 的结果: [x, h]
# 同时 res[-1] 处的 `key point` 代表了在下一个 event 触发之前, 一直保持的最高的 skyline
# hp 记录了对于一条高为 h 的 skyline, 他将持续到什么 position 才结束: [h, endposition]
# 在同时有多条 skyline 的时候, h 最高的那条 skyline 会掩盖 h 低的 skyline, 因此在 event 触发时, 需要得到当前最高的 skyline
# 所以利用 heap 结构存储 hp, 它的第一个值永远为列表中的最小值: 因此在 event 中记录的是 -h, heap 结构就会返回最高的 skyline. 同时, h 必须在 endposition 之前, 因为它按第一个元素排序
res, hp = [[0, 0]], [(0, float('inf'))]
for l, neg_h, r in events:
# 触发 event 时, 首先要做的就是清除已经到 endposition 的 skyline
# hp: [h, endposition]
# 如果当前 position 大于等于了 hp 中的 endposition, 那么该 skyline 会被清除掉
# 由于在有 high skyline 的情况下, low skyline 不会有影响, 因此, 只需要按从高到低的方式清除 skyline, 直到剩下一个最高的 skyline 并且它的 endposition 大于当前 position
while l >= hp[0][1]:
heapq.heappop(hp)
# 对于高度增加到 h 的时间(neg_h < 0), 我们需要添加一个 skyline, 他将持续到 r 即 endposition
if neg_h:
heapq.heappush(hp, (neg_h, r))
# 由于 res[-1][1] 记录了在当前事件触发之前一直保持的 skyline
# 如果当前事件触发后 skyline 发生了改变
# 1. 来了一条新的高度大于 h 的 skyline
# 2. res[-1] 中记录的 skyline 到达了 endposition
# 这两种事件都会导致刚才持续的 skyline 与现在最高的 skyline 不同; 同时, `key point` 产生了, 他将被记录在 res 中
if res[-1][1] != -hp[0][0]:
res.append([l, -hp[0][0]])
return res[1:]
(283)332 Reconstruct Itinerary(Medium)
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 出发。
说明:
如果存在多种有效的行程,你可以按字符自然排序返回最小的行程组合。例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前
所有的机场都用三个大写字母表示(机场代码)。
假定所有机票至少存在一种合理的行程。
341 Flatten Nested List Iterator(Medium)(未写)
Bit Manipulation
(284)389 Find the Difference(Easy)
给定两个字符串s和t,它们只包含小写字母。 字符串t由随机混洗字符串s生成,然后在随机位置再添加一个字母。 找到t中添加的字母。
思路:
def findTheDifference(self, s, t):
"""
:type s: str
:type t: str
:rtype: str
"""
res = ord(t[-1])
for i in range(len(s)):
res =res+ ord(t[i]) -ord(s[i])
return chr(res)
(285)136. Single Number(Easy)
给定一个非空的整数数组,除了一个元素外,每个元素都会出现两次。找一个单一的。 注意: 您的算法应具有线性运行时复杂性。你能不用额外的内存来实现吗?

思路:
使用异或操作
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
a=0
for i in nums:
a = a^i
print(a)
return a
318. Maximum Product of Word Lengths(Medium)(未写)
Topological Sort
(286)207. Course Schedule(Medium)
您必须参加总共n门课程,标记为0到n-1。 有些课程可能有先决条件,例如,要修课程0,你必须先修课程1,表示为一对:[0,1]
鉴于课程总数和先决条件对列表,您是否可以完成所有课程?
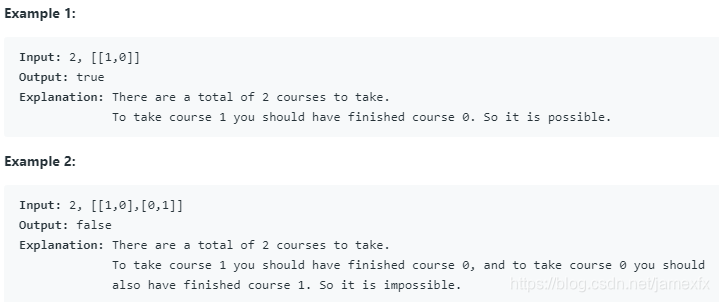
思路:
此题考验的是无环有向图,还有拓扑排序
1、首先根据所有课程的先决条件构建无环有向图
2、存储所有节点的入度
3、当入度为0时,加入pre中,然后使用循环把所有和pre中有关的节点入度都减一
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
graph = [[] for _ in range(numCourses)]
degree = [0 for i in range(numCourses)]
for i in prerequisites:
graph[i[0]].append(i[1])
degree[i[1]] +=1
pre = []
for i in range(len(degree)):
if degree[i] ==0:
pre.append(i)
while(pre):
node = pre.pop()
for i in graph[node]:
degree[i] -=1
if degree[i] == 0:
pre.append(i)
return max(degree)==0
(287)210. Course Schedule II(Medium)
您必须参加总共n门课程,标记为0到n-1。 有些课程可能有先决条件,例如,要修课程0,你必须先修课程1,表示为一对:[0,1]
鉴于课程总数和先决条件对列表,列出按顺序上的课程
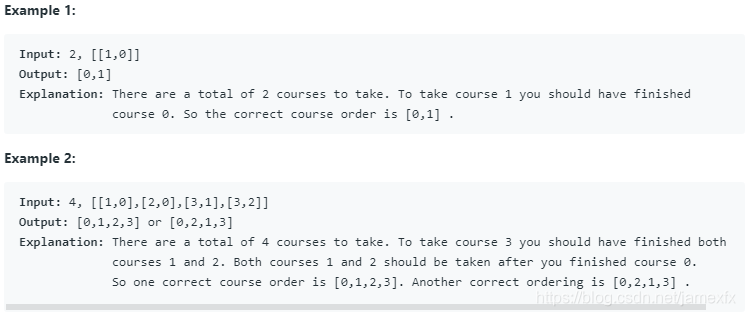
思路:(和207类似)
此题考验的是无环有向图,还有拓扑排序
1、首先根据所有课程的先决条件构建无环有向图
2、存储所有节点的入度
3、当入度为0时,加入pre中,然后使用循环把所有和pre中有关的节点入度都减一,使用一个a节点记录所有节点为0的节点
def findOrder(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: List[int]
"""
graph = [[] for _ in range(numCourses)]
degree = [0 for i in range(numCourses)]
for i in prerequisites:
graph[i[1]].append(i[0])
degree[i[0]] +=1
pre = []
a = []
for i in range(len(degree)):
if degree[i] ==0:
pre.append(i)
a.append(i)
while(pre):
node = pre.pop()
for i in graph[node]:
degree[i] -=1
if degree[i] == 0:
pre.append(i)
a.append(i)
return a if len(a)==numCourses else []
269 Alien Dictionary(Hard)(未写)
Random
384 Shuffle an Array
398 Random Pick Index
382 Linked List Random Node
380 Insert Delete GetRandom O(1)
381 Insert Delete GetRandom O(1) – Duplicates allowed
(288)138. Copy List with Random Pointer(Medium)
复制一个复杂链表,这个复杂链表是指出了值和next指针外,还有一个random指针可能指向任何位置的链表节点或空。

思路:
1、使用字典来创建类型,记得要添加一个dict[None] = None 类型
2、然后next遍历,赋值
def copyRandomList(self, head):
"""
:type head: Node
:rtype: Node
"""
dict = collections.defaultdict(lambda:Node(0,0,0))
dict[None] = None
n = head
while n:
dict[n].val = n.val
dict[n].next = dict[n.next]
dict[n].random = dict[n.random]
n = n.next
return dict[head]
Graph
(289)133. Clone Graph(Medium)
给定连接的无向图中的节点的引用,返回图的深拷贝(克隆)。图中的每个节点都包含其邻居的val(int)和列表(List [Node])。

思路:
1、使用DFS遍历整个网络
2、如果存在该节点,则直接返回该节点的指针
3、不存在则创建Node,然后遍历其neighbors
def cloneGraph(self, node):
"""
:type node: Node
:rtype: Node
"""
if node == None:
return None
d = {}
def dfs(node):
if node in d:
return d[node]
ans = Node(node.val,[])
d[node] = ans
for i in node.neighbors:
ans.neighbors.append(dfs(i))
return ans
return dfs(node)
399 Evaluate Division
310 Minimum Height Tree
(290)149. Max Points on a Line(Hard)(很少考)
给定2D平面上的n个点,找到位于同一直线上的最大点数。

思路:
首先他们满足在同一直线上,即a = (x1-x0)/(y1 – y0) = (x2-x1)/(y2-y1)
1、使用双层循环进行判断,定义一个全局变量m来存储当前最大
2、首先判断两个点是不是重叠,是的话,same+1
3、定义一个字典,用来存储不同a对应的数量,找出最大
from fractions import Fraction
class Solution(object):
def maxPoints(self, points):
"""
:type points: List[List[int]]
:rtype: int
"""
m = 0
for i in range(len(points)):
if m>=len(points)-i:
break
dict = {'i':1}
same = 0
for j in range(i+1,len(points)):
if points[i][0] ==points[j][0] and points[j][1]==points[i][1]:
same +=1
continue
if points[i][0] == points[j][0]:
slop = i
else:
slop = Fraction((points[j][1]-points[i][1]),(points[j][0] - points[i][0]))
if slop not in dict:
dict[slop] = 1
dict[slop] +=1
m = max(m,max(dict.values())+same)
return m
Union FInd
261 Graph Valid Tree
323 Number of Connected Components in an Undirected Graph
305 Number of Islands II
Trie
(291)208. Implement Trie (Prefix Tree)(Medium)
使用insert,search和startsWith方法实现trie。

思路:
定义一个TrieNode,包含word(判断这个word是不是在trie中)、children存储这个字的每个字符
class TrieNode:
def __init__(self):
self.word = False
self.children = {}
class Trie(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = TrieNode()
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: None
"""
node = self.root
for i in word:
if i not in node.children:
node.children[i] = TrieNode()
node = node.children[i]
node.word = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
node = self.root
for i in word:
if i not in node.children:
return False
node = node.children[i]
return node.word
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
node = self.root
for i in prefix:
if i not in node.children:
return False
node = node.children[i]
return True
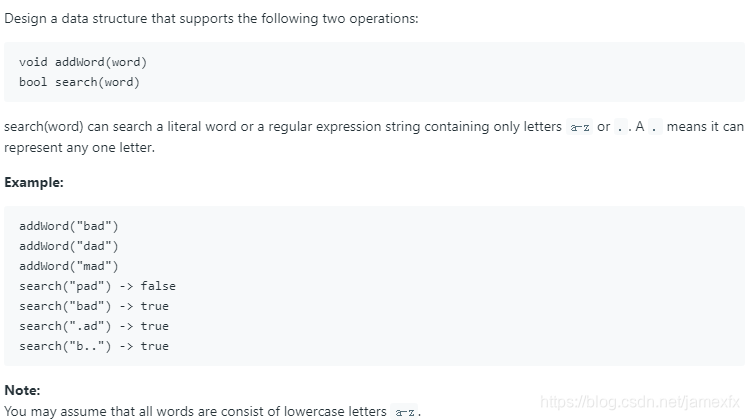
(292)211. Add and Search Word – Data structure design(Medium)
思路:
1、初始化使用list dict
2、通过字的长度进行存储 word
3、使用双循环判断word在哪个里面
class WordDictionary(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.word_dict = collections.defaultdict(list)
def addWord(self, word):
"""
Adds a word into the data structure.
:type word: str
:rtype: None
"""
if word:
self.word_dict[len(word)].append(word)
def search(self, word):
"""
Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
:type word: str
:rtype: bool
"""
if not word:
return False
if '.' not in word:
return word in self.word_dict[len(word)]
for v in self.word_dict[len(word)]:
success = True
for i,char in enumerate(word):
if char!=v[i] and char!='.':
success = False
break
return success
# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)
(293)212. Word Search II(Hard)
给定2D板和字典中的单词列表,找到板中的所有单词。
每个字必须由顺序相邻的单元的字母构成,其中“相邻”单元是水平或垂直相邻的单元。一个单词中不能多次使用相同的字母单元格。

思路:
1、使用字典树Trie,把所有要找的单词放在字典树里,然后每个元素上下左右搜索,找到了就结束当前分支的搜索
class TrieNode():
def __init__(self):
self.children = collections.defaultdict(TrieNode)
self.isWord = False
class Trie():
def __init__(self):
self.root = TrieNode()
def insert(self,word):
node = self.root
for w in word:
if w not in node.children:
node.children[w] = TrieNode()
node = node.children[w]
node.isWord = True
def search(self,word):
node = self.root
for w in word:
node = node.children.get(w)
if not node:
return False
return node.isWord
class Solution(object):
def findWords(self, board, words):
"""
:type board: List[List[str]]
:type words: List[str]
:rtype: List[str]
"""
res = []
trie = Trie()
node = trie.root
for w in words:
trie.insert(w)
for i in range(len(board)):
for j in range(len(board[0])):
self.dfs(board,node,i,j,'',res)
return res
def dfs(self,board,node,i,j,path,res):
if node.isWord:
res.append(path)
node.isWord = False
if i<0 or i>=len(board) or j<0 or j>=len(board[0]):
return
temp = board[i][j]
node = node.children.get(temp)
if not node:
return
board[i][j] = '#'
self.dfs(board,node,i+1,j,path+temp,res)
self.dfs(board,node,i,j+1,path+temp,res)
self.dfs(board,node,i-1,j,path+temp,res)
self.dfs(board,node,i,j-1,path+temp,res)
board[i][j] = temp
Design
359 Logger Rate Limiter
346 Moving Average from Data Stream (Sliding Window)
362 Design Hit Counter
281 Zigzag Iterator
284 Peeking Iterator
251 Flatten 2D Vector
288 Unique Word Abbreviation
170 Two Sum III – Data structure design
348 Design Tic-Tac-Toe
379 Design Phone Directory
353 Design Snake Game
(294)146. LRU Cache(Hard)
设计并实现最近最少使用(LRU)缓存的数据结构。它应该支持以下操作:get和put。
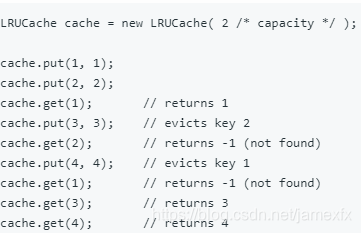
get(key) – Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
put(key, value) – Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.
思路:
由于要求时间复杂度为O(1),定义一个双向链表(自带一个头结点和尾结点)
1、init() 包括capacity、字典、头尾结点
2、get()判断是否在字典、然后移除该结点,再加入该结点(保证在末尾)
3、set()判断是否包含关键词,如果有,删除并更改。如果容量不够,删掉最后一个。字典也要记得删
4、定义node结点和remove函数和add函数
class Node(object):
def __init__(self,key,value):
self.key = key
self.value = value
self.next = None
self.pre = None
class LRUCache(object):
def __init__(self, capacity):
"""
:type capacity: int
"""
self.capacity = capacity
self.dict = {}
self.head = Node(0,0)
self.tail = Node(0,0)
self.head.next = self.tail
self.tail.pre = self.head
def get(self, key):
"""
:type key: int
:rtype: int
"""
if key in self.dict:
self.remove(self.dict[key])
self.add(self.dict[key])
return self.dict[key].value
return -1
def put(self, key, value):
"""
:type key: int
:type value: int
:rtype: None
"""
if key in self.dict:
self.remove(self.dict[key])
n = Node(key,value)
self.dict[key] = n
self.add(n)
if len(self.dict)>self.capacity:
r = self.head.next
self.remove(r)
del self.dict[r.key]
def remove(self,node):
next = node.next
next.pre = node.pre
node.pre.next = next
def add(self,node):
pre = self.tail.pre
pre.next = node
node.next = self.tail
node.pre = pre
self.tail.pre = node
355 Design Twitter
303 Range Sum Query – Immutable
304 Range Sum Query 2D – Immutable
307 Range Sum Query – Mutable Binary Index Tree
308 Range Sum Query 2D – Mutable Binary Index Tree
面经面试题
(295)抖音红人(字节跳动)
思路:
1、首先将第一层关系使用set字典形式存储
2、间接关系使用三层循环,第一层循环人数,第二层循环字典,第三层循环字典内的元素
3、需要元素量等于总人数的,加一
import collections
class solution:
def split_star(list,nums):
if len(list) ==0:
return 0
res = collections.defaultdict(set)
for i,v in enumerate(list):
# 奇数表示拿到的是关注的对象 奇数前面的偶数表示关注此对象的人
if i%2:
res[v].add(v)
res[v].add(list[i-1])
# 需要多次检测,因为有间接的关注关系
for i in range(nums):
# star 表示被关注的人, user表示关注者
for star,user in res.items():
add_people = set()
for u in user:
if u in res:
add_people |= res[u]
res[star] |= add_people
star_num = 0
for star,user in res.items():
if len(user) == nums:
star_num +=1
return star_num
if __name__ =='__main__':
N = int(input())
list = list(map(int,input().split()))
print(solution.split_star(list,N))
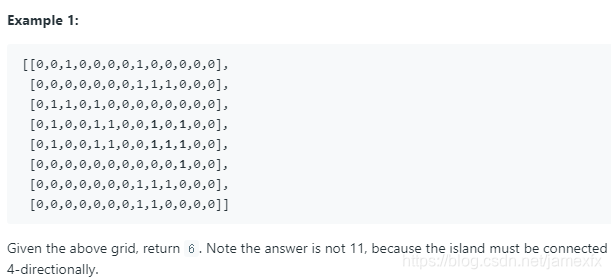
(296)695. Max Area of Island(Medium)(字节跳动)
给定0和1的非空二维阵列网格,岛是一组1(表示陆地)4方向连接(水平或垂直)。您可以假设网格的所有四个边缘都被水包围。 找到给定2D阵列中岛的最大面积。 (如果没有岛,则最大面积为0.)
思路:
这个最大区域(不是面积)是指连接1的最大范围,有就加一。
使用dfs进行遍历
首先循环整个表格,然后如果该区域是1,则使用dfs进行遍历,遍历之前需要把当前节点设为2,防止再次访问
def maxAreaOfIsland(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
def dfs(i,j):
if 0<=i<len(grid) and 0<=j<len(grid[0]) and grid[i][j] == 1:
grid[i][j] = 'X'
ans = 1
for i in map(dfs,(i+1,i-1,i,i),(j,j,j+1,j-1)):
ans += i
return ans
return 0
res = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
res = max(res,dfs(i,j))
return res
(297)max_Tree(快手)
给出一个没有重复的整数数组,在此数组上建立最大树的定义如下:
1.根是数组中最大的数
2.左子树和右子树元素分别是被父节点元素切分开的
子数组中的最大值
利用给定的数组构造最大树。

class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
def maxTree(A):
# write your code here
stack = []
for element in A:
node = TreeNode(element)
while len(stack) != 0 and element > stack[-1].val:
node.left = stack.pop()
if len(stack) != 0:
stack[-1].right = node
stack.append(node)
return stack[0]
print(maxTree( [3, 5, 6, 0, 2, 1]))
十大排序
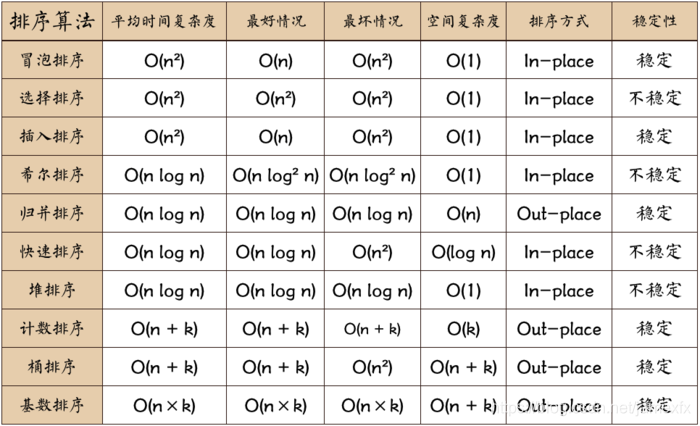
In-place:占用常数内存,不占用额外内存
Out-place:占用额外内存
n:数据规模
k:“桶”的个数
稳定性:排序后2个相等键值的顺序和排序之前它们的顺序相同
(298)冒泡排序
冒泡排序每次找出一个最大的元素,因此需要遍历 n-1 次。
def bubbleSort(nums):
for i in range(len(nums) - 1): # 遍历 len(nums)-1 次
for j in range(len(nums) - i - 1): # 已排好序的部分不用再次遍历
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j] # Python 交换两个数不用中间变量
return nums
(299)选择排序
选择排序不受输入数据的影响,即在任何情况下时间复杂度不变。选择排序每次选出最小的元素,因此需要遍历 n-1 次。
def selectionSort(nums):
for i in range(len(nums) - 1): # 遍历 len(nums)-1 次
minIndex = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[minIndex]: # 更新最小值索引
minIndex = j
nums[i], nums[minIndex] = nums[minIndex], nums[i] # 把最小数交换到前面
return nums
(300)插入排序
插入排序如同打扑克一样,每次将后面的牌插到前面已经排好序的牌中。插入排序有一种优化算法,叫做拆半插入。因为前面是局部排好的序列,因此可以用折半查找的方法将牌插入到正确的位置,而不是从后往前一一比对。折半查找只是减少了比较次数,但是元素的移动次数不变,所以时间复杂度仍为 O(n^2) !
def insertionSort(nums):
for i in range(len(nums) - 1): # 遍历 len(nums)-1 次
curNum, preIndex = nums[i+1], i # curNum 保存当前待插入的数
while preIndex >= 0 and curNum < nums[preIndex]: # 将比 curNum 大的元素向后移动
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
nums[preIndex + 1] = curNum # 待插入的数的正确位置
return nums
(301)希尔排序
希尔排序是插入排序的一种更高效率的实现。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
【例子】对于待排序列 {44,12,59,36,62,43,94,7,35,52,85},我们可设定增量序列为 {5,3,1}。
【解析】第一个增量为 5,因此 {44,43,85}、{12,94}、{59,7}、{36,35}、{62,52} 分别隶属于同一个子序列,子序列内部进行插入排序;然后选取第二个增量3,因此 {43,35,94,62}、{12,52,59,85}、{7,44,36} 分别隶属于同一个子序列;最后一个增量为 1,这一次排序相当于简单插入排序,但是经过前两次排序,序列已经基本有序,因此此次排序时间效率就提高了很多。希尔排序过程如下:

def shellSort(nums):
lens = len(nums)
gap = 1
while gap < lens // 3:
gap = gap * 3 + 1 # 动态定义间隔序列
while gap > 0:
for i in range(gap, lens):
curNum, preIndex = nums[i], i - gap # curNum 保存当前待插入的数
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + gap] = nums[preIndex] # 将比 curNum 大的元素向后移动
preIndex -= gap
nums[preIndex + gap] = curNum # 待插入的数的正确位置
gap //= 3 # 下一个动态间隔
return nums
(302)归并排序
归并排序须知:
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第2种方法)
- 自下而上的迭代
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
递归
def mergeSort(nums):
# 归并过程
def merge(left, right):
result = [] # 保存归并后的结果
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result = result + left[i:] + right[j:] # 剩余的元素直接添加到末尾
return result
# 递归过程
if len(nums) <= 1:
return nums
mid = len(nums) // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
return merge(left, right)
非递归
#low = low +2*i #middle = low +i #high = min(low+2*i,len(seq))
def merge_sort(seq):
i = 1 # i是步长
while i < len(seq):
low = 0
while low < len(seq):
mid = low + i #mid前后均为有序
high = min(low+2*i,len(seq))
if mid < high:
merge(seq, low, mid, high)
low += 2*i
i *= 2
def merge(seq, low, mid, high):
比上一步多了一个mid,其它一样
原地归并排序
都是划分子序列然后合并子序列,但是在实现合并子序列的时候使用了手摇算法实现了序列的合并,可以做到O(1)的辅助空间。但是理论上合并长度n和m的子序列最坏的复杂度为2
n
m,所以原地归并排序实际意义并不大。
手摇算法
假如要将序列1 2 3 4 5的4 5提到1 2 3前面
-> 1 2 3 4 5 原数组
-> 3 2 1 5 4 O(n)的时间将1 2 3翻转,4 5翻转
-> 4 5 1 2 3 O(n)的时间再将数组翻转一次
这时候我们可以看到4 5已经在1 2 3的前面了。我们可以清楚地看到每个数都被交换了2次,所以手摇算法的时间复杂度是2*(n+m)

## O(1)空间复杂度的归并排序
## 反转列表
def reverveList(nums,l,r):
while l<r:
nums[l],nums[r] = nums[r],nums[l]
l +=1
r -=1
## 手摇算法
def head_shake(nums,l,m,r):
reverveList(nums,l,m-1)
reverveList(nums,m,r-1)
reverveList(nums,l,r-1)
## O(1)空间复杂度的归并排序(使用手摇算法)
def merge(nums,low,mid,high):
while low<mid and mid<high:
while low<mid and nums[low]<=nums[mid]:
low +=1
moved = 0
while mid<high and nums[low]>nums[mid]:
mid +=1
moved +=1
head_shake(nums,low,mid-moved,mid)
low += moved
## 非递归方式
def mergeSort(nums):
i = 1
while i<len(nums):
low =0
while low<len(nums):
mid = low +i
high = min(low+2*i,len(nums))
if mid<high:
merge(nums,low,mid,high)
low +=2*i
i *=2
return nums
print(mergeSort([6,5,4,3,2,1]))
(303)快速排序
又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。它是处理大数据最快的排序算法之一,虽然 Worst Case 的时间复杂度达到了 O(n²),但是在大多数情况下都比平均时间复杂度为 O(n log n) 的排序算法表现要更好,因为 O(n log n) 记号中隐含的常数因子很小,而且快速排序的内循环比大多数排序算法都要短小,这意味着它无论是在理论上还是在实际中都要更快,比复杂度稳定等于 O(n log n) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。它的主要缺点是非常脆弱,在实现时要非常小心才能避免低劣的性能。
def quickSort(nums): # 这种写法的平均空间复杂度为 O(nlogn)
if len(nums) <= 1:
return nums
pivot = nums[0] # 基准值
left = [nums[i] for i in range(1, len(nums)) if nums[i] < pivot]
right = [nums[i] for i in range(1, len(nums)) if nums[i] >= pivot]
return quickSort(left) + [pivot] + quickSort(right)
'''
@param nums: 待排序数组
@param left: 数组上界
@param right: 数组下界
'''
def quickSort2(nums, left, right): # 这种写法的平均空间复杂度为 O(logn)
# 分区操作
def partition(nums, left, right):
pivot = nums[left] # 基准值
while left < right:
while left < right and nums[right] >= pivot:
right -= 1
nums[left] = nums[right] # 比基准小的交换到前面
while left < right and nums[left] <= pivot:
left += 1
nums[right] = nums[left] # 比基准大交换到后面
nums[left] = pivot # 基准值的正确位置,也可以为 nums[right] = pivot
return left # 返回基准值的索引,也可以为 return right
# 递归操作
if left < right:
pivotIndex = partition(nums, left, right)
quickSort2(nums, left, pivotIndex - 1) # 左序列
quickSort2(nums, pivotIndex + 1, right) # 右序列
return nums
(304)堆排序
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大根堆:每个节点的值都大于或等于其子节点的值,用于升序排列;
- 小根堆:每个节点的值都小于或等于其子节点的值,用于降序排列。
如下图所示,首先将一个无序的序列生成一个最大堆,如图(a)所示。接下来我们不需要将堆顶元素输出,只要将它与堆的最后一个元素对换位置即可,如图(b)所示。这时我们确知最后一个元素 99 一定是递增序列的最后一个元素,而且已经在正确的位置上。 现在问题变成了如何将剩余的元素重新生成一个最大堆——也很简单,只要依次自上而下进行过滤,使其符合最大堆的性质。图(c)是调整后形成的新的最大堆。要注意的是,99 已经被排除在最大堆之外,即在调整的时候,堆中元素的个数应该减 1 。结束第 1 轮调整后,再次将当前堆中的最后一个元素 22 与堆顶元素换位,如图(d)所示,再继续调整成新的最大堆……如此循环,直到堆中只剩 1 个元素,即可停止,得到一个从小到大排列的有序序列。
构建二叉堆的算法复杂度是O(N)。然后每次下滤的算法复杂度是O(logN),一共下滤K次,算法复杂度是O(N+K*logN)。
# 大根堆(从小打大排列)
def heapSort(k,nums):
# 调整堆
def adjustHeap(nums, i, size):
# 非叶子结点的左右两个孩子
lchild = 2 * i + 1
rchild = 2 * i + 2
# 在当前结点、左孩子、右孩子中找到最大元素的索引
largest = i
if lchild < size and nums[lchild] > nums[largest]:
largest = lchild
if rchild < size and nums[rchild] > nums[largest]:
largest = rchild
# 如果最大元素的索引不是当前结点,把大的结点交换到上面,继续调整堆
if largest != i:
nums[largest], nums[i] = nums[i], nums[largest]
# 第 2 个参数传入 largest 的索引是交换前大数字对应的索引
# 交换后该索引对应的是小数字,应该把该小数字向下调整
adjustHeap(nums, largest, size)
# 建立堆
def builtHeap(nums, size):
for i in range(len(nums)//2)[::-1]: # 从倒数第一个非叶子结点开始建立大根堆
adjustHeap(nums, i, size) # 对所有非叶子结点进行堆的调整
# print(nums) # 第一次建立好的大根堆
# 堆排序
size = len(nums)
if k>size:
k = size
builtHeap(nums, size)
for i in range(len(nums)-k,len(nums))[::-1]:
# 每次根结点都是最大的数,最大数放到后面
nums[0], nums[i] = nums[i], nums[0]
# 交换完后还需要继续调整堆,只需调整根节点,此时数组的 size 不包括已经排序好的数
adjustHeap(nums, 0, i)
return nums[len(nums)-k:] # 由于每次大的都会放到后面,因此最后的 nums 是从小到大排列
print(heapSort(6,[5,11,7,4,3,17,20]))
(305)计数排序
计数排序要求输入数据的范围在 [0,N-1] 之间,则可以开辟一个大小为 N 的数组空间,将输入的数据值转化为键存储在该数组空间中,数组中的元素为该元素出现的个数。它是一种线性时间复杂度的排序。
def countingSort(nums):
bucket = [0] * (max(nums) + 1) # 桶的个数
for num in nums: # 将元素值作为键值存储在桶中,记录其出现的次数
bucket[num] += 1
i = 0 # nums 的索引
for j in range(len(bucket)):
while bucket[j] > 0:
nums[i] = j
bucket[j] -= 1
i += 1
return nums
(306)桶排序
桶排序须知:
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
什么时候最快(Best Cases):
当输入的数据可以均匀的分配到每一个桶中
什么时候最慢(Worst Cases):
当输入的数据被分配到了同一个桶中
def bucketSort(nums, defaultBucketSize = 5):
maxVal, minVal = max(nums), min(nums)
bucketSize = defaultBucketSize # 如果没有指定桶的大小,则默认为5
bucketCount = (maxVal - minVal) // bucketSize + 1 # 数据分为 bucketCount 组
buckets = [] # 二维桶
for i in range(bucketCount):
buckets.append([])
# 利用函数映射将各个数据放入对应的桶中
for num in nums:
buckets[(num - minVal) // bucketSize].append(num)
nums.clear() # 清空 nums
# 对每一个二维桶中的元素进行排序
for bucket in buckets:
insertionSort(bucket) # 假设使用插入排序
nums.extend(bucket) # 将排序好的桶依次放入到 nums 中
return nums
(307)基数排序
基数排序是桶排序的一种推广,它所考虑的待排记录包含不止一个关键字。例如对一副牌的整理,可将每张牌看作一个记录,包含两个关键字:花色、面值。一般我们可以将一个有序列是先按花色划分为四大块,每一块中又再按面值大小排序。这时“花色”就是一张牌的“最主位关键字”,而“面值”是“最次位关键字”。
基数排序有两种方法:
MSD (主位优先法):从高位开始进行排序
LSD (次位优先法):从低位开始进行排序
# LSD Radix Sort
def radixSort(nums):
mod = 10
div = 1
mostBit = len(str(max(nums))) # 最大数的位数决定了外循环多少次
buckets = [[] for row in range(mod)] # 构造 mod 个空桶
while mostBit:
for num in nums: # 将数据放入对应的桶中
buckets[num // div % mod].append(num)
i = 0 # nums 的索引
for bucket in buckets: # 将数据收集起来
while bucket:
nums[i] = bucket.pop(0) # 依次取出
i += 1
div *= 10
mostBit -= 1
return nums
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶
计数排序:每个桶只存储单一键值
桶排序:每个桶存储一定范围的数值
哪些排序算法可以在未结束排序时找出第 k 大元素?
冒泡、选择、堆排序、快排(想想为什么?)
快排、归并排序、堆排序、计数排序(桶排序)一般是面试中常问的题目,其中比较难的是堆排序,因为涉及建堆、调整堆的过程,手写该算法还是有一定难度的。