RNN,LSTM,GRU回顾（主要知道代码怎么使用）

RNN的计算流程

RNN的计算流程图如下图所示：↓

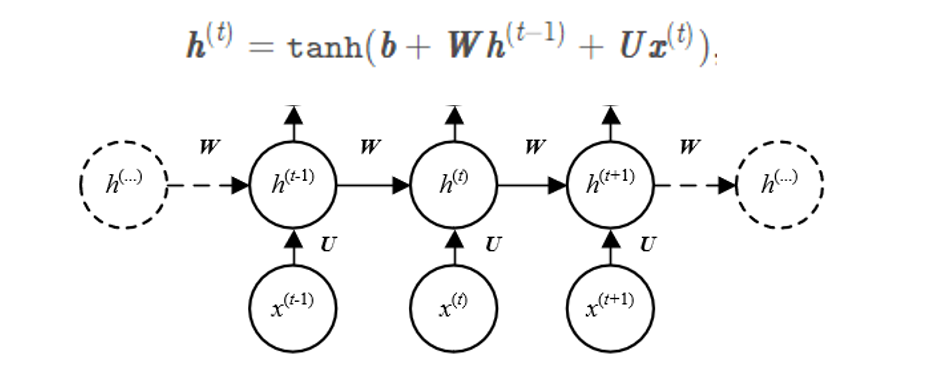
在这里插入图片描述

nn.RNN的初始化是这样规定的：↓

rnn = nn.RNN(input_size, hidden_size, bias=False, batch_first=True)

这里的
input_size
就是其中一个

x^t

$x^{t}$

的维度大小，

x^t

$x^{t}$

是一个一维的tensor。RNN的初始化不需要去关心

x^t

$x^{t}$

的数量是多少（这里的数量也就是一个句子的长度是多少），也不需要关心batch是多少
（这里的batch也就是句子的数量有多少，不关心batch是多少是所有神经网络网路接口的共性，比如cv中的CNN的初始化，也只需要知道图像的深度，需要映射到的深度等即可，不关心有多少张图像，因为神经网络接口会自动做批量处理，即会用该网路接口的对象，对所有图像同时做相同的操作）

而里面的
hidden_size
，也就是图中

h^t

$h^{t}$

的维度大小，

h^t

$h^{t}$

的维度和

x^t

$x^{t}$

的维度都是一维，

h^t

$h^{t}$

的初始值

h^0

$h^{0}$

为全0，

h^t

$h^{t}$

每经过一次

x^t

$x^{t}$

的计算，都会更新，但是

h^t

$h^{t}$

并不是训练的参数，就算损失

loss

$l oss$

一样，都是表征某一个过程的结果。

整个运算过程中，可以训练的参数就是

W

$W$

和

U

$U$

。

nn.RNN还有一个很重要的参数
num_layers
,默认是1，也就是只会有一个

h^t

$h^{t}$

参与到表征字符序列的过程中。这个参数会在下一个部分细说。

从公式上可以看

U

$U$

和

x^t

$x^{t}$

是一个右乘的关系，所以

U

$U$

的作用就是通过与

x^t

$x^{t}$

的矩阵乘法，将tensor的维度大小从

x^t

$x^{t}$

的维度，映射到

h^t

$h^{t}$

的维度。

而

W

$W$

与

h^t

$h^{t}$

也是一个右乘的关系，所以

W

$W$

的作用就是将

h^t

$h^{t}$

的维度大小依然映射到

h^t

$h^{t}$

的维度大小。

所以得出结论，一旦我们创建了一个RNN网络，那么就会出现一个shape=[h,h]的二维tensor

W

$W$

，和一个shape=[h,u]的二维tensor

U

$U$

这样一来，tanh里面的计算都是一维的计算，即都是shape=[h,]的计算过程，所以自然而言，加入从

h^0

$h^{0}$

开始计算，那么

h^1

$h^{1}$

相当于就是经过计算的

h^0

$h^{0}$

，二者大小保持不变。

其计算流程图可由绘制为：

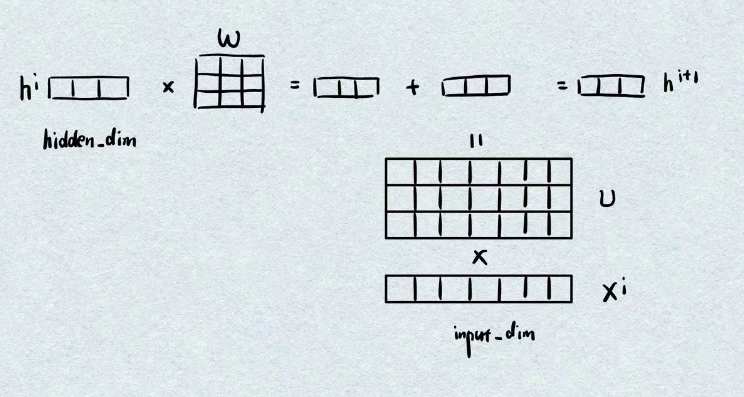
在这里插入图片描述

RNN的输入输出问题

RNN的输入一般为三维的tensor，
shape=[batch,length,input_dim]

nn.RNN中的num_layers表示使用多少个

h^0

$h^{0}$

，但是这几个

h^0

$h^{0}$

并不是独立的，其是输出接输入相互连接的，我们以num_layers=2为例绘制示意图如下：

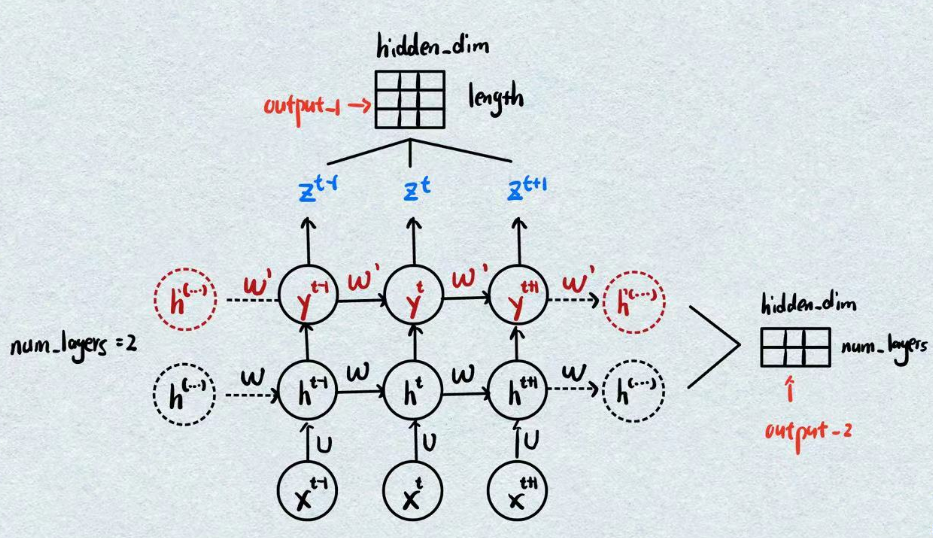
在这里插入图片描述

nn.RNN的输出为两个tensor，即上图中的两个output。

右侧的输出tensor表示
num_layers
个

h^n

$h^{n}$

的输出，之前我们说
num_layers
控制有多少个

h^0

$h^{0}$

，每有一个

h^0

$h^{0}$

，那么经过一个句子以后就会有多少个

h^n

$h^{n}$

，所以当一个句子经过一个
num_layers
个

h^0

$h^{0}$

的RNN网络以后，该部分对应的输出
out_put_2.shape
就是
[num_layers,hidden_dim]

但是有所不同的，batch的位置放在了第一个维度上，即batch个句子经过一个
num_layers
个

h^0

$h^{0}$

的RNN网络以后，该部分对应的输出就是
[num_layers,batch,hidden_dim]
。即第二个输出是一种横向的输出。

nn.RNN向上的输出会包含一个句子里面所有字符对应的输出，是一种纵向的输出，它不会管你使用(也可以说堆叠了)多少个

h^0

$h^{0}$

，它只会输出最后一个

h^0

$h^{0}$

经过每个“字符”以后，每个“字符”对应的输出（图上所有的

h

$h$

或者

y

$y$

其实都是一回事，只不过所处位置不同而已)

所以
out_put_1.shape=[length,hidden_dim]

其batch是摆在第0个维度的，所以扩展为
out_put_1.shape=[batch,length,hidden_dim]

总结一下

两个输出，两个output的最后一个维度大小都是hidden_dim
output_1保存了每个字符输出的最后的信息，所以另一个维度为length
output_2保存了每一层
$h^0 h 0 对应的最后的输出，所以另一个维度为num_layers$
output_1的batch在第0个维度，output_2的batch在第1个维度上

nn.RNN中的bidirectional参数

按照序列本身的顺序是存在一个

W

$W$

和一个

U

$U$

的，可以理解为用来学习序列的正向规律，那么我们同样可以再设置一个

W

$W$

和一个

U

$U$

来学习序列的反向规律，这就是
bidirectional
参数的作用。其使用方法再最后一节中进行介绍。

nn.RNN使用时还需要注意的问题

第一个是nn.RNN里面的另一个参数
batch_first
，怪就怪在它默认是False，即如果我们输入的字符形式为
[bacth,length,input_dim]
，那么它会默认length的位置才是batch，所以一般都必须单独设置为True

第二个则是输入句子的长度，因为我们训练的权重只有

W

$W$

和

U

$U$

,而这两个与句子的长度没有关系，所以允许测试和训练的时候使用不同长度的句子，区别只不过在于RNN计算的次数而已。

nn.RNN使用时常用的格式

import torch.nn as nn
import torch

embed=nn.Embedding(1000,300)

rnn=nn.RNN(input_size=300,hidden_size=256,num_layers=3)

words=torch.tensor([[2,5,6,7],[5,6,7,8]],dtype=torch.long)

input=embed(words)
input=torch.permute(input,dims=[1,0,2])

output,h0=rnn(input)
print(output.shape)#[4,2,256]
print(h0.shape)#[3,2,256]

我们默认将输入的tensor中的序列数放在最外面的维度上，那么实际我们只需要关注输出的最外面的维度。

当我们想要每个字符对应的输出的时候，那么就输出第一个

当我们想要每一层对应的输出的时候，那么就输出第二个

如果设置
bidirectional
参数，那么省略掉相同的代码，演示为：

rnn=nn.RNN(input_size=300,hidden_size=256,num_layers=3)

output,h0=rnn(input)
print(output.shape)#[4,2,512]
print(h0.shape)#[6,2,256]

当我们想要输出每个字符对应的输出的时候，由于正向有一套输出，反向也有一套输出，所以将这两个输出进行堆叠，就得到了每个字符的总输出，故最后一个维度上会翻倍

当我们想要输出每一层对应的输出的时候，由于每一层此时对应正向一个输出，反向一个输出，故每一层实际对应两个输出，但是不同于字符输出，其并不会在最后一个维度上翻倍，而是相当于只增加输出的数量，即在第0个维度上进行堆叠。

LSTM的计算流程

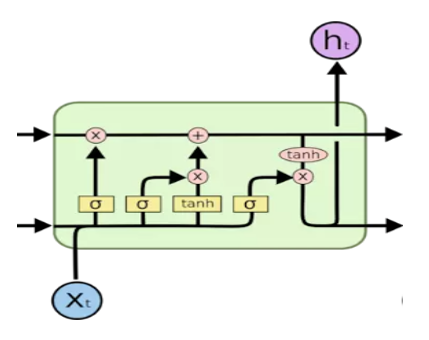
在这里插入图片描述

LSTM的目的是更有效率地进行信息的更新，因为我们最后传递的仅仅是隐藏变量

h

$h$

，在LSTM中存在两个隐藏变量

h_l

$h_{l}$

和

h_s

$h_{s}$

，可以理解为长期记忆和短期记忆，其为了解决的问题是：隐藏变量

h

$h$

在网络运行期间的长度不会发生变化，但是越往后它承载的信息越多，这显然是不合理的，所以LSTM希望可以“遗忘”部分之前存放的信息以便吸收新的信息，这样

h

$h$

可以更大限度的表征文本的综合信息。

所以为什么这样的结构可以完成上述的要求呢？我们必须梳理一遍它里面计算流程，我们假设
input_dim=12,hidden_dim=7

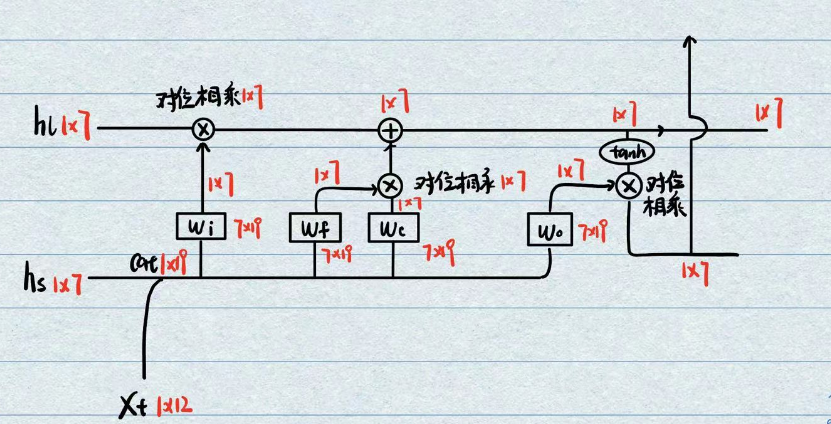
在这里插入图片描述

一个LSTM中需要训练的矩阵有四个

W_i,W_f,W_c,W_o

$W_{i}, W_{f}, W_{c}, W_{o}$

,可以理解为就是4个全连接层。

这四个全连接层的目的就是将负责处理短期记忆的

h_s

$h_{s}$

和此次字符的编码

X_t

$X_{t}$

利用cat结合以后，将维度大小映射回统一长度，方便运算。

那么在一个字符完全参与计算完成以后，其会输出两个经过计算的长期记忆

h_l

$h_{l}$

和短期记忆

h_s

$h_{s}$

LSTM的遗忘和更新原理

关键点就在于流程图中使用的两个激活函数sigmoid和tanh，这两个激活函数的曲线形状非常相像，都是极度容易出现饱和的特征，只不过sigmoid的范围为0到1，tanh的范围是-1到1。

而起到遗忘作用的就是这俩激活函数极度容易饱和的性质，可以理解为关于

X_t

$X_{t}$

两边“多余”的信息无法传递过去，即选择了部分记忆。

而起到更新信息的就是上面简单的对位相加与对位相乘。

所以LSTM整个流程的规律可以描述为：

利用短期记忆

h_s

$h_{s}$

与字符

X_t

$X_{t}$

进行运算，使用sigmoid或tanh激活函数获取字符

X_t

$X_{t}$

的部分信息（遗忘过程）以后，将该信息融合到长期记忆

h_l

$h_{l}$

中（更新过程）

LSTM网络的输入与输出

LSTM和RNN网络的初始化一模一样：↓

lstm=nn.LSTM(input_size=300,hidden_size=256,num_layers=3)

而测试也是一样的过程↓

embed=nn.Embedding(1000,300)
words=torch.tensor([[2,5,6,7],[5,6,7,8]],dtype=torch.long)

input=embed(words)
input=torch.permute(input,dims=[1,0,2])

output,(hl,hs)=lstm(input)
print(output.shape)
print(hl.shape)
print(hs.shape)

lstm返回的是一个output实际也就是rnn中的纵向输出，所以其序列的长度为4，那么这个纵向输出是短期记忆还是长期记忆输出的呢？其实从图中可以看出，它其实是短期记忆，但是也利用tanh获取了部分的长期记忆，即图中的

h_t

$h_{t}$

，然后作为下一个字符输入进来的初始短期记忆。

而由于LSTM中存在两个隐藏变量，所以自然如果选中横向输出，那么自然也会有两个输出，其序列长度自然就是LSTM堆叠的层数

LSTM网络添加bidirectional的输入与输出

output.shape=torch.Size([4, 2, 512])
hl.shape=torch.Size([6, 2, 256])
hs.shape=torch.Size([6, 2, 256])

其结构与RNN一模一样

当我们选择双向输出的时候每个字符相当于会输出两个方向的短期记忆，所以output的最后一个维度大小翻倍

但是，每个短期与长期记忆正反向共享，其维度保持不变。

GRU的运算流程与使用规则

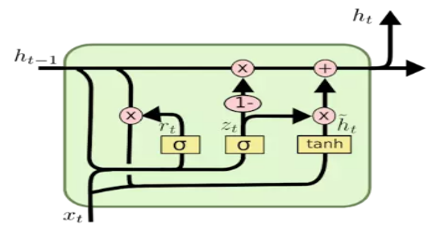
在这里插入图片描述

GRU相对于LSTM来说，减少了训练的参数，其训练的全连接层只有三个（其实只需要看这个流程中有多少个黄色框就有多少个全连接层）

它的隐藏层重新回归到了一个，所以它的计算流程就按照图上来就可以了

它的初始化和RNN以及LSTM一模一样，其输出格式与RNN一模一样，所以并没有需要太多讲述的东西。

原文链接：https://blog.csdn.net/weixin_44586881/article/details/130930850