在上一节我们已经讲过了怎么使用快慢指针去寻找链表的中点,这一节我们继续学习快慢指针的进阶用法,快慢指针不仅仅用在链表中,而是一种代码思想哦,好好体会吧
为了测试的方便我们先创建ListNode类,补充创建方法和打印方法:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
#用于创建链表的类
@staticmethod
def create(list):
dummy=ListNode(0)
cur=dummy
for i in list:
cur.next=ListNode(i)
cur=cur.next
return dummy.next
#用于打印链表的类
@staticmethod
def printList(head):
if head is None:
print("None")
#这里的return不返回任何值,让程序不执行下面的代码,直接结束
return
cur=head
#拼接字符串然后输出
info="LinkedList:"
while cur:
info+=str(cur.val)+"->"
cur=cur.next
#strip函数用于删除字符串两端的指定字符
deal_info=info.strip("->")
print(deal_info)测试结果如下: LinkedList:1->2->3->4->5
删除链表的倒数第N个节点

解法一
要删除链表的第N个节点,朴素点的解法是通过第一次遍历获得当前链表的总个数,然后根据倒数第n个节点进行反推,删除掉指定节点,即便是朴素解法这道题也有小坑:
-
因为
链表可以被完全删除
,例如示例2,链表总共就只有一个节点,删除了的话则应该返回空 -
怎样
删除链表的头节点
?
以上两个小坑可以采用虚拟节点这个技巧来避免,虚拟指针一般命名为dummy,连接在头节点的前面来对链表进行管理,如下图所示:
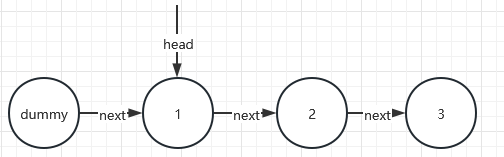
为什么使用虚拟节点?
为了防止空指针的出现,比如链表有5个节点,让你删除倒数第5个节点,按照算法逻辑,首先该找到倒数第6个节点,但是第六个节点已经不存在了,这就会导致程序访问了None节点的属性next,也就导致了空指针异常的出现,如果我们增加一个dummy实体节点,是否就避免了这种情况的出现
先自己做一做哈,代码以及测试如下:
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
#子函数的声明,getLength获得链表的长度
def getLength(head: ListNode) -> int:
length = 0
while head:
length += 1
head = head.next
return length
#这里开始是主要代码
dummy = ListNode(0, head)#建立虚拟节点
length = getLength(head)#获取长度
cur = dummy
#找到被删除的节点的前一个节点
for i in range(1, length - n + 1):
cur = cur.next
#删除操作
cur.next = cur.next.next
return dummy.next
#测试代码
obj=Solution()
list1=ListNode.create([1])
list2=ListNode.create([1,2,3])
list3=ListNode.create([1,2,3,4,5])
head1=obj.removeNthFromEnd(list1,1)
ListNode.printList(head1)
head2=obj.removeNthFromEnd(list2,3)
ListNode.printList(head2)
head3=obj.removeNthFromEnd(list3,3)
ListNode.printList(head3)测试结果:
NoneLinkedList:2->3
LinkedList:1->2->4->5
解法二
终于要开始介绍快慢指针的解法了,这里需要用到一点数学思维: 我们先将fast指针放在比slow指针快n个的位置上,当fast到达了中点,那么slow就到达了我们想要的位置呢?
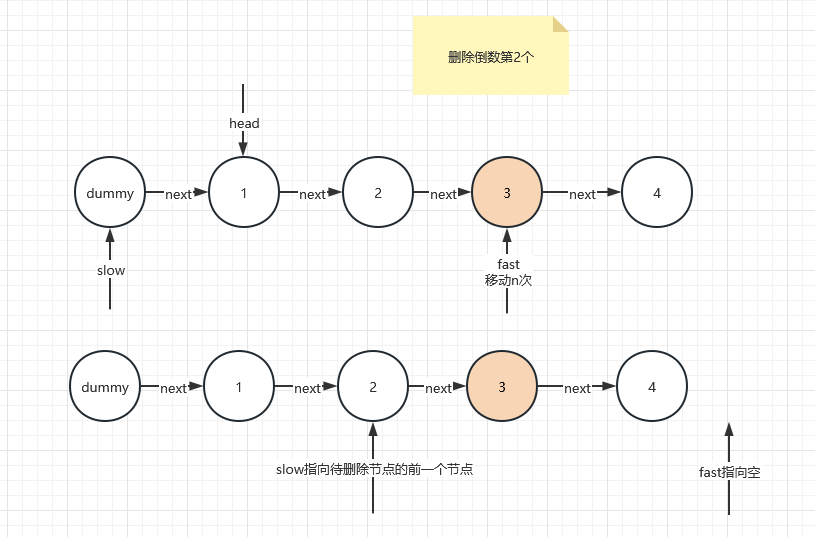
根据以上图示写一写代码吧
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
dummy = ListNode(0, head)
fast = head
slow = dummy
for i in range(n):
fast = fast.next
while fast:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return dummy.next
环形链表
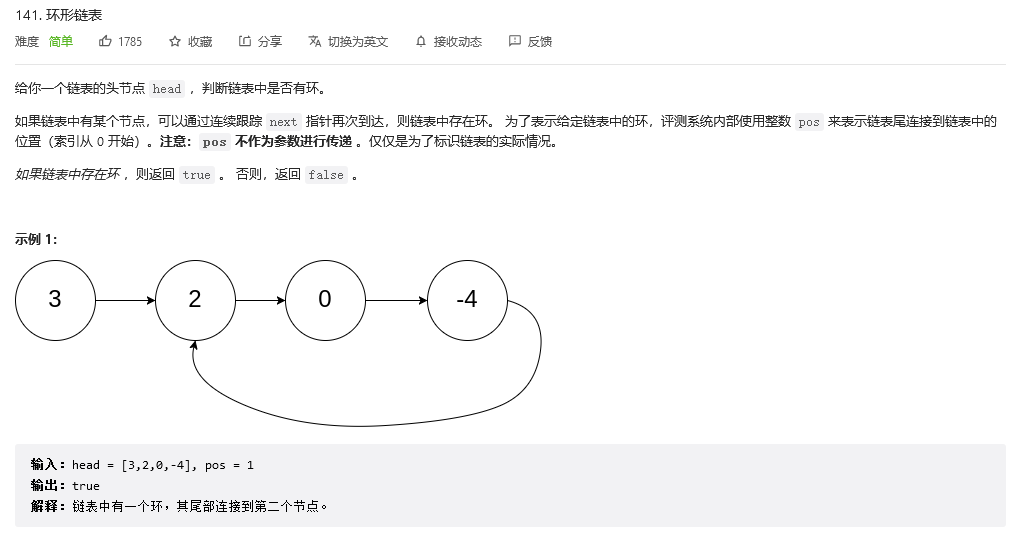
环的概念是这样的比如1.next=2 2.next=3然后3.next=1, 我们通过遍历链表的方式是不是永远都没办法从这个环里走出去,看看能不能自己使用快慢指针想到思路(和寻找链表的中点很像哦),如果链表有环就返回true,否则就返回false
神奇的分割线————————————————————————————————————
思路是这样的,我们使用slow指针每次走一步,fast指针每次走两步,如果是环的话,那么slow和fast是否一定有相等的时候,如果不是则fast指针就会提前指向空,知道了思路再试试看代码怎么写吧
神奇的分割线————————————————————————————————————
class Solution:
def hasCycle(self, head: ListNode) -> bool:
if not head or not head.next:
return False
slow = head
fast = head.next
while slow != fast:
if not fast or not fast.next:
return False
slow = slow.next
fast = fast.next.next
return True
环形链表2
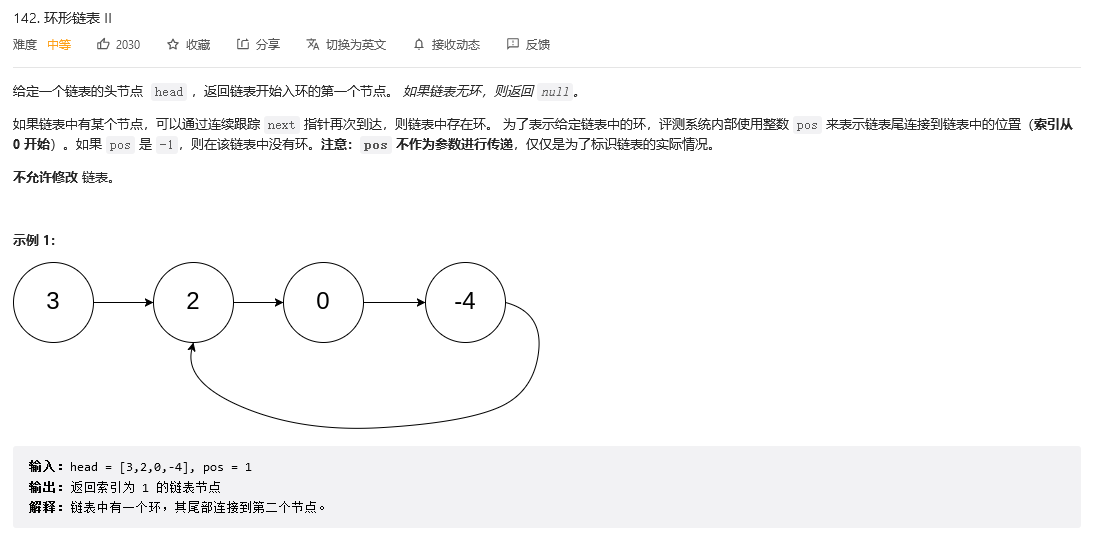
emmmmm,相比于上题更难了一点,因为不仅要判断有没有环还需要返回环的入口位置,这里又涉及到了一个数学知识了,而且还需要重置快慢指针,先看看自己能不能想出来吧
神奇的分割线————————————————————————————————————
思路在这里!!
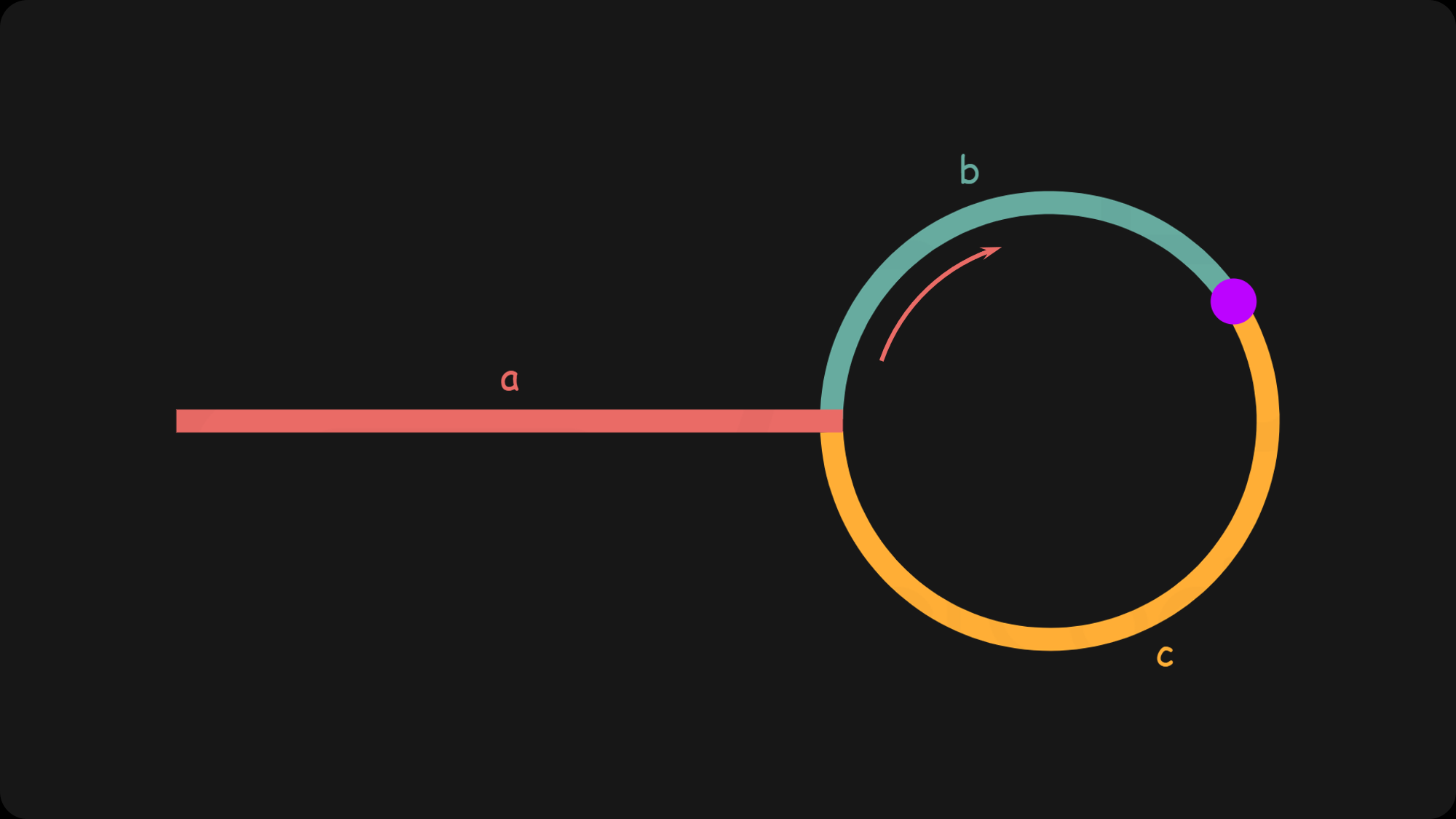
我们观察一下上面这幅图,紫点定义为快慢指针相遇的点,两个指针按照顺时针在环里运动,slow指针每次移动1步,fast指针每次移动2步,那么到达紫点的时候,我们分别计算slow和fast移动过的距离:
- slow: distance = a+b
- fast: distance = a+b+n(b+c)
是不是有点抽象,其实用文字来描述就是”slow进入环后,走了b距离与fast相遇,
此时fast已经在环中走过了n圈
“,根据我们的初始条件fast走过的距离为slow的两倍,则有:
- n(b+c)=a+b 则有a=n(b+c)-b=c+(n-1)(b+c)
发现了吗? b+c刚好就是一个环的长度,a和c是什么,a是进入环要走的路,c是到达相遇点后还需要走的路,我们发现他们的差值就是环的倍数
此时slow和fast指针都在紫点处,如果我们移动其中一个指针到链表头部(a开始的地方)让他们同时走,走同样的步数再相遇,是否就找到了环的入口
神奇的分割线————————————————————————————————————
代码如下:
class Solution(object):
def detectCycle(self, head):
fast, slow = head, head
while True:
if not (fast and fast.next): return
fast, slow = fast.next.next, slow.next
if fast == slow: break
fast = head
while fast != slow:
fast, slow = fast.next, slow.next
return fast这里可别用我们的create函数去创建环形链表哦,得自己一个一个写类似于:
node1=ListNode(1)
node2=ListNode(2)
node3=ListNode(3)
node1.next=node2
node2.next=node3
node3.next=node2
课后作业
终于来到了久违的课后作业环节,其实这题和环形链表2很像,看看你能不能自己做出来吧