




from sklearn.linear_model import Ridge,LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
# 导入数据
data_x=[]
data_y=[]
f=open('E:\Desktop\python_code\sklearn\课程数据\回归\prices.txt','r')
lines=f.readlines()
for line in lines:
items=line.strip().split(',') #line.去掉(空格).分割(',')
data_x.append(int(items[0]))
data_y.append(int(items[1]))
length=len(data_x)
data_x=np.array(data_x).reshape([length,1])
data_y=np.array(data_y)
# 划分训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(data_x,data_y,random_state=0)
# 三个岭回归和一个线性回归模型
linear = LinearRegression().fit(X_train,y_train)
ridge1 = Ridge().fit(X_train,y_train)
ridge2 = Ridge(alpha=100,).fit(X_train,y_train)
ridge3 = Ridge(alpha=10000).fit(X_train,y_train)
# 打印3个岭回归的训练集、测试集得分,以及线性系数和与y轴坐标
print ("training set score:{:.2f}".format(ridge1.score(X_train,y_train)))
print ("test set score:{:.2f}".format(ridge1.score(X_test,y_test)))
print('Coefficients:',ridge1.coef_)
print('intercept:',ridge1.intercept_)
print ("training set score:{:.2f}".format(ridge2.score(X_train,y_train)))
print ("test set score:{:.2f}".format(ridge2.score(X_test,y_test)))
print('Coefficients:',ridge2.coef_)
print('intercept:',ridge2.intercept_)
print ("training set score:{:.2f}".format(ridge3.score(X_train,y_train)))
print ("test set score:{:.2f}".format(ridge3.score(X_test,y_test)))
print('Coefficients:',ridge3.coef_)
print('intercept:',ridge3.intercept_)
print ("training set score:{:.2f}".format(linear.score(X_train,y_train)))
print ("test set score:{:.2f}".format(linear.score(X_test,y_test)))
print('Coefficients:',linear.coef_)
print('intercept:',linear.intercept_)
从上往下依次为
3个岭回归
alpha=0
alpha=100
alpha=10000
1个线性回归
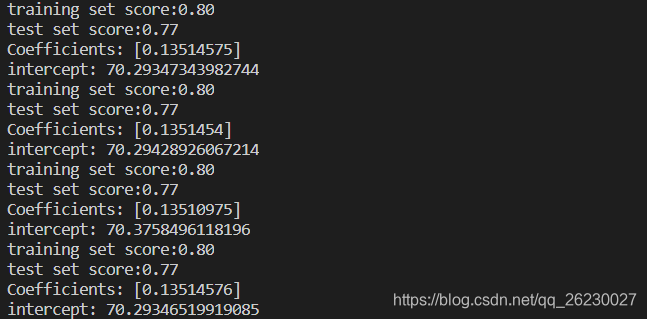
α越大,那么正则项惩罚的就越厉害,得到回归系数就越小。
α越小,即正则化项越小,那么回归系数就越来越接近于普通的线性回归系数。
应用


import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge#加载岭回归方法
from sklearn import model_selection
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures #用于创建多项式特征,如ab、 a2、 b2
data=pd.read_csv('E:\Desktop\python_code\sklearn\课程数据\回归\岭回归.csv')
#绘制车流量信息
plt.plot(data['TRAFFIC_COUNT'])
plt.show()
X=data[data.columns[1:5]]#属性数据
y=data['TRAFFIC_COUNT']#车流量数据(即是要预测的数据)
poly=PolynomialFeatures(5)#测试后5是效果较好的一个参数
#X为创建的多项式特征
X=poly.fit_transform(X)
#将所有数据划分为训练集和测试集,test_size表示测试集的比例,random_state是随机数种子
train_set_X, test_set_X , train_set_y, test_set_y = model_selection.train_test_split(X,y,test_size=0.3,random_state=0)
#创建岭回归实例
clf=Ridge(alpha=1.0,fit_intercept = True)
#调用fit函数使用训练集训练回归器
clf.fit(train_set_X,train_set_y)
#利用测试集计算回归曲线的拟合优度,clf.score返回值为0.7375
#拟合优度,用于评价拟合好坏,最大为1,无最小值,当对所有输入都输出同一个值时,拟合优度为0。
clf.score(test_set_X,test_set_y)
start=200 #接下来我们画一段200到300范围内的拟合曲线
end=300
y_pre=clf.predict(X) #是调用predict函数的拟合值
time=np.arange(start,end)
plt.plot(time,y[start:end],'b', label="real")
plt.plot(time,y_pre[start:end],'r', label='predict')
#展示真实数据(蓝色)以及拟合的曲线(红色)
plt.legend(loc='upper left') #设置图例的位置
plt.show()
版权声明:本文为qq_26230027原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。