目录
线程池没有空闲线程时,新的任务请求线程资源时,线程池该如何处理?各种处理策略又是如何实现的呢?
本文是王争老师的《算法与数据结构之美》的学习笔记,详细内容请看王争的专栏 。
队列
队列的概念
队列和栈类似,也是一种特殊的线性表。和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作。(
先进先出
)
顺序队列和链式队列
跟栈一样,用数组实现的队列叫作
顺序队列
,用链表实现的队列叫作
链式队列
。
// 用数组实现的队列
public class ArrayQueue {
// 数组:items,数组大小:n
private String[] items;
private int n = 0;
// head表示队头下标,tail表示队尾下标
private int head = 0;
private int tail = 0;
// 申请一个大小为capacity的数组
public ArrayQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
// 入队
public boolean enqueue(String item) {
// 如果tail == n 表示队列已经满了
if (tail == n) return false;
items[tail] = item;
++tail;
return true;
}
// 出队
public String dequeue() {
// 如果head == tail 表示队列为空
if (head == tail) return null;
// 为了让其他语言的同学看的更加明确,把--操作放到单独一行来写了
String ret = items[head];
++head;
return ret;
}
}
对于栈来说,只需要一个
栈顶指针
就可以了。但是队列需要两个指针:一个是
head 指针
,指向队头;一个是
tail 指针
,指向队尾。
当 a、b、c、d 依次入队之后,队列中的 head 指针指向下标为 0 的位置,tail 指针指向下标为 4 的位置.
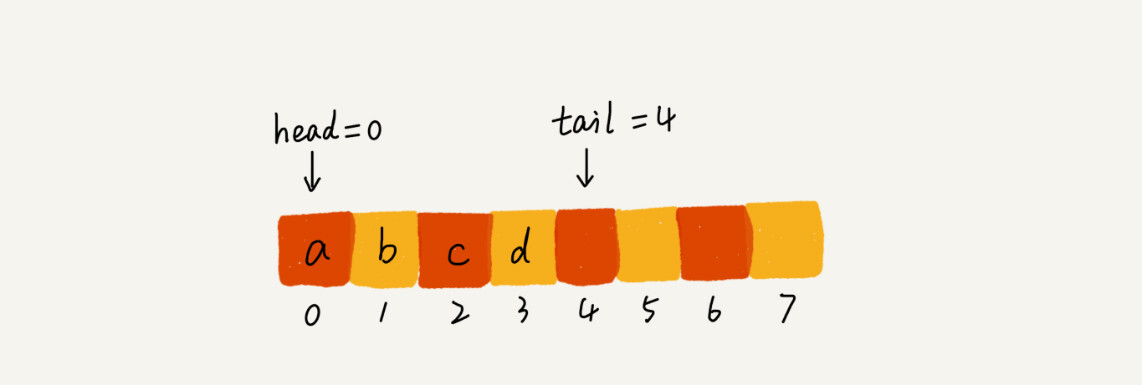
当调用两次出队操作之后,队列中 head 指针指向下标为 2 的位置,tail 指针仍然指向下标为 4 的位置。
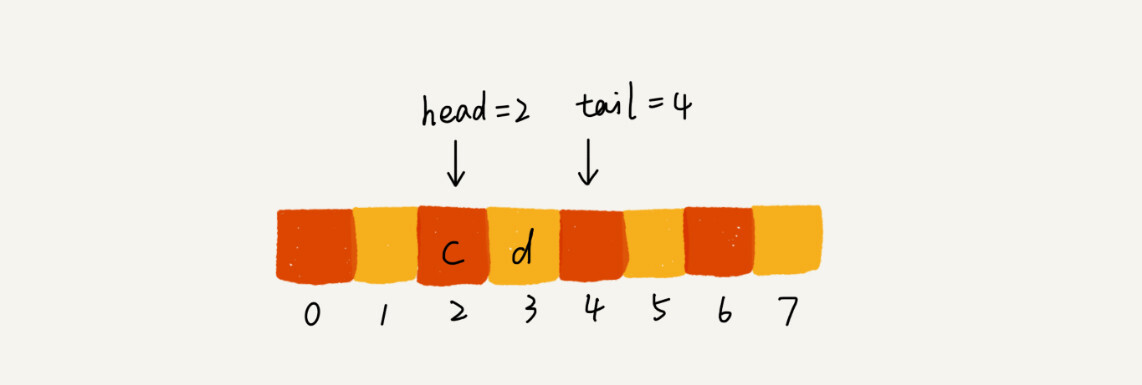
你肯定已经发现了,随着不停地进行入队、出队操作,head 和 tail 都会持续往后移动。当
tail 移动到最右边
,即使数组中还有空闲空间,也无法继续往队列中添加数据了。这个问题该如何解决呢?
为解决数组的删除操作会导致数组中的数据不连续的问题,有方法–
数据搬移
。
每次进行出队操作都相当于删除数组下标为 0 的数据,要搬移整个队列中的数据,这样
出队操作的时间复杂度就会从原来的 O(1) 变为 O(n)
。
优化上述操作,实际上,在出队时可以
不用搬移数据
。如果没有空闲空间了,我们只需要在入队时,再集中触发一次数据的搬移操作。借助这个思想,出队函数 dequeue() 保持不变,我们稍加改造一下入队函数 enqueue() 的实现。
// 入队操作,将item放入队尾
public boolean enqueue(String item) {
// tail == n表示队列末尾没有空间了
if (tail == n) {
// tail ==n && head==0,表示整个队列都占满了
if (head == 0) return false;
// 数据搬移
for (int i = head; i < tail; ++i) {
items[i-head] = items[i];
}
// 搬移完之后重新更新head和tail
tail -= head;
head = 0;
}
items[tail] = item;
++tail;
return true;
}
当队列的 tail 指针移动到数组的最右边后,如果有新的数据入队,可以将 head 到 tail 之间的数据,整体搬移到数组中 0 到 tail-head 的位置。
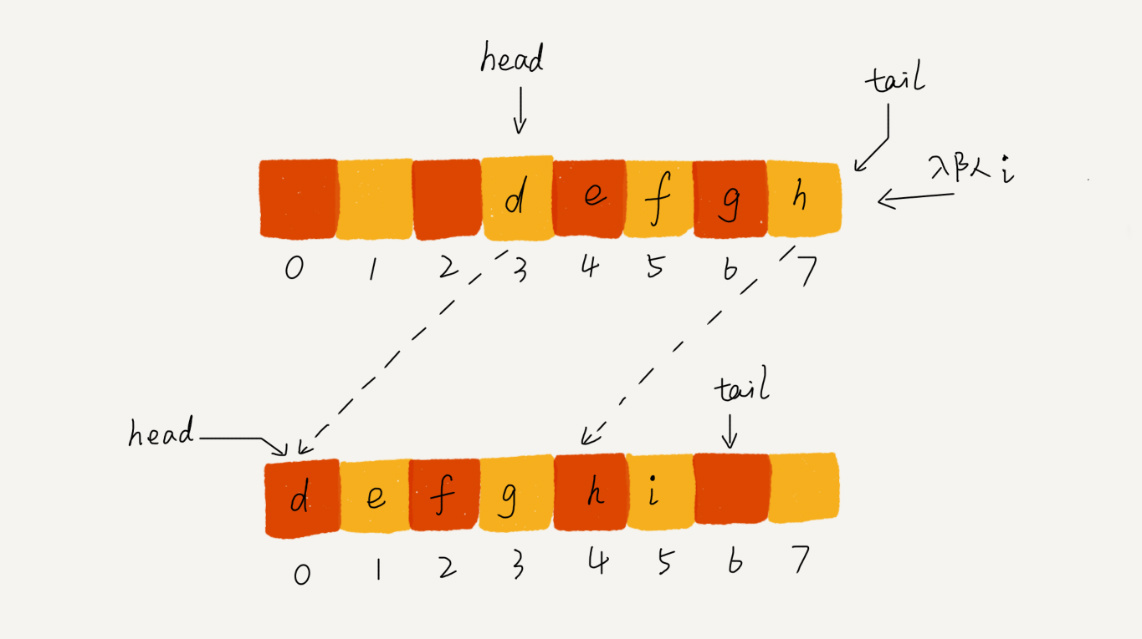
这种实现思路中,
出队操作的时间复杂度仍然是 O(1)
,但入队操作的时间复杂度
最好时间复杂度是O(1)
,
最坏时间复杂度是O(n)
基于链表的队列实现方法
基于链表的实现,同样需要两个指针:head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示,入队时,tail->next= new_node, tail = tail->next;出队时,head = head->next。
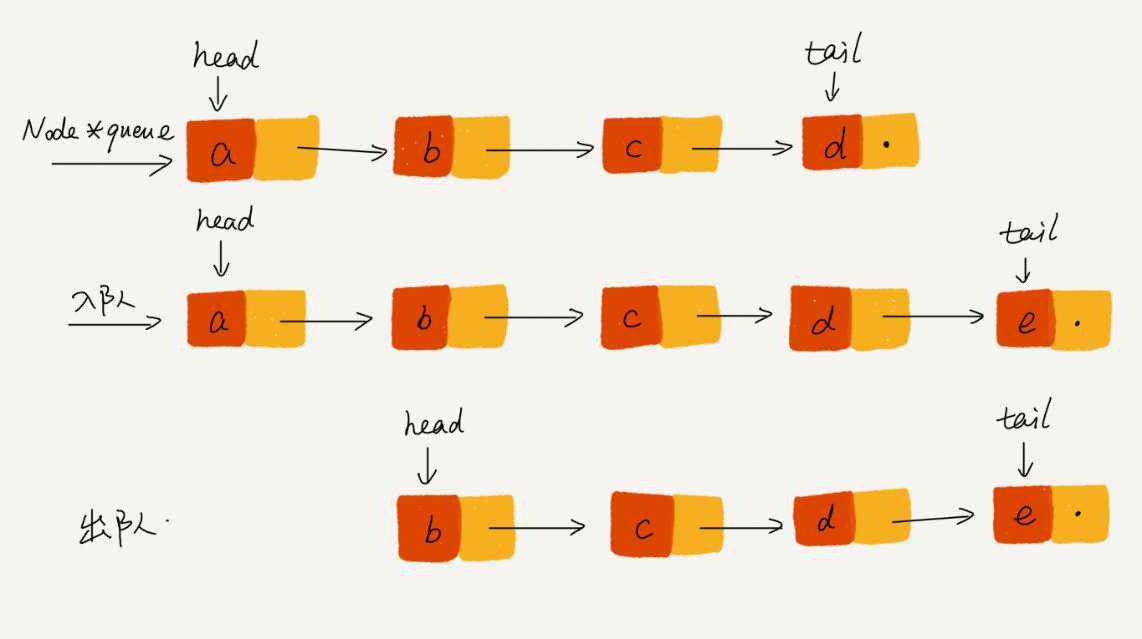
循环队列
刚才用数组来实现队列的时候,在 tail==n 时,会有数据搬移操作,这样入队操作性能就会受到影响.
循环队列,顾名思义,它长得像一个环。原本数组是有头有尾的,是一条直线。现在我们把首尾相连,扳成了一个环。

图中这个队列的大小为 8,当前 head=4,tail=7。
当有一个新的元素 a 入队时,我们放入下标为 7 的位置。但这个时候,并不把 tail 更新为 8,而是将其在环中后移一位,到下标为 0 的位置。
当再有一个元素 b 入队时,我们将 b 放入下标为 0 的位置,然后 tail 加 1 更新为 1。所以,在 a,b 依次入队之后,循环队列中的元素就变成了下面的样子:
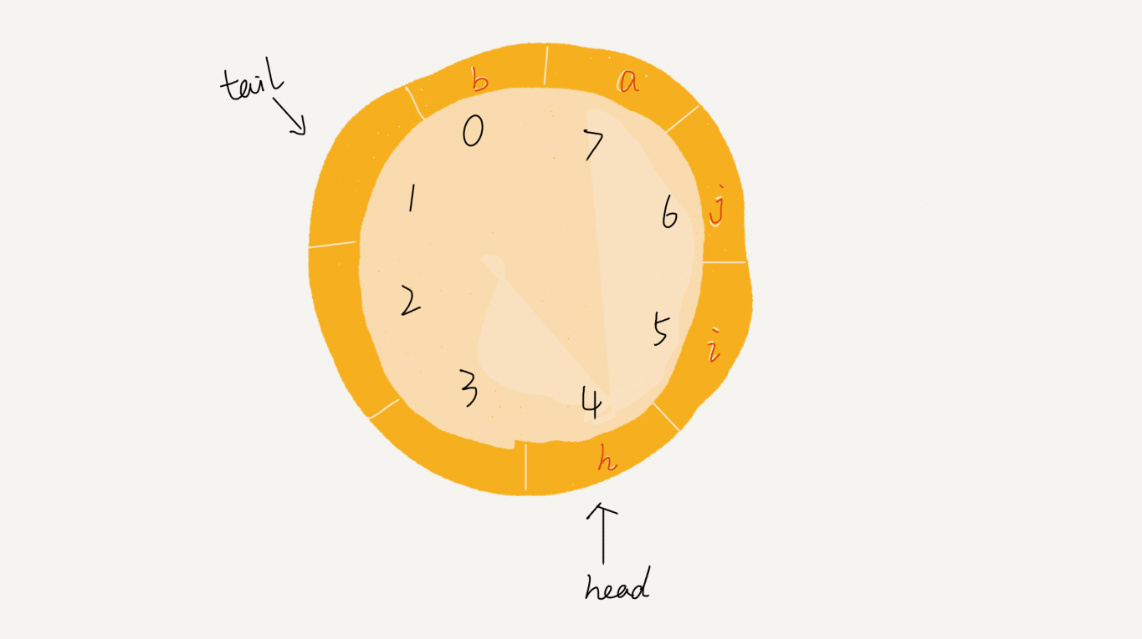
通过这样的方法,成功避免了数据搬移操作。
循环队列的代码实现的关键在于
确定好队空和队满的判定条件
。
在用数组实现的非循环队列中,队满的判断条件是
tail == n
,队空的判断条件是
head == tail
。
对于循环链表,队列为空的判断条件仍然是
head == tail
,队满如下解释。

此时为队满情况,tail=3,head=4,n=8,则队满条件为(3+1)%8=4。
总结出,当队满时,(tail+1)%n=head。
不过,
当队列满时,图中的 tail 指向的位置实际上是没有存储数据的。
所以,
循环队列会浪费一个数组的存储空间。
public class CircularQueue {
// 数组:items,数组大小:n
private String[] items;
private int n = 0;
// head表示队头下标,tail表示队尾下标
private int head = 0;
private int tail = 0;
// 申请一个大小为capacity的数组
public CircularQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
// 入队
public boolean enqueue(String item) {
// 队列满了
if ((tail + 1) % n == head) return false;
items[tail] = item;
tail = (tail + 1) % n;
return true;
}
// 出队
public String dequeue() {
// 如果head == tail 表示队列为空
if (head == tail) return null;
String ret = items[head];
head = (head + 1) % n;
return ret;
}
}
阻塞队列和并发队列
阻塞队列
:就是在队列为空的时候,从队头取数据会被阻塞。因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后再返回。
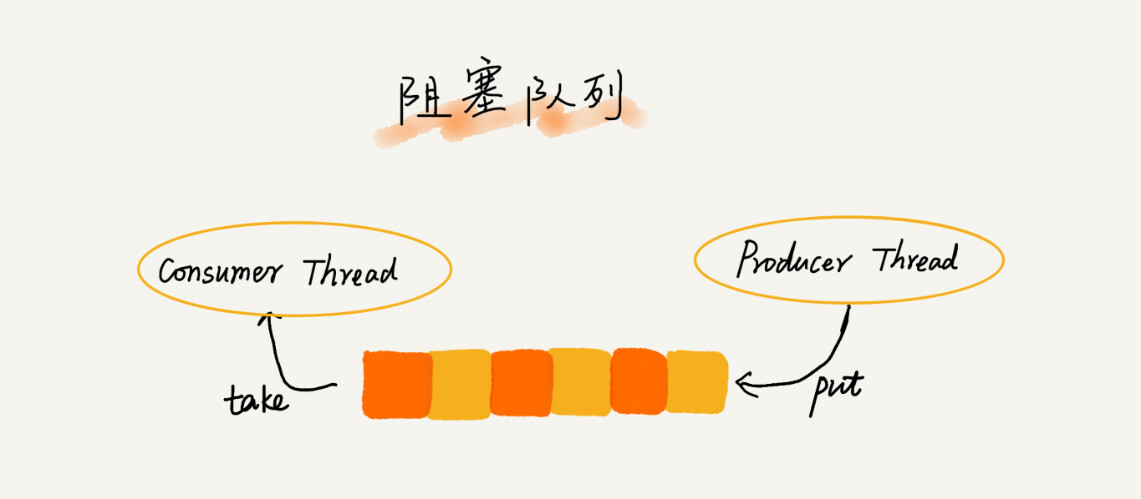
这种基于阻塞队列实现的“
生产者 – 消费者模型
”,可以有效地协调生产和消费的速度。
而且不仅如此,基于阻塞队列,我们还可以通过协调“生产者”和“消费者”的个数,来提高数据的处理效率。
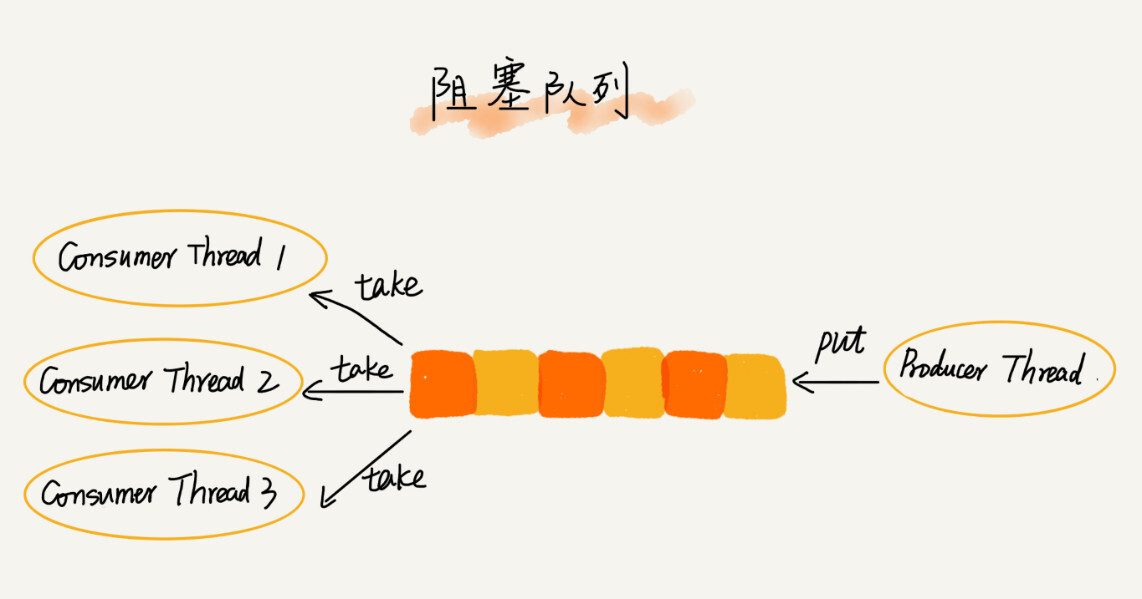
在多线程情况下,会有多个线程同时操作队列,这个时候就会存在线程安全问题
线程安全的队列叫作
并发队列
。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作。实际上,基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。
线程池没有空闲线程时,新的任务请求线程资源时,线程池该如何处理?各种处理策略又是如何实现的呢?
一般有两种处理策略。第一种是非阻塞的处理方式,直接拒绝任务请求;
另一种是阻塞的处理方式,将请求排队,等到有空闲线程时,取出排队的请求继续处理。
我们希望公平地处理每个排队的请求,
先进者先服务
,所以队列这种数据结构很适合来存储排队请求。
队列有基于链表和基于数组这两种实现方式的区别
基于链表的实现方式,可以实现一个支持无限排队的无界队列(unbounded queue),但是可能会导致过多的请求排队等待,请求处理的响应时间过长。所以,针对响应时间比较敏感的系统,基于链表实现的无限排队的线程池是不合适的。
而基于数组实现的有界队列(bounded queue),队列的大小有限,所以线程池中排队的请求超过队列大小时,接下来的请求就会被拒绝,这种方式对响应时间敏感的系统来说,就相对更加合理。不过,设置一个合理的队列大小,也是非常有讲究的。队列太大导致等待的请求太多,队列太小会导致无法充分利用系统资源、发挥最大性能。
队列可以应用在任何有限资源池中,用于排队请求,比如数据库连接池等。
实际上,对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。