参考:
https://blog.csdn.net/weixin_44210987/article/details/113279727
https://blog.csdn.net/qq_36686437/article/details/116369956
https://blog.csdn.net/qq_36686437/article/details/105559280
https://blog.csdn.net/ModestBean/article/details/89438082
三维空间中的曲率:三维曲面偏离平面的程度
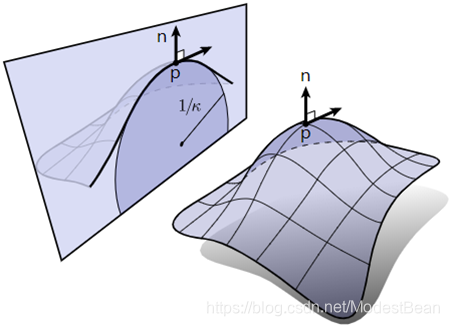
曲面曲率:
在曲面上取一点P,曲面在P点的法线为n,过n可以有无限多个剖切平面,每个剖切平面与曲面相交,交线为一条平面曲线。平面结论:圆上弯曲程度相同,任意一点曲率相等,越弯曲曲率越大,直线曲率为0。
不同的剖切平面上的平面曲线在P点的曲率半径一般是不相等的。
主曲率:曲面上有无数个不同方向的曲线,
曲面上的点不同方向具有不同曲率
,其中最大值和最小值为称为主曲率 k1 和k2,极值方向称为主方向。数学上可证名k1和k2互相垂直。
高斯曲率:两主曲率乘积,反映曲面在不同方向弯曲程度是否相同。高斯曲率为正,为球面。高斯曲率为负双曲面。
平均曲率:两主曲率算数平均数(k1+k2)/2,反映曲面凹凸程度。平均曲率为正,局部凹。平均曲率为负,局部凸。
曲率计算过程:
1. 找出所有的公共边,以及包含他们的两个三角形面片。
保存公共边起始-终点顶点编号(VerticeID, VerticeID)、三角形面片(TriaID,TriaID)编号、单位化的公共边向量edgeVector=[vx, vy,vz] 以及公共边向量长度distances。
2. 求相邻两个三角形面片法向量的cos夹角beta,并符号化。
符号化:
相邻三角形法向量叉乘之后的向量cp,与edgeVector 进行点乘,若结果大于0,sign=1;等于0,sign=0;小于0,sign=-1.
### 右手系法则下,
两个三角形为凸,则cp与edgeVector夹角为0, sign=1;
两个三角形为凹,则cp与edgeVector夹角为180, sign=-1;
两个三角形呈一条线,它们的法向量平行,cp==0, sign=0;
3. 构建曲率公式:
T =f(edgeVector, beta,sign,distance)
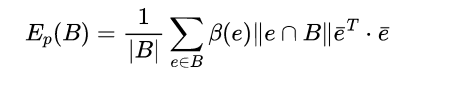
4. 矩阵分解,求特征向量和特征值。
特征值最小的为最小曲率,
特征值最大的为法向量,
特征值第二大的的为最大曲率
Cmean = (Cmin+Cmax)/2
Cgauss = Cmin*Cmax
2. input:
vertices: [nx3]
faces:[n,3]
normals:[n,3]
calculate:
edgeVector:相邻三角形的公共边单位向量。[3,ne], ne为公共边数量
beta:相邻两个三角形法向量的cos角。[1,ne]
Tv:曲率公式
return:
Umin, Umax, Cmin, Cmax, Cmean, Cgauss
依次为最小最大切向量,最小最大曲率,平均曲率,高斯曲率。
import numpy as np
from numpy import linalg as LA
import sys
'''
计算平均曲率和高斯曲率
'''
def getCommonEdges(faces):
'''
input:
faces:[nx3]
return:
commonEdges: indexes of vertices in common edges, [nx2]
facePairs: triangle pairs where they locate in ,[nx2]
'''
# faces = np.array([[1,2,3],[3,2,4],[5,2,1]])
faces = faces-1### python 索引 从 0 开始
numFace = faces.shape[0]
edgeStart = faces.flatten()
edgeEnd = faces[:,[1,2,0]].flatten()
edges = np.vstack((edgeStart, edgeEnd)) #[2,n]
faceId = np.tile(np.arange(numFace),(3,1)).transpose().flatten().tolist()
commonEdges = []
facePires = []
numEdges= edges.shape[1]
for i in range(numEdges):
curEdge = edges[:,i].tolist()
# print(curEdge)
ind1 = np.where(edges[1,:] == curEdge[0])[0]
ind2 = np.where(edges[0,:] == curEdge[1])[0]
index = list(set(ind1).intersection(set(ind2)))
if len(index):
commonEdges.append(curEdge)
facePires.append([faceId[i], faceId[index[0]]])
commonEdges=np.array(commonEdges)
facePires = np.array(facePires)
###### 去除冗余:edgeStart<edgeEnd ################
directioned = np.where(commonEdges[:,0]<commonEdges[:,1])[0]
commonEdges = commonEdges[directioned,:]
facePires = facePires[directioned,:]
return commonEdges, facePires
def getCurvature(vertices, faces, normals):
'''
input:
vertices: [nx3]
faces:[n,3]
normals:[n,3]
calculate:
edgeVector:相邻三角形的公共边单位向量。[3,ne], ne为公共边数量
beta:相邻两个三角形法向量的cos角。[1,ne]
Tv:曲率公式
return:
Umin, Umax, Cmin, Cmax, Cmean, Cgauss
依次为最小最大切向量,最小最大曲率,平均曲率,高斯曲率。
'''
vertices = np.array(vertices).transpose() #[3,n]
normals = np.array(normals).transpose() #[3,n]
numVertices = vertices.shape[1]
### 1. find common edges and corresponding pairs of triangles
commonEdges, facePires = getCommonEdges(faces) #[n,2],[n,2]
ne = commonEdges.shape[0]
#### normalized edge vector #######
edgeStart = commonEdges[:,0]
edgeEnd = commonEdges[:,1]
edgeVector = vertices[:,edgeEnd] - vertices[:,edgeStart] #[3,ne]
distances = np.sqrt(np.sum(edgeVector**2, axis = 0)) #[1,ne]
edgeVector = edgeVector/np.tile(distances,(3,1))
distances= distances/distances.mean()
##### 2. cos angle: beta , 具有公共边的两个三角形法向量的夹角 ############
faceInd1 = facePires[:,0]
faceInd2 = facePires[:,1]
dp = np.sum(normals[:,faceInd1] * normals[:,faceInd2], axis=0)
dp = np.maximum(-1, dp)
dp = np.minimum(1, dp)
beta = np.arccos(dp) #[1,ne]
#### sign: positive or negtive ############
### 右手系法则下,两个三角形为凸,则cp与edgeVector夹角为0, sign=1;两个三角形为凹,则cp与edgeVector夹角为180, sign=-1;
### 两个三角形一条线,它们的法向量平行,cp==0, sign=1;
cp = np.cross(normals[:,faceInd1].transpose(), normals[:, faceInd2].transpose()).transpose()#cp: [3,ne]
sign = np.sign(np.sum((cp * edgeVector), axis=0))
beta = beta*sign
###### 3. 构建曲率函数 ##############
T = np.zeros((3,3,ne))
for i in range(3):
for j in range(3):
T[i,j,:] = np.reshape(edgeVector[i,:]*edgeVector[j,:], (1,1,ne))
T[j,i,:] = T[i,j,:]
###最后的曲率公式如下 ###
T = T * np.tile(np.reshape(distances * beta, (1,1,ne)), (3,3,1))
###### 4. 构建关于所有顶点的矩阵(一个顶点一个通道),并将上述结算结果赋给公共边所含顶点 ###################
Tv = np.zeros((3,3,numVertices))
w = np.zeros((1,1,numVertices))
for k in range(ne):
Tv[:,:,edgeStart[k]] = Tv[:,:,edgeStart[k]] + T[:,:,k]
Tv[:,:,edgeEnd[k]] = Tv[:,:,edgeEnd[k]] + T[:,:,k]
w[:,:,edgeStart[k]] = w[:,:,edgeStart[k]] + 1
w[:,:,edgeEnd[k]] = w[:,:,edgeEnd[k]] + 1
# eps = eps(1) = 2.2204e-16;eps为系统运算时计算机允许取到的最小值
w = np.where(w<sys.float_info.epsilon, 1, w)
Tv = Tv/np.tile(w, (3,3,1))
# ###### 5. smoothing ##############
# for x in range(3):
# for y in range(3):
# a = Tv[x,y,:]
# a = meshSmoothing(faces,vertices,a(:),options)
# Tv[x,y,:] = a
###### 6. 矩阵分解:求特征向量eigenvectors and 特征值eigenvalues ###############
U = np.zeros((3,3,numVertices))
D = np.zeros((3,numVertices))
for k in range(numVertices):
[d, u] = LA.eig(Tv[:,:,k])
d = np.real(d)
### sort: 按照特征值的绝对值从小到大排序 ######
sortedInd = sorted(range(len(d)), key=lambda k: abs(d)[k])
D[:,k] = d[sortedInd]
U[:,:,k] = np.real(u[:,sortedInd])
Umin =np.squeeze(U[:,2,:]) #### [3,n]
Umax = np.squeeze(U[:,1,:]) #### [3,n]
Cmin = D[1,:].transpose() #### [1,n]
Cmax = D[2,:].transpose() #### [1,n]
Cmean = (Cmin+Cmax)/2
Cgauss = Cmin*Cmax
Normal = np.squeeze(U[:,0,:])
return Umin, Umax, Cmin, Cmax, Cmean, Cgauss
if __name__=='__main__':
from readData.objParser import *
modelFile ='building2-1/components/pillar1.obj'
###### 数据解析 ########################
objParser = OBJ_PARSER(modelFile)
faces = objParser.get_faces()
faces = np.array(faces)[:,[0,2,4]]
vertices = objParser.get_vertices()
vertices = np.array(vertices).astype(np.float64)
normals = objParser.get_normals()
########### 计算曲率 #####################
Umin, Umax, Cmin, Cmax, Cmean, Cgauss = getCurvature(vertices, faces, normals)