进位计数制

基数的概念：

进位计数制中表示一位数所能使用的数码符号个数。

如：十进制数中有0-9共10个数码，则基数为10，逢10就进1。

位权或权的概念：

（1）任何的一个数，不同数位的数码表示的值的大小不同。

如十进制的343，第一个3表示300，第三个3表示3。

（2）每个数位的数码代表的数值，等于数码乘以一个固定数值，这个数值称为位权或权。

（3）任何一种进位计数制表示的数都可以拆分

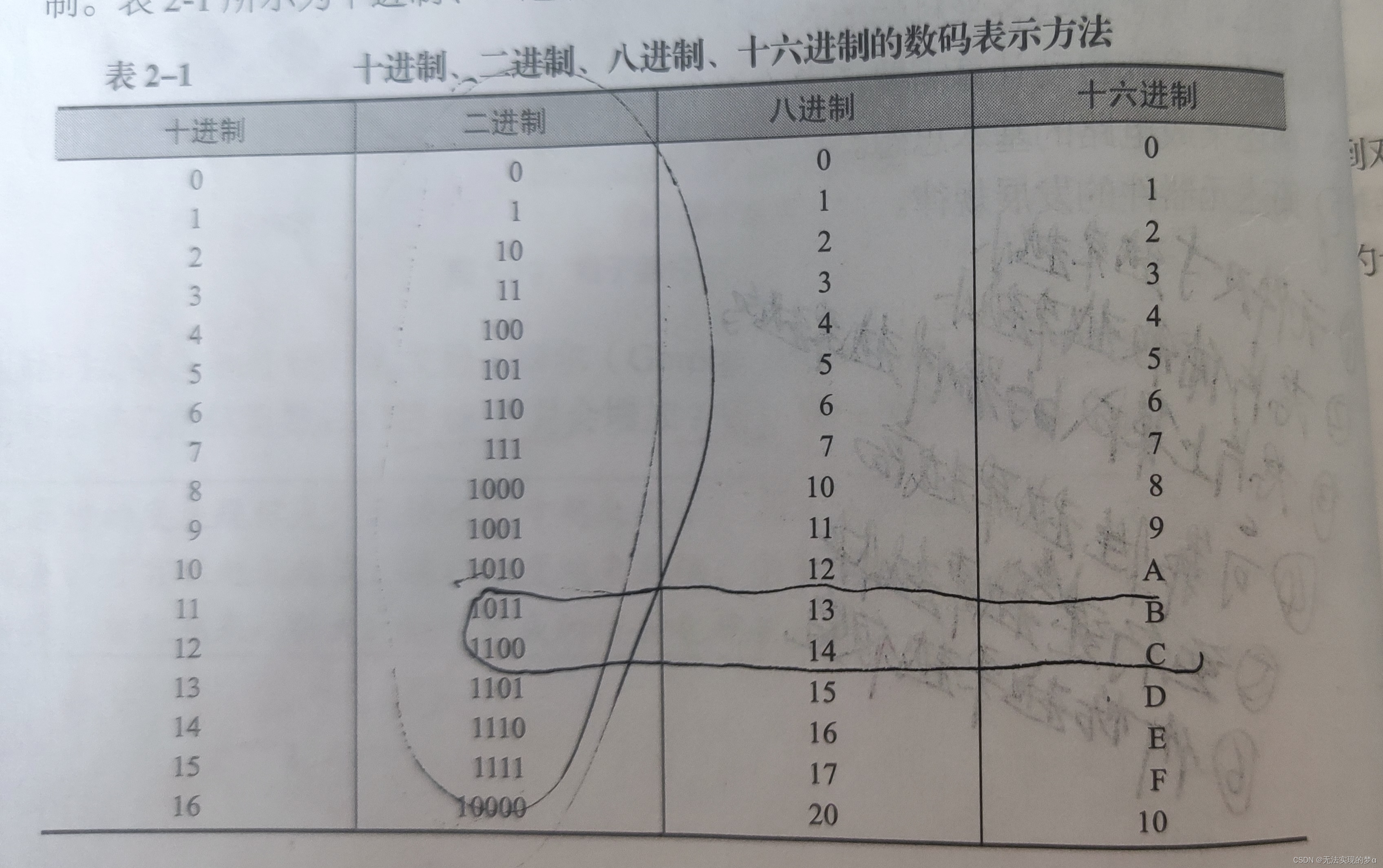
不同进制数的转换

不同进制数转换成十进制数：

用每个位置上的数码乘以相应的位权，然后求和，就可以得到对应的十进制数。

十进制数转换为二进制数、八进制数、十六进制数：

（1） 将十进制数的整数部分转换为R进制，采用除R取余法：除以R取余数，将商反复除以R，直到商为0。

（2）得到的第一个余数为最低位，最后一个余数为最高位，然后将余数从高位到低位依次排列即可。

二进制、八进制、十六进制数间的相互转换：

每3位二进制数对应1位八进制数、每4位二进制数对应1位十六进制数。

二转八：从小数点开始向两边，3位二进制数换成1位八进制数，开始和结尾不足的部分补0即可。

二转十六与之类似。

八进制、十六进制转为二进制：

方法与上面类似，省略开头和结尾的0即可。

上面的红字部分是用来计算对应的十进制数，掌握这个方法以后就不用查表了！！！递增规律为：1、2、4、8、16、32、64、、、在1的地方写上对应位置的数相加即可得到对应的十进制数。如：8+4+2=14。