标注一下,这是从我的课程设计实验报告中复制粘贴过来的,希望对大家有所帮助
解题思路:利用二维数组的前缀和求解
算法描述:
定义一个二维数组arr[301][301],用来存放数组元素,再定义一个二维数组sum[301][301],其中
sum[a][b]=所有a[i][j]的和,0<=i<=a,0<=j<=b
。可以很容易知道:
sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j]
显然sum[0][0]是不能被计算的,所以在这里i和j均从1开始循环,每输入一个数组元素arr[i][j],就计算一次sum[i][j]。
需要注意的是,arr数组和sum数组都应该被初始化为0,如此,这两个数组的第0行和第0列就都是0了,利用公式计算sum[i][j]时才不会出问题。
由于i和j都是从1开始循环的,所以有效元素是从arr[1][1]开始的,又因为arr和sum数组的第0行和第0列就都是0,所以即使访问到了sum[i-1][j],sum[i][j-1]和sum[i-1][j-1]也没有问题,反正加减的都是0。如果行和列都被定义为300,并且i和j都从0开始的话,套用上面的公式就要分情况讨论,略显繁琐。
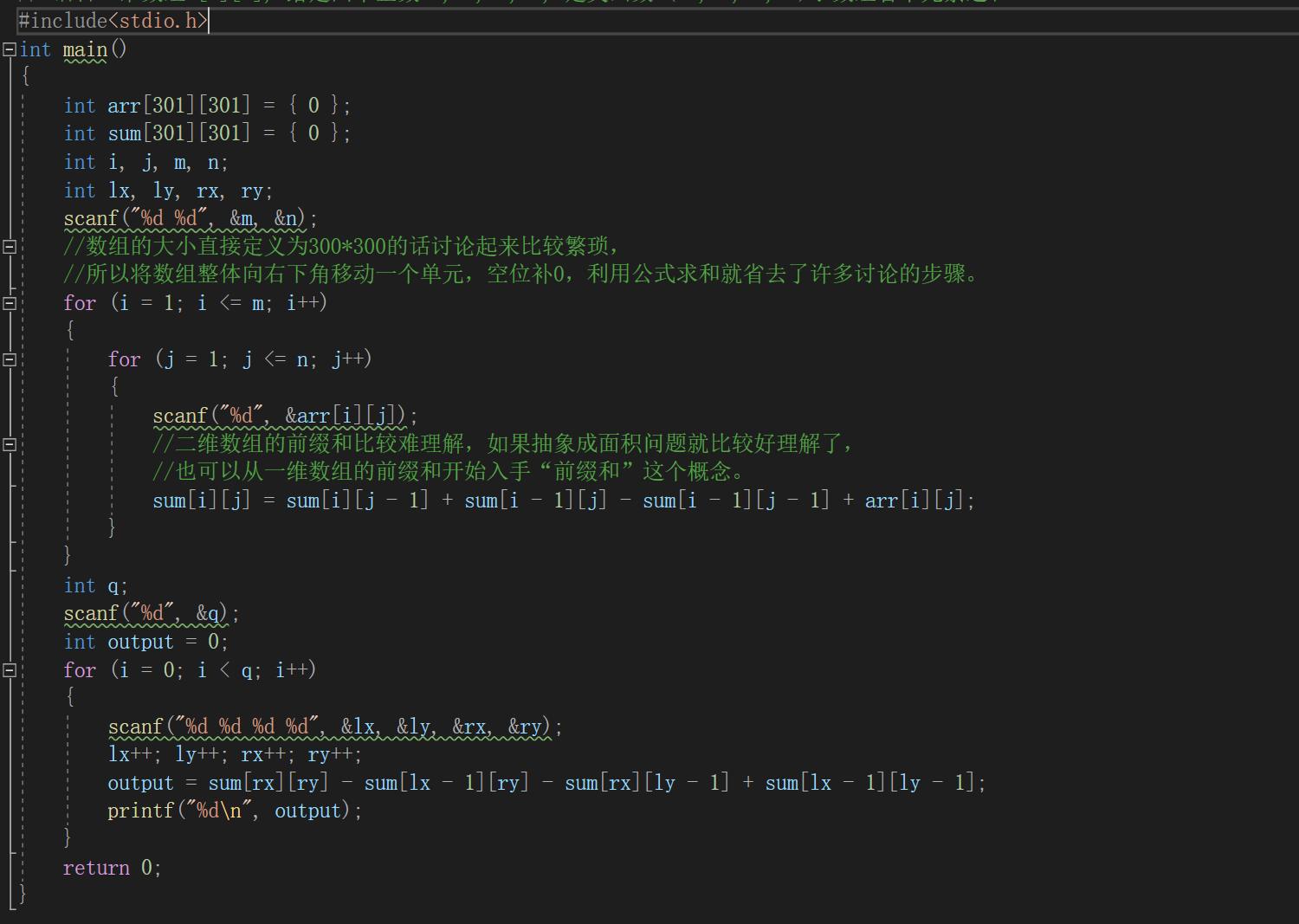
这里有个前缀和的概念,一维数组的前缀和其实就类似于数列求和,
sum[n] = a[0]+a[1]+……+a[n]
对于二维数组
sum[n][m] = a[0][0]+a[0][1]+a[1][0]+a[1][1]+……+a[n][m]
sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j]
-
就比如有下面一个二维数组
|
a[0][0] |
a[0][1] |
a[0][2] |
a[0][3] |
|
a[1][0] |
a[1][1] |
a[1][2] |
a[1][3] |
|
a[2][0] |
a[2][1] |
a[2][2] |
a[2][3] |
|
a[3][0] |
a[3][1] |
a[3][2] |
a[3][3] |

比如求个sum[3][3],上图红框就是sum[3][3],蓝框是sum[3-1][3],绿框是sum[3][3-1],黑框是sum[3-1][3-1]
很容易就看出sum[3][3] = sum[3-1][3] + sum[3][3-1] – sum[3-1][3-1] + a[3][3]
以此类推就可以得出
sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j]
了