目录

1 信号的产生

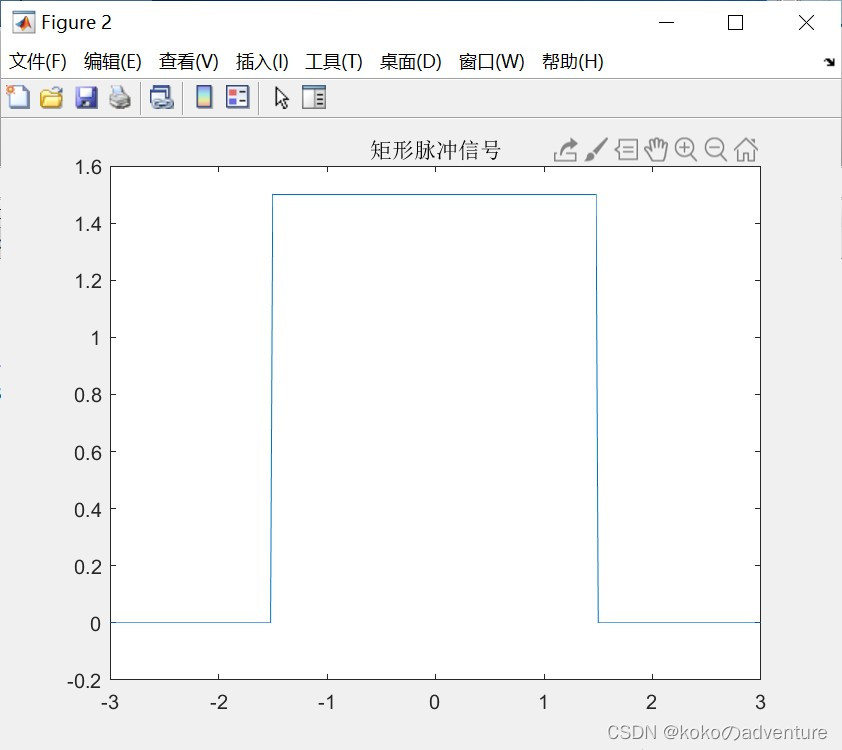
1-1 单位矩形脉冲函数（门函数）

1-2 单位冲激函数（近似）

1-3 三角函数

2 连续时间系统的响应

2-1 单位阶跃响应

​​​​​​​


2-2 单位冲激响应

1 信号的产生

1-1 单位矩形脉冲函数（门函数）

plot函数：plot(x, y) 创建

y

中数据对

x

中对应值的二维线图。​​​​​​​

axis函数：axis( [xmin, xmax, ymin, ymax] ) 设置当前坐标轴x轴和y轴的限制范围。

rectpuls函数：rectpulse(t,w) 可产生高度为1、宽度为w、关于t=0对称的矩形脉冲信号，该函数的横坐标范围由向量t决定，以t=0为中心向左右扩展。

t = -3 : 0.02 : 3;
y1 = 1.5 * rectpuls(t, 3);
plot(t, y1);
title('矩形脉冲信号');
axis([-3, 3, -0.2, 1.6]);

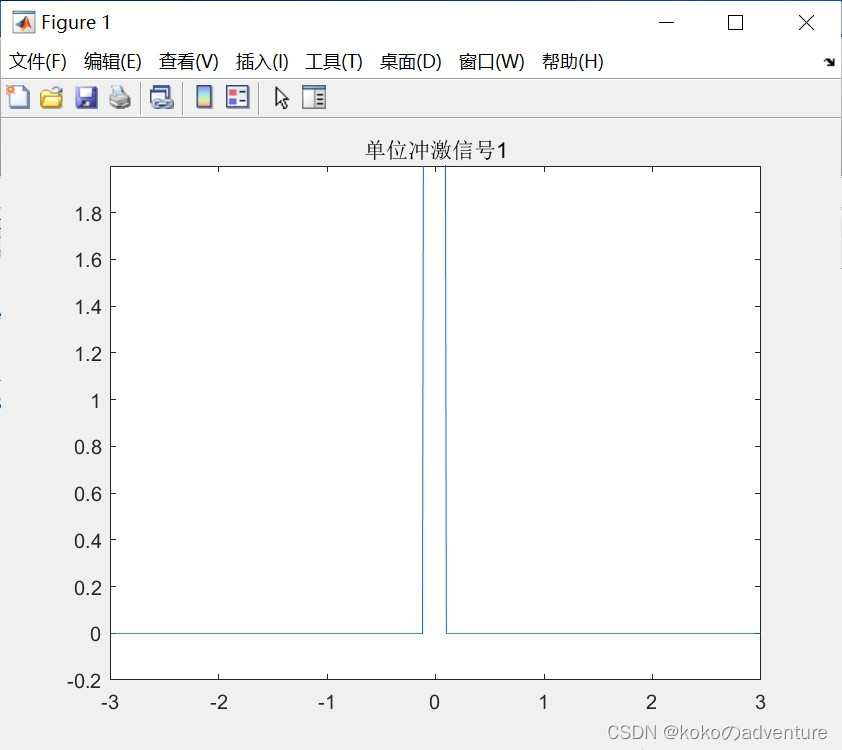
1-2 单位冲激函数（近似）

t = -3 : 0.02 : 3;
y1 = 5 * rectpuls(t, 0.2);
plot(t, y1);
title('单位冲激信号1');
axis([-3, 3, -0.2, 2]);

t = -3 : 0.02 : 3;
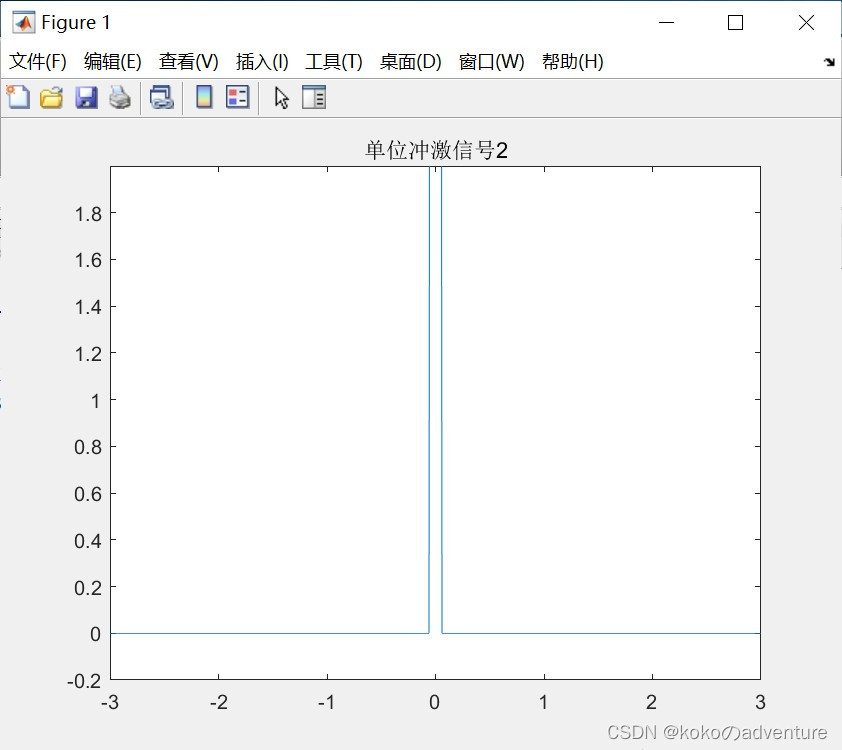
y2 = 10 * rectpuls(t, 0.1);
plot(t, y2);
title('单位冲激信号2');
axis([-3, 3, -0.2, 2]);

1-3 三角函数

A1 = 5;
A2 = 6;
w1 = 12 * pi;
w2 = 18 * pi;
t = 0 : 0.001 : 1;
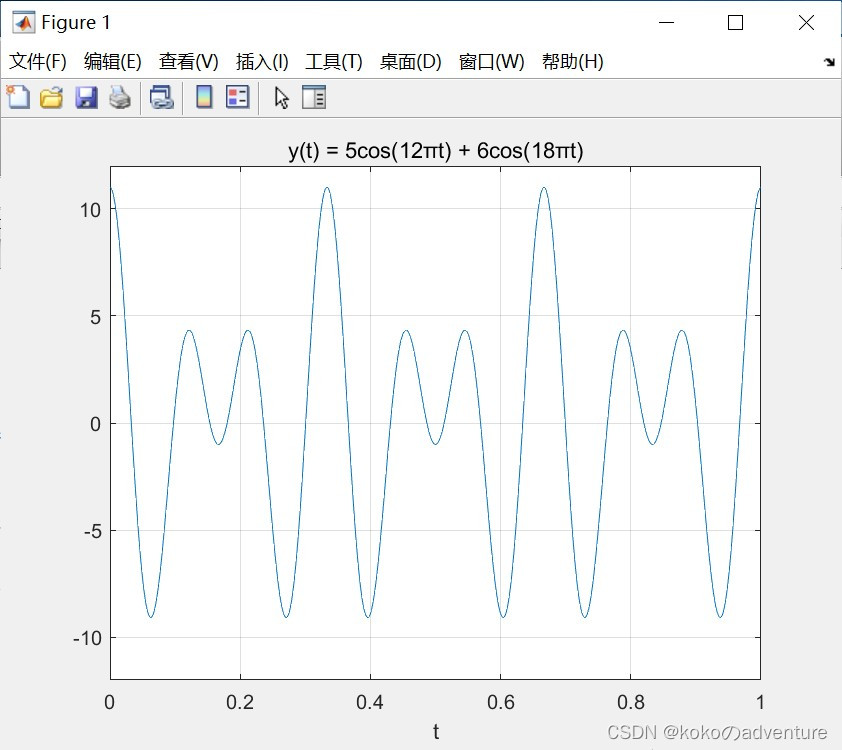
y = A1 * cos(w1 * t) + A2 * cos(w2 * t);
plot(t, y);
grid on;        %绘制网格
title('y(t) = 5cos(12πt) + 6cos(18πt)');
xlabel('t');
axis([0, 1, -12, 12]);

A = 1;
w0 = 2 * pi;
t = 0 : 0.001 : 1;
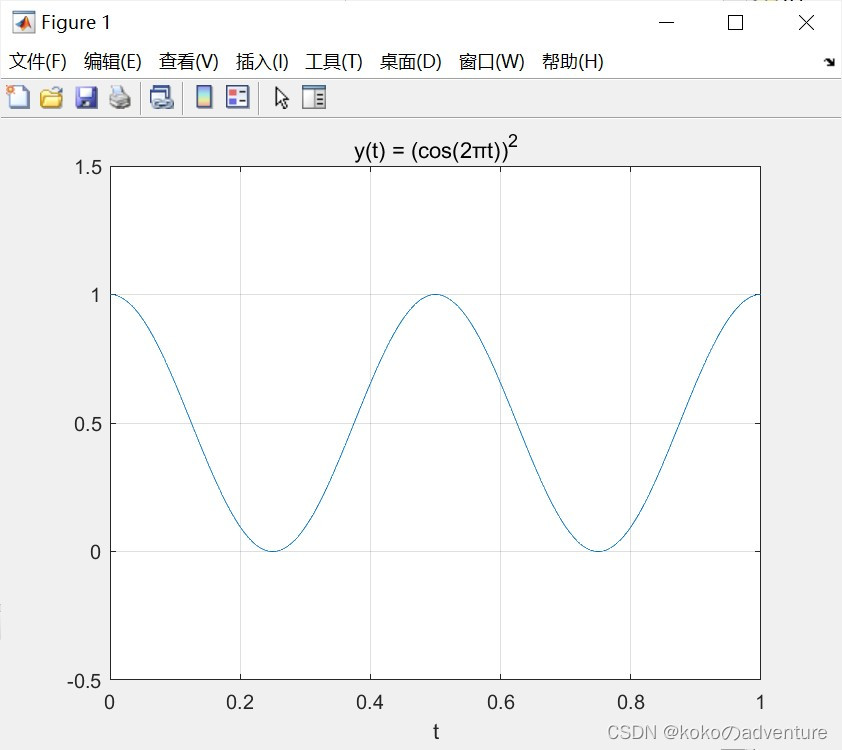
y = A * cos(w0 * t) .* cos(w0 * t);
plot(t, y);
grid on;
title('y(t) = (cos(2πt))^2');
xlabel('t');
axis([0, 1, -0.5, 1.5]);

2 连续时间系统的响应

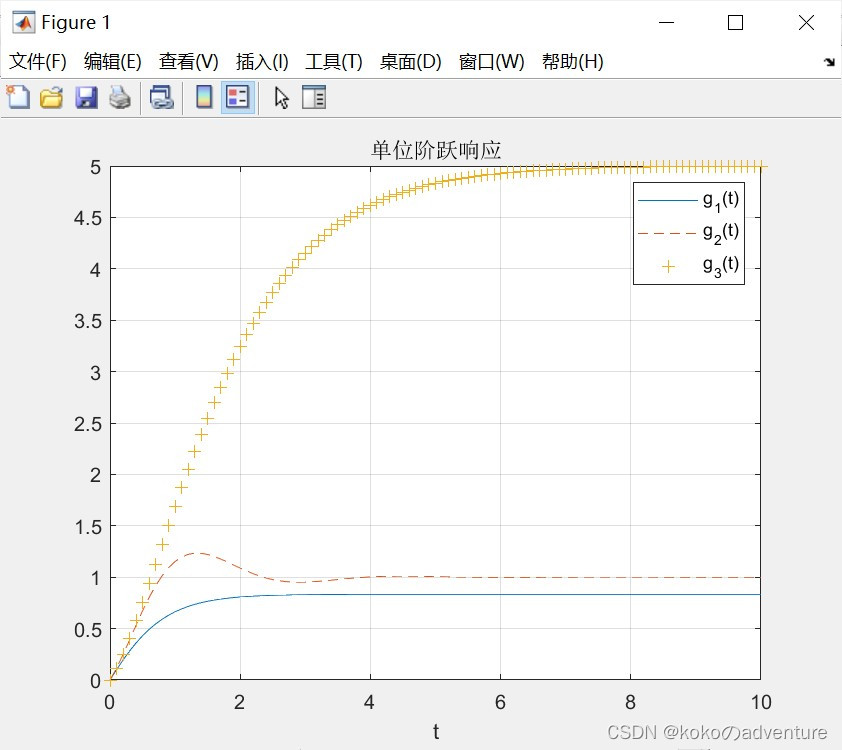
2-1 单位阶跃响应

step函数：

MATLAB中的step()函数_亦散亦聚的博客-CSDN博客_matlab step函数

t = 0 : 0.1 :10;
a = [1 5 6]; b = [1 5]; g1 = step(b, a, t);
a = [1 2 5]; b = [1 5]; g2 = step(b, a, t);
a = [1 2 1]; b = [1 5]; g3 = step(b, a, t);
plot(t, g1, t, g2, '--', t, g3, '+');
xlabel('t');
grid on;
title('单位阶跃响应');
legend('g_1(t)', 'g_2(t)', 'g_3(t)')        %图例

2-2 单位冲激响应

lsim函数：

Matlab中lsim函数使用_jk_101的博客-CSDN博客_lsim

subplot函数：

subplot函数用法（MATLAB)_阳光下的Smiles的博客-CSDN博客_subplot函数怎么用

a = [1 3 2]; b= [-1 2];
sys = tf(b, a);
t = -1 : 0.01 : 5;
h = impulse(sys);       %求数值解

subplot(1, 2, 1);       %在第一块绘图
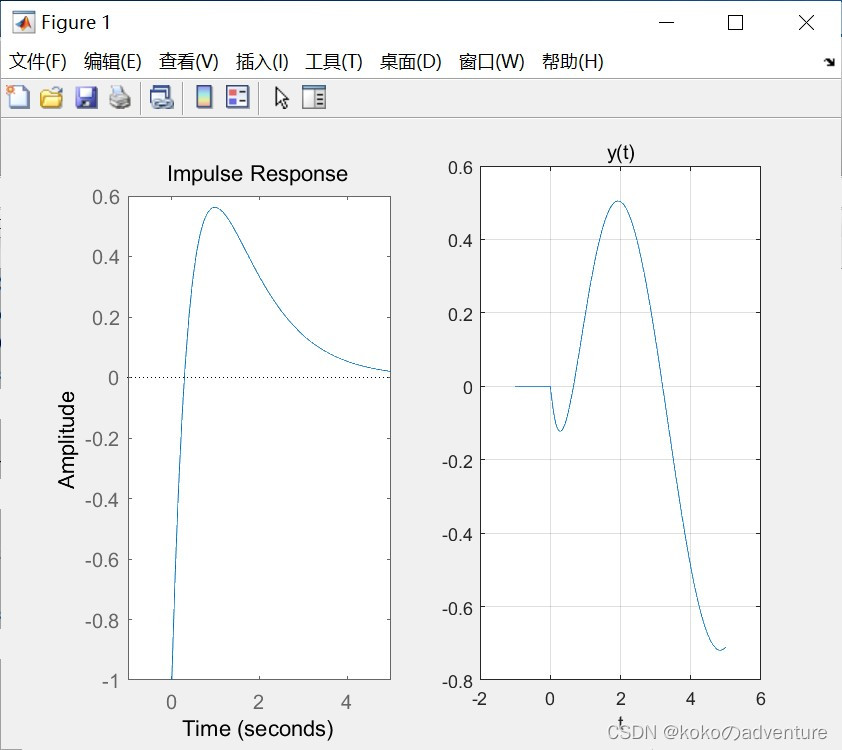
impulse(sys, t);

y1 = (t>0);
y2 = cos(t);
f = y1 .* y2;
y = lsim(sys, f, t);    %求数值解

subplot(1, 2, 2);       %在第二块绘图
lsim(sys, f, t);
plot(t, y);
xlabel('t');
grid on;
title('y(t)');

附一篇博文：

MATLAB：零状态响应(lsim(连续)；filter(离散))、冲激响应(impulse或impz)和阶跃响应(step)、卷积(conv)_FrankStewart的博客-CSDN博客_impulse matlab