个人模板
基础版本(按「秩」(Rank)合并)
#include <vector>
using namespace std;
class Union{
public:
int n;
vector<int> parent;
Union(int _n) {
n = _n;
parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int i) {
if(parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
void _union(int i, int j) {
int rootI = find(i);
int rootJ = find(j);
if(rootI != rootJ) {
if(rootI > rootJ) { // 确保较小的作为根节点
swap(rootI, rootJ);
}
parent[rootJ] = rootI;
}
}
};
优化版本(路径压缩)
#include <vector>
using namespace std;
class Union{
public:
int n;
vector<int> parent;
Union(int _n) {
n = _n;
parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int i) {
if(parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
void _union(int i, int j) {
int rootI = find(i);
int rootJ = find(j);
if(rootI != rootJ) {
if(rootI > rootJ) { // 确保较小的作为根节点
swap(rootI, rootJ);
}
parent[rootJ] = rootI;
}
}
};
例题
547. 省份数量
class Union{
public:
int n;
vector<int> parent;
Union(int _n) {
n = _n;
parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int i) {
int root = i;
while (root != parent[root]) { // 找根节点
root = parent[root];
}
while (i != parent[i]) { // 路径压缩
int temp = parent[i];
parent[i] = root;
i = temp;
}
return root;
}
void _union(int i, int j) {
parent[find(i)] = find(j);
}
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int n = isConnected.size();
Union u(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (isConnected[i][j])
u._union(i,j);
}
}
unordered_set<int> res;
for (int i = 0; i < n; ++i) {
res.insert(u.find(i)); // 注意此处是根节点,而不是单纯的节点
}
return res.size();
}
};
684. 冗余连接
class Union{
public:
int n;
vector<int> parent;
Union(int _n) {
n = _n;
parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int i) {
int root = i;
while (root != parent[root]) { // 找根节点
root = parent[root];
}
while (i != parent[i]) { // 路径压缩
int temp = parent[i];
parent[i] = root;
i = temp;
}
return root;
}
void _union(int i, int j) {
parent[find(i)] = find(j);
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
Union u(n+1);
for (auto edge : edges) {
int a = edge[0], b = edge[1];
if (u.find(a) == u.find(b)) {
return vector<int>{a,b};
} else {
u._union(a,b);
}
}
return vector<int>();
}
};
200. 岛屿数量
(未完成)
737.句子相似性II
(未完成)
给定两个句子 words1, words2 (每个用字符串数组表示),和一个相似单词对的列表 pairs ,判断是否两个句子是相似的。
例如,当相似单词对是 pairs = [[“great”, “fine”], [“acting”,“drama”], [“skills”,“talent”]]的时候,words1 = [“great”, “acting”, “skills”] 和 words2 = [“fine”, “drama”, “talent”] 是相似的。
注意相似关系是 具有 传递性的。
例如,如果 “great” 和 “fine” 是相似的,“fine” 和 “good” 是相似的,则 “great” 和 “good” 是相似的。
而且,相似关系是具有对称性的。
例如,“great” 和 “fine” 是相似的相当于 “fine” 和 “great” 是相似的。
并且,一个单词总是与其自身相似。
例如,句子 words1 = [“great”], words2 = [“great”], pairs = [] 是相似的,尽管没有输入特定的相似单词对。
最后,句子只会在具有相同单词个数的前提下才会相似。
所以一个句子 words1 = [“great”] 永远不可能和句子 words2 = [“doubleplus”,“good”] 相似。
1102. 得分最高的路径
(未完成)
给你一个 R 行 C 列的整数矩阵 A。矩阵上的路径从 [0,0] 开始,在 [R-1,C-1] 结束。
路径沿四个基本方向(上、下、左、右)展开,从一个已访问单元格移动到任一相邻的未访问单元格。
路径的得分是该路径上的 最小 值。例如,路径 8 → 4 → 5 → 9 的值为 4 。
找出所有路径中得分 最高 的那条路径,返回其 得分。
示例 1:
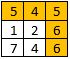
输入:[[5,4,5],[1,2,6],[7,4,6]]
输出:4
解释:
得分最高的路径用黄色突出显示。
示例 2:
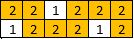
输入:[[2,2,1,2,2,2],[1,2,2,2,1,2]]
输出:2
示例 3:
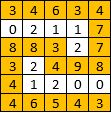
输入:[[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
输出:3
提示:
1 <= R, C <= 100
0 <= A[i][j] <= 10^9
1135. 最低成本联通所有城市
(未完成)
想象一下你是个城市基建规划者,地图上有 N 座城市,它们按以 1 到 N 的次序编号。
给你一些可连接的选项 conections,其中每个选项 conections[i] = [city1, city2, cost] 表示将城市 city1 和城市 city2 连接所要的成本。(连接是双向的,也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连)。
返回使得每对城市间都存在将它们连接在一起的连通路径(可能长度为 1 的)最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务,则请你返回 -1。
示例 1:

输入:N = 3, conections = [[1,2,5],[1,3,6],[2,3,1]]
输出:6
解释:
选出任意 2 条边都可以连接所有城市,我们从中选取成本最小的 2 条。
示例 2:

输入:N = 4, conections = [[1,2,3],[3,4,4]]
输出:-1
解释:
即使连通所有的边,也无法连接所有城市。
提示:
1 <= N <= 10000
1 <= conections.length <= 10000
1 <= conections[i][0], conections[i][1] <= N
0 <= conections[i][2] <= 10^5
conections[i][0] != conections[i][1]
261. 以图判树
(未完成)

1061. 按字典序排列最小的等效字符串
(未完成)

323. 无向图中连通分量的数目
(未完成)
题目描述:
给定编号从
0
到
n-1
的
n
个节点和一个无向边列表(每条边都是一对节点),请编写一个函数来计算无向图中连通分量的数目。
示例:
示例 1:
输入: n = 5 和 edges = [[0, 1], [1, 2], [3, 4]]
0 3
| |
1 --- 2 4
输出: 2
示例 2:
输入: n = 5 和 edges = [[0, 1], [1, 2], [2, 3], [3, 4]]
0 4
| |
1 --- 2 --- 3
输出: 1
注意:
你可以假设在 edges 中不会出现重复的边。而且由于所以的边都是无向边,[0, 1] 与 [1, 0] 相同,所以它们不会同时在 edges 中出现。
924. 尽量减少恶意软件的传播
(未完成)