
- 其中快排的不稳定性出现在:pivot和nums[j]进行交换的时候,比如序列为 5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱;
- 选择排序不稳定性体现在:在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了;
-
堆排序的不稳定性体现在:堆的结构是节点i的孩子为2
i和2
i+1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n /2-1, n/2-2, …1这些个父节点选择元素时,就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1个父节点把后面一个相同的元素没有交换,那么这2个相同的元素之间的稳定性就被破坏了。
排序问题由
Kth Element
问题引出。
LeetCode传送门:
215. 数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
对于
递归问题时间复杂度估算
,粗略贴一张master公式的使用方法

最简单的版本,使用STL当中的
sort
函数,代码如下:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
return nums[nums.size() - k];
}
};
1. 插入排序
插入排序的工作方式非常像人们排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。
插入排序的时间复杂度
O
(
n
2
)
O(n^2)
O
(
n
2
)
,额外空间复杂度
O
(
1
)
O(1)
O
(
1
)
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
void insertSort(vector<int>& arr) {
if (arr.empty() || arr.size() < 2) return;
for (int i = 1; i < arr.size(); ++i) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; --j)
swap(arr, j, j + 1);
}
}
private:
void swap(vector<int>& vec, int idx1, int idx2) {
vec[idx1] = vec[idx1] ^ vec[idx2];
vec[idx2] = vec[idx1] ^ vec[idx2];
vec[idx1] = vec[idx1] ^ vec[idx2];
}
};
2. 归并排序
对于归并排序,相关的问题有:
-
小和问题
:在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和;
解法
:在merge过程中进行比较,注意到进行merge的两个序列均是有序的,所以当一个序列中的某个数小于另一序列时将该数乘以另一序列的剩余元素数,即是该数在数组中所贡献的小和,代码为
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
,另一需要注意的点是,归并所有小和时候,
小和
=
左
侧
归
并
的
小
和
+
右
侧
归
并
小
和
+
左
右
两
侧
数
组
m
e
r
g
e
的
小
和
小和=左侧归并的小和+右侧归并小和+左右两侧数组merge的小和
小
和
=
左
侧
归
并
的
小
和
+
右
侧
归
并
小
和
+
左
右
两
侧
数
组
m
e
r
g
e
的
小
和
,代码为
mergeSort(arr, l, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r)
-
逆序对问题
:在一个数组中,左边的数如果比右边的数大,则折两个数构成一个逆序对,请打印所有逆序对。小和问题的精简版,不再展开。
归并排序的时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O
(
n
l
o
g
n
)
,额外空间复杂度
O
(
n
)
O(n)
O
(
n
)
//归并排序模板
void mergeSort(vector<int>& nums) {
void mergesort(nums, 0, nums.size()-1);
}
void mergesort(vector<int>& nums, int l, int r) {
if(l >= r) return;
int m = l + r >> 1;
mergesort(nums, l, m);
mergesort(nums, m+1, r);
merge(nums, l, m, r);
}
void merge(vector<int>& nums, int l, int m, int r) {
vector<int> helper;
int i = l, j = m + 1;
while(i <= m && j <= r) helper.push_back(nums[i] < nums[j] ? nums[i++] : nums[j++]);
while(i <= m) helper.push_back(nums[i++]);
while(j <= r) helper.push_back(nums[j++]);
for(int i = 0; i < helper.size(); ++i) nums[i + l] = helper[i];
}
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution {
public:
void mergeSort(vector<int>& arr) {
if (arr.empty() || arr.size() < 2) return;
mergeSort(arr, 0, arr.size() - 1);
}
void mergeSort(vector<int>& arr, int l, int r) {
if (l == r) return;
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
private:
void merge(vector<int>& arr, int l, int m, int r) {
vector<int> help;
int i = 0;
int ptr1 = l;
int ptr2 = m + 1;
while (ptr1 <= m && ptr2 <= r)
help.push_back(arr[ptr1] < arr[ptr2] ? arr[ptr1++] : arr[ptr2++]);
while (ptr1 <= m)
help.push_back(arr[ptr1++]);
while (ptr2 <= r)
help.push_back(arr[ptr2++]);
for (int i = 0; i < help.size(); ++i) {
arr[l+i] = help[i];
}
}
};
vector<int> vecGenerator(int size, int min, int max) {
srand((unsigned int)time(NULL));
vector<int> vec;
for (int i = 0; i < size; i++)
vec.push_back(rand() % (max - min) + min);
return vec;
}
void printVector(vector<int>& vec) {
for (vector<int>::iterator iter = vec.begin(); iter != vec.end(); iter++)
cout << *iter << ' ';
cout << endl;
}
int main() {
vector<int> vec = vecGenerator(20, 0, 100);
printVector(vec);
Solution solution;
solution.mergeSort(vec);
printVector(vec);
system("pause");
return EXIT_SUCCESS;
}
3. 堆排序
可见专题讲解:
堆排序(HeapSort)
。
堆排序的时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O
(
n
l
o
g
n
)
,额外空间复杂度
O
(
1
)
O(1)
O
(
1
)
;
建立堆的过程,时间复杂度为
O
(
n
)
O(n)
O
(
n
)
;
堆结构相当重要,也即是优先队列结构,其后的贪心算法几乎都是堆结构实现的(每次都选择当前最优/权重最大的)。
对于
堆结构的数组二叉树实现
,主要有两个操作:
- heapInsert:在数组的最后插入新的元素,并从下至上进行父节点遍历,将新元素置于正确位置;
- heapify:将已是堆结构的数组中的某个元素进行了替换,再将新元素从上至下进行子节点遍历,置于正确位置。
-
其中对于中间的节点其数组下标为idx,则有其父节点下标为
id
x
−
1
2
\frac{idx – 1}{2}
2
i
d
x
−
1
,左子节点下标为
2∗
i
d
x
+
1
2*idx+1
2
∗
i
d
x
+
1
,右子节点下标为
2∗
i
d
x
+
2
2*idx+2
2
∗
i
d
x
+
2
。
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <ctime>
#include <vector>
using namespace std;
class Solution {
public:
void heapSort(vector<int>& arr) {
if (arr.size() < 2 || arr.empty()) return;
for (int i = 0; i < arr.size(); ++i) {
heapInsert(arr, i);
}
int size = arr.size();
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
void heapInsert(vector<int>& arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
void heapify(vector<int>& arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
//int largest = arr[left] > arr[left + 1] && left + 1 < size ? left : left + 1;
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, index, largest);
index = largest;
left = index * 2 + 1;
}
}
void swap(vector<int>& arr, int idx1, int idx2) {
int tmp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = tmp;
}
};
vector<int> vecGenerator(int size, int min, int max) {
srand((unsigned int)time(NULL));
vector<int> vec;
Solution solution;
for (int i = 0; i < size; i++) {
vec.push_back(rand() % (max - min) + min);
}
return vec;
}
void printVector(vector<int>& vec) {
for (vector<int>::iterator iter = vec.begin(); iter != vec.end(); iter++)
cout << *iter << ' ';
cout << endl;
}
int main() {
vector<int> vec = vecGenerator(20, 0, 100);
printVector(vec);
Solution solution;
solution.heapSort(vec);
printVector(vec);
system("pause");
return EXIT_SUCCESS;
}
4. 快速排序
提起快速排序,可以想到其子问题:
荷兰国旗问题
(快排中的partition过程),也即二/三元问题、0-1问题(给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边)。LeetCode传送门:
75. 颜色分类
(给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。)
该问题的解决使用less和more两个下标指针分别记录小于和大于的边界,其中less初始值比处理的数据的边界值小1,more的初始值即为右边界值(考虑到数组的最大下标为长度-1)。进行遍历指针为idx,若是比基准值小,则less+1,将当前值和less+1处数据进行交换,由于所交换的值一定小于基准值,则再将idx+1;若是比基准值大,则more-1,将当前值和more-1处数据进行交换,由于之后的值并没有进行归置,所以idx值不变;重复以上操作直到idx不小于more为止。
时间复杂度为
O
(
n
)
O(n)
O
(
n
)
,额外空间复杂度为
O
(
1
)
O(1)
O
(
1
)
。
class Solution {
public:
void sortColors(vector<int>& nums) {
if(nums.size() == 1 || nums.empty()) return;
int less = -1, left = 0;
int more = nums.size();
while(left < more) {
if(nums[left] < 1) swap(nums, left++, ++less);
else if(nums[left] > 1) swap(nums, left, --more);
else left++;
}
}
private:
void swap(vector<int>& vec, int idx1, int idx2) {
int tmp = vec[idx1];
vec[idx1] = vec[idx2];
vec[idx2] = tmp;
}
};
快速排序的时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O
(
n
l
o
g
n
)
,额外空间复杂度
O
(
l
o
g
n
)
O(logn)
O
(
l
o
g
n
)
//快速排序模板
void quickSort(vector<int>& nums) {
quicksort(nums, 0, nums.size()-1);
}
void quicksort(vector<int>& nums, int l, int r) {
if(l >= r) return;
int i = l - 1, j = r + 1, x = nums[l + r >> 1];
while(i < j) {
do i++; while(nums[i] < x);
do j--; while(nums[j] > x);
if(i < j) swap(nums[i], nums[j]);
}
quicksort(nums, l, j);
quicksort(nums, j+1, r);
}
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution {
public:
void quickSort(vector<int>& arr) {
if (arr.size() < 2 || arr.empty()) {
return;
}
quickSort(arr, 0, arr.size() - 1);
}
void quickSort(vector<int>& arr, int left, int right) {
if(left < right) {
int* p = partition(arr, left, right);
quickSort(arr, left, *p - 1);
quickSort(arr, *(p+1) + 1, right);
}
}
private:
int* partition(vector<int>& arr, int leftIdx, int rightIdx) {
int less = leftIdx - 1;
int more = rightIdx;
while (leftIdx < more) {
if (arr[leftIdx] < arr[rightIdx]) swap(arr, ++less, leftIdx++);
else if (arr[leftIdx] > arr[rightIdx]) swap(arr, --more, leftIdx); //leftIdx右半边的数值仍未进行比较,所以leftIdx不++
else leftIdx++;
}
swap(arr, more, rightIdx); //将基准值归置到正确位置
int* ret = new int[2];
ret[0] = less + 1;
ret[1] = more;
return ret;
}
void swap(vector<int>& arr, int idx1, int idx2) {
int tmp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = tmp;
//arr[idx1] = arr[idx1] ^ arr[idx2];
//arr[idx2] = arr[idx1] ^ arr[idx2];
//arr[idx1] = arr[idx1] ^ arr[idx2];
}
};
vector<int> vecGenerator(int size, int min, int max) {
srand((unsigned int)time(NULL));
vector<int> vec;
for (int i = 0; i < size; i++)
vec.push_back(rand() % (max - min) + min);
return vec;
}
void printVector(vector<int>& vec) {
for (vector<int>::iterator iter = vec.begin(); iter != vec.end(); iter++)
cout << *iter << ' ';
cout << endl;
}
int main() {
vector<int> vec = vecGenerator(20, 0, 100);
printVector(vec);
Solution solution;
solution.quickSort(vec);
printVector(vec);
system("pause");
}
5. 桶排序
非基于比较的排序,与被排序的样本的实际数据状况很有关系,所以实际中并不经常使用。但是桶排序可以实现为稳定的排序。
-
例题
:给定一个数组,求如果排序之后,相邻两数的最大差值,要求时间复杂度O(n),且要求不能用非基于比较的排序。
思路
:多添加一空桶,使得最大差值一定只存在于相邻两桶的情况当中,舍去在同一桶内的情况。
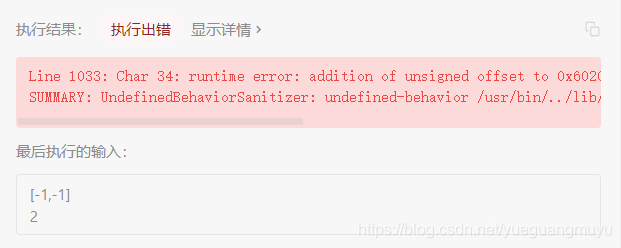
对于桶排序,测试用例当中含有负数测试用例,所以以下代码是以元素均为非负数的数据条件编写的,并不适用。
时间复杂度
O
(
n
)
O(n)
O
(
n
)
,额外空间复杂度
O
(
n
)
O(n)
O
(
n
)
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution {
public:
void bucketSort(vector<int>& arr) {
if (arr.empty() || arr.size() < 2) return;
int max = 0;
for (int i = 0; i < arr.size(); ++i)
max = max > arr[i] ? max : arr[i];
vector<int> bucket(max+1);
for (int i = 0; i < arr.size(); ++i)
bucket[arr[i]]++;
arr.clear();
for (int i = 0; i < max + 1; i++) {
while (bucket[i]-- > 0)
arr.push_back(i);
}
//delete[] bucket;
}
};
vector<int> vecGenerator(int size, int min, int max) {
srand((unsigned int)time(NULL));
vector<int> vec;
Solution solution;
for (int i = 0; i < size; i++) {
vec.push_back(rand() % (max - min) + min);
}
return vec;
}
void printVector(vector<int>& vec) {
for (vector<int>::iterator iter = vec.begin(); iter != vec.end(); iter++)
cout << *iter << ' ';
cout << endl;
}
int main() {
vector<int> vec = vecGenerator(20, 0, 100);
printVector(vec);
Solution solution;
solution.bucketSort(vec);
printVector(vec);
system("pause");
return EXIT_SUCCESS;
}
6. 二分排序
整数二分算法模板 —— 模板题 AcWing 789. 数的范围
#include <iostream>
const int N = 1e5 + 10;
int n, k, q[N];
void binary_search(int q[], int l, int r, int x)
{
while(l < r)
{
int mid = l + r >> 1;
if(q[mid] < x) l = mid + 1;
else r = mid;
}
if(q[l] != x) printf("-1 -1\n");
else printf("%d %d\n", x, l);
return;
}
int main()
{
scanf("%d%d", &n, &k);
for(int i = 0; i < n; ++i) scanf("%d", &q[i]);
for(int i = 0; i < k; ++i)
{
int dest;
scanf("%d", &dest);
binary_search(q, 0, n-1, dest);
}
return 0;
}
7. 排序问题补充
- 归并排序的额外空间复杂度可以变成O(1),但是非常难,不需要掌握,可以搜“归并排序 内部缓存法”;
- 快速排序可以做到稳定性问题,但是非常难,不需要掌握,可以搜“01 stable sort”;
- 有一道题目,是奇数放在数组左边,偶数放在数组右边,还要求原始的相对次序不变。该问题本质为01稳定排序问题,不需要掌握。