1.1编译abs 错误
1 改pcl 1.10 c++14
2、解决方法:将 unsigned int 改为 int 即可
error: call of overloaded ‘abs(unsigned int)’ is ambiguous
121 | unsigned int di = abs(i – src_i);
编译通过
1.2
map –> odom –> base_link –> laser_link
1. 补充代码,实现 gaussian_newton_scanmatcher 模块;(6 分)
(补充代码)
1 InterpMapValueWithDerivatives()函数
Eigen::Vector3d InterpMapValueWithDerivatives(map_t* map,Eigen::Vector2d& coords)
{
Eigen::Vector3d ans;
//TODO
//求出附近左上角最小整数值
int x_0=floor((coords(0)-map->origin_x)/map->resolution+0.5)+map->size_x/2;
int y_0=floor((coords(1)-map->origin_y)/map->resolution+0.5)+map->size_y/2;
//由x1-x0=1,所以u=x-x0,v=y-y0;
//求出离附近整数值差值
double u = (coords(0) - map->origin_x) / map->resolution + 0.5 +double(map->size_x / 2)- (double)x_0 ;
double v = (coords(1) - map->origin_y) / map->resolution + 0.5 + double(map->size_y / 2)- (double)y_0;
//搜索附近分值
double P1,P2,P3,P4;
P1=map->cells[MAP_INDEX(map,x_0,y_0)].score;
P2=map->cells[MAP_INDEX(map,x_0+1,y_0)].score;
P3=map->cells[MAP_INDEX(map,x_0+1,y_0+1)].score;
P4=map->cells[MAP_INDEX(map,x_0,y_0+1)].score;
//插值计算分值
//M(ST)
ans(0) = v*(u*P3+(1-u)*P4)+(1-v)*(u*P2+(1-u)*P1);
//对函数进行x和y求导
//STdx
ans(1)=(v*(P3-P4) + (1-v)*(P2-P1))/map->resolution;
//STdy
ans(2)=( u*(P3-P2) + (1-u)*(P4 - P1) )/map->resolution;
//END OF TODO
return ans;
}2 ComputeHessianAndb()函数
double ComputeHessianAndb(map_t* map, Eigen::Vector3d now_pose,
std::vector<Eigen::Vector2d>& laser_pts,
Eigen::Matrix3d& H, Eigen::Vector3d& b)
{
H = Eigen::Matrix3d::Zero();
b = Eigen::Vector3d::Zero();
//TODO
Eigen::Matrix3d T;
T<<cos(now_pose(2)),-sin(now_pose(2)),now_pose(0),
sin(now_pose(2)),cos(now_pose(2)),now_pose(1),
0,0,1;
Eigen::Vector3d laser_pose;
Eigen::Vector3d ST3d;
Eigen::Vector2d ST2d;
Eigen::Vector3d ans;
Eigen::Vector2d coords ;
Eigen::Vector2d dMst ;
Eigen::Matrix<double,2,3>dST;
double error=0.0;
for(int i=0;i<laser_pts.size();i++)
{
laser_pose<<laser_pts[i][0],laser_pts[i][1],1;
//M(S(T)) 计算
ST3d=T*laser_pose;
ST2d <<ST3d(0),ST3d(1);
ans=InterpMapValueWithDerivatives(map,ST2d);
//dst
dMst << ans(1), ans(2);
double J1 = ans(1) ; double J2 = ans(2);
double J3 = ans(1)*dST(0,2)+dST(1,2)*ans(2);
H(0,0) += J1*J1; H(0,1) += J1*J2; H(0,2) += J3*J1;
H(1,0) += H(0,1); H(1,1) += J2*J2; H(1,2) += J3*J2;
H(2,0) += H(0,2) ; H(2,1) += H(1,2) ; H(2,2) +=J3*J3;
double er = 1-ans(0);
Eigen::Vector3d ver;
ver << J1*er,J2*er,J3*er;
b += ver;
error += er*er;
}
return error*0.5;
//END OF TODO
}3 GaussianNewtonOptimization()函数
void GaussianNewtonOptimization(map_t*map,Eigen::Vector3d& init_pose,std::vector<Eigen::Vector2d>& laser_pts)
{
int maxIteration = 20;
double lasrterror =0;
Eigen::Vector3d now_pose = init_pose;
bool flat=true;
Eigen::Vector3d DT;
static Eigen::Vector3d DT_sum;
for(int i = 0; i < maxIteration;i++)
{
//TODO
Eigen::Matrix3d H;
Eigen::Vector3d b;
double error=ComputeHessianAndb(map,now_pose,laser_pts,H,b);
Eigen::Vector3d dT=H.ldlt().solve(b);
if( lasrterror > 0 && error > lasrterror)//分值越大,函数结果越小
{
break;
}
if(std::isnan(dT[0]))
{
std::cout<<"result is nan!"<<std::endl;
break;
}
lasrterror = error;
DT += dT;
now_pose += dT;
//END OF TODO
if(error <10e-5)
break;
//END OF TODO
}
init_pose = now_pose;
}
运行说明:
source 之后用 rosrun gaussian_newton_scanmatcher gaussian_newton_node 命令运行。播放
bag 包,之后可用 rviz 查看轨迹。
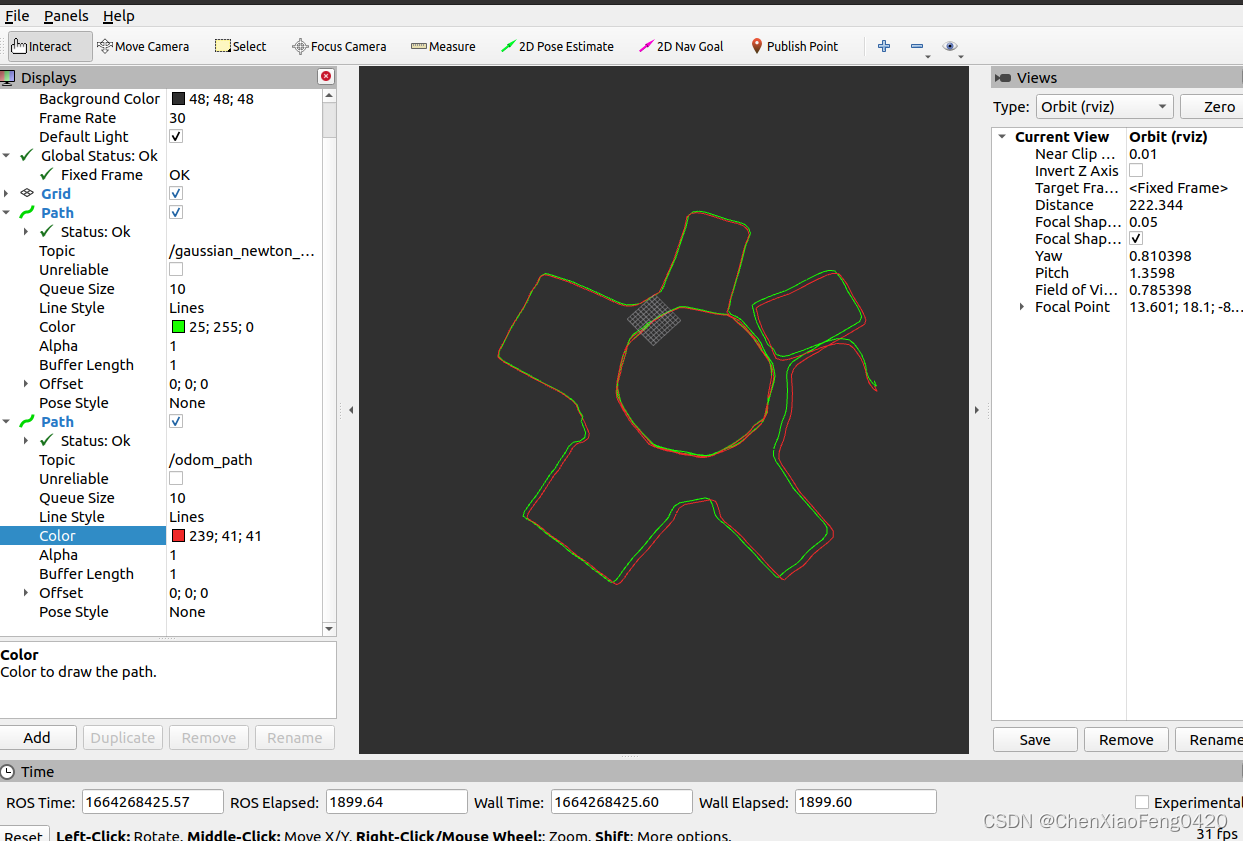
2. 简答题,开放性答案:提出一种能提升第一题激光匹配轨迹精度的方法,并解释原因;(2 分)
3. 阅读论文 The Normal Distributions Transform: A New Approach to Laser Scan Matching,
回答以下问题:(2 分)
(1) NDT 的优化函数(score)是什么?
(2) 简述 NDT 根据 score 函数进行优化求解的过程。

4. 机器人在 XY 方向上进行 CSM 匹配。下图左为机器人在目标区域粗分辨率下 4 个位置的匹配得分,得分越高说明机器人在该位置匹配的越好,下图右为机器人在同一块地图细分辨率下每个位置的匹配得分(右图左上 4 个小格对应左图左上一个大格,其它同理)。如果利用分枝定界方法获取最终细分辨率下机器人的最佳匹配位置,请简述匹配和剪枝流程

4-1—遍历粗分辨率下 4 个位置, best_score=-无穷,第一次选取左图最大的 99 分粗分辨率节点;
4-2—对 99 分粗分辨率节点进行分枝,进入细分辨率节点,此时为叶子节点,遍历后选取最大的 87 分的
细分辨率节点,best_score=87;
4-3—返回粗分辨率节点,第一个节点是 85 分,小于 best_score=87 ,进行剪枝;
4-4—在粗分辨率节点继续查找,循环到第三节点 98 分,大于 best_score=87,进入细分辨率节点,此
时为叶子节点,遍历后得到 95 分节点大于 best_socre=87,则 bust_score=95;
4-5—返回粗分辨率节点继续查找,循环到第四节点 96 分,大于 beat_score=95 ,进入细分辨率节点,
遍历后所有叶子节点都小于 best_score=95,返回粗分辨率节点,粗分辨率节点为空,结束