之前的代码后面发现是有bug的,之前在sgbm算法经过考验下来还是有bug,
花了点时间搞懂原理,网上的东西很多有误导性或者自己没完全明白,
还是按自己的思路来,
我把仿真的工程放到github上,大家可以下载下来调试,
https://github.com/tishi43/div
增加了注释,非pipeline版本的除法代码,
// 原理就是小学时代的除法算式原理,
// 1284除以15,1284一位一位给,
// step 1: 先给1,与15比,比15小,所以最高位的结果是0,1除以15的余数是1,拖下来,
// step 2: 再给1位,那就是12,12和15比,还是比15小,这位的结果也是0,12除以15的余数是12,拖下来,
// step 3: 再给1位,那就是128,比15大了,是15的8倍多,这位结果是8,余数是8,
// step 4: 再给1位,就是4,加上前面的余数8为84,84是15的5倍多,这位结果是5,余数9为最后的余数
// Done, 被除数是几位,就需要几个step
//step 1:
// 0
// /--------
// 15 \/ 1 2 8 4
// 0
// --------
// 1
//step 2:
// 0 0
// /--------
// 15 \/ 1 2 8 4
// 0
// --------
// 1 2
// 0
// --------
// 1 2
//step 3:
// 0 0 8
// /--------
// 15 \/ 1 2 8 4
// 0
// --------
// 1 2
// 0
// --------
// 1 2 8
// 1 2 0
// -------
// 8
//step 4:
// 0 0 8 5
// /--------
// 15 \/ 1 2 8 4
// 0
// --------
// 1 2
// 0
// --------
// 1 2 8
// 1 2 0
// -------
// 8 4
// 7 5
// -----
// 9
//上面的例子是按10进制的1位1位给,推广到二进制,以142/10为例
//step 1~4省略,被除数给出4位,也就是1000,还是比1010小,高4位的结果是0000
//step 5,被除数给到5位,10001比除数1010大了,这个step的结果是1,
//与10进制相比,结果只有0,1之分,大于等于,结果就是1,小于,结果就是0
// 00001
// /---------
// 1010 \/ 10001110
// 1010
// ------
// 111
//step 6,前一步的余数111,再加上新拖下来新的1位1,就是1111,比1010大,结果是1
// 000011
// /---------
// 1010 \/ 10001110
// 1010
// ------
// 1111
// 1010
// ----
// 101
//step 7,前一步的余数101,再加上新拖下来新的1位1,就是1011,比1010大,结果是1
// 0000111
// /---------
// 1010 \/ 10001110
// 1010
// ------
// 1111
// 1010
// -----
// 1011
// 1010
// -----
// 1
//step 8,前一步的余数1,再加上拖下来新的1位0,就是10,比1010小,结果是0
// 00001110
// /---------
// 1010 \/ 10001110
// 1010
// ------
// 1111
// 1010
// -----
// 1011
// 1010
// -----
// 10
//Done,结果是1110,余数10
//rst : div_result= 0000_1 0001110
// ------ 这5bit和1010比,相当于被除数先给最前的1,比1010小,然后div_result<<1
//cycle 1: div_result= 00010 001110 0
//...
//cycle 4: div_result= 10001 110 0000
// ----- 这5bit和1010比,大于了,下一步为({10001-1010余数,111 0000}<<1)|1即({00111,111000}<<1)|1,
// 第0bit用来存结果了,或1就是存结果1,而div_result<<1,相当于存结果0
//cycle 5: div_result= 01111 1000001
// ----- 这5bit比1010大,
//cycle 6: div_result= 01011 0000011
// ----- 这5bit比1010大,
//cycle 7: div_result= 00010 0000111
// ----- 这5bit比1010小
//cycle 8: div_result= 0010 00001110
// ----4bit余数 --------8bit结果
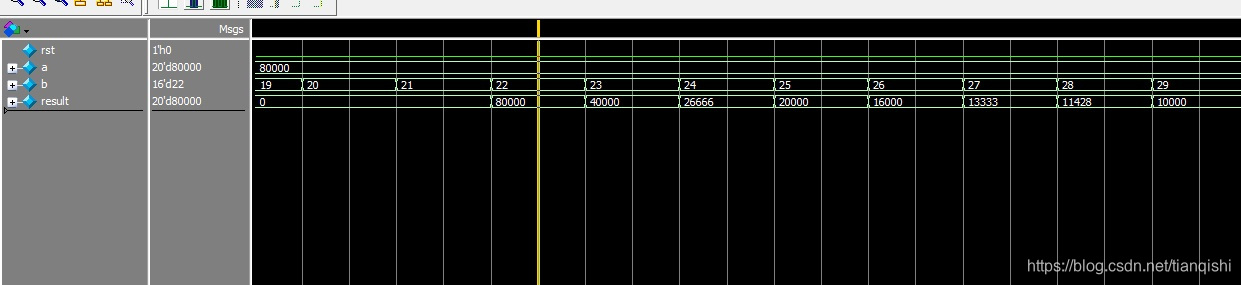
module div_by_shift_sum #(
parameter WidthD0=64,
parameter WidthD1=32,
parameter WidthQ=WidthD0+WidthD1)
(
input wire clk,
input wire rst,
input wire [WidthD0-1:0] a,
input wire [WidthD1-1:0] b,
output wire [WidthD0-1:0] result,
output reg valid
);
localparam CountBits = $clog2(WidthD0-1)+1;
reg [WidthQ-1:0] div_result;
reg [WidthD1 :0] div_sub_val; //每步的余数
reg [CountBits-1:0] counter;
always @ (posedge clk) begin
if (rst) begin
div_result <= {{WidthD1{1'b0}}, a};
counter <= 0;
valid <= 0;
end
else if (~valid)begin
if (div_result[WidthQ-1:WidthD0-1]>=b)
div_result <= ({div_sub_val,div_result[WidthD0-2:0]} << 1) | 1;
else
div_result <= div_result << 1;
counter <= counter+1;
if (counter==WidthD0-1)
valid <= 1;
end
end
integer ii;
always @(*) begin
div_sub_val = div_result[WidthQ-1:WidthD0-1]-b;
end
assign result = div_result[WidthD0-1:0];
endmodule
module div_by_shift_sum_pipeline #(
parameter WidthD0=64,
parameter WidthD1=32,
parameter WidthQ=WidthD0+WidthD1)
(
input wire clk,
input wire [WidthD0-1:0] a,
input wire [WidthD1-1:0] b,
output wire [WidthD0-1:0] result
);
reg [WidthD1-1:0] b_d[0:WidthD0];
reg [WidthQ-1:0] div_result_d[0:WidthD0];
reg [WidthD1 :0] div_sub_val[0:WidthD0];
always @ (posedge clk) begin
b_d[0] <= b;
div_result_d[0] <= {{WidthD1{1'b0}}, a};
end
integer ii;
always @(*) begin
for (ii = 0; ii <= WidthD0; ii = ii + 1) begin
div_sub_val[ii] = div_result_d[ii][WidthQ-1:WidthD0-1]-b_d[ii];
end
end
always @(posedge clk) begin
for (ii = 1; ii <= WidthD0; ii = ii + 1) begin
if (div_result_d[ii-1][WidthQ-1:WidthD0-1]>=b_d[ii-1])
div_result_d[ii] <= ({div_sub_val[ii-1],div_result_d[ii-1][WidthD0-2:0]} << 1) | 1;
else
div_result_d[ii] <= div_result_d[ii-1] << 1;
b_d[ii] <= b_d[ii-1];
end
end
assign result = div_result_d[WidthD0][WidthD0-1:0];
endmodule
版权声明:本文为tianqishi原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。