博客

RVEA：参考向量引导多目标优化进化算法

参考文献

《A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization》

要点

• 本文提出了一种参考向量引导多目标优化进化算法。参考向量不仅可以用于将原始的多目标优化问题分解为多个单目标子问题，而且可以阐明用户偏好，以针对整个Pareto前沿的首选子集作为目标。
• 在提出的算法中，采用了一种称为角度惩罚距离的标量化方法来平衡高维目标空间中解的收敛性和多样性。提出了一种自适应策略，根据目标函数的尺度动态调整参考向量的分布。

一、介绍

本文的主要贡献如下：

• 一种标量化方法，称为角度惩罚距离（APD），旨在根据目标数和世代数在多目标优化中动态平衡收敛和多样性。在提出的APD中，收敛标准是通过候选解与理想点之间的距离来衡量的，而多样性准则是通过候选解与参考向量之间的锐角来衡量的。注意，如果参考向量用于表示用户偏好，则该角度还指示用户偏好的满意度。
• 提出了一种自适应策略来调整参考向量，以处理未很好归一化的目标函数。自适应策略根据不同目标函数的范围来调整参考向量的分布，以确保即使目标函数没有很好地归一化或PF的几何结构高度不对称，候选解也可以在目标空间中均匀分布是高度不对称的。该策略主要用于获得均匀分布的帕累托最优子集。
• 结果表明，参考向量还可以提供一种高效的和计算有效的方法来表达偏好。这种偏好表达在多目标优化中特别有价值，因为在这种情况下很难获得整个PF的代表性近似值。通过指定中心向量和半径，我们提出了一种基于参考向量的偏好表达方法，该方法能够在目标空间的偏好区域中生成均匀分布的帕累托最优解。
• 问了提高RVEA在不规则PF问题的性能，提出了一种参考向量再生成策略。基本思想是使用额外的参考向量集在目标空间中进行探索，以便提高由RVEA获得的具有不规则PF问题的解的密度。

二、背景

参考向量

在不失一般性的前提下，本文中使用的所有参考向量均为第一象限内的单位向量，其原点为起始点。从理论上讲，这样的单位向量可以通过将任意向量除以其范数轻松生成。但是，实际上，对于目标空间的均匀分布的覆盖范围，需要均匀分布的单位参考向量。为了产生均匀分布的参考向量，我们采用[A multiobjective evolutionary algorithm using Gaussian process-based inverse modeling]中介绍的方法。首先，使用规范的单纯形格设计方法在单元超平面上生成一组均匀分布的点。

其中i = 1，…，N，其中N为均匀分布点的数量，M为目标数，H为单纯形格设计的正整数。然后，通过变换可以得到相应的单位参考向量vi。

该图将参考点从一个超平面映射到一个超球面，其示例如图所示。根据单纯形晶格设计的性质，给定H和M，总数为N =(H + M-1, M-1)个均匀分布的参考向量。

单纯形格

给定两个向量v1和v2，两个向量之间的锐角θ的余弦值可用于测量它们之间的空间关系，其计算公式为

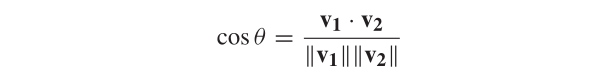
||·||计算范数，表示向量长度。

三、提议的RVEA

主框架

A、子代生成

• 采用模拟二项交叉（SBX）和多项式突变来创建子代种群。
• 没有用任何明确的交配选择策略。N个个体中每个个体都有相同的概率参与繁殖过程。
• 参考向量选择策略可以有效地管理目标空间的小子空间内的收敛性和多样性，从而使每个子空间内的个体都可以对总体做出同样的贡献。

B、参考向量引导选择

RVEA使用参考向量将目标空间划分为多个子空间，并且在每个子空间内分别执行选择。

参考向量引导选择包括四个步骤：

• 目标值转换
• 种群划分
• APD计算
• 精英选择

a)目标值转换

本文中的参考向量的起始点始终是坐标原点，将种群Pt中的个体的目标值F(t)={f(t1), f(t2), …, f(t|Pt|)}转换为F’(t)，通过以下方法：

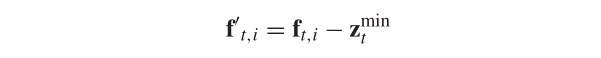
其中zmin(t)=(zmin(t, 1), zmin(t, 2), …, zmin(t, m))表示根据F(t)计算的最小目标值。

转换操作的作用是：

• 确保转换后的目标值都在第一象限内，其中每个目标函数的极点在相应的坐标轴上，从而最大程度地覆盖了参考向量。
• 将理想点设置为坐标系原点。

b)种群划分

目标值转换后，通过将每个个体与其最近的参考向量相关联，将种群Pt划分为N个子种群。

如图，两个向量的空间关系通过两个向量之间的锐角来测量

即目标向量和参考向量之间的余弦值可以计算为：

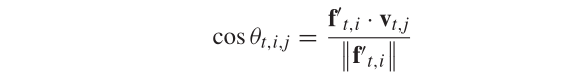
子种群划分

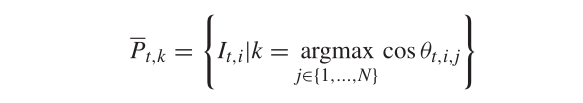
C、APD距离

一旦将种群Pt划分为N个子种Pt1，Pt2，…，PtN，就可以从每个子种群中选择一位精英，为下一代创建Pt+1。

由于我们的动机是在最接近理想点的每个参考向量上找到解，因此选择标准包括两个子条件，即对于候选解相关联的参考向量而言，收敛标准和多样性标准。

用||f’||衡量收敛性标准，用θ衡量多样性标准，为了平衡两者之间的关系，APD距离定义为：

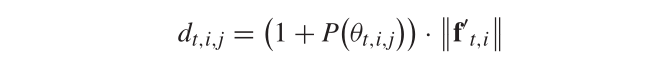
P是一个关于θ的惩罚函数

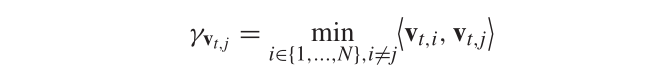
α是用户自定义参数，γ是与vtj形成夹角最小的其他参考向量的角度。

一般情况下，多目标优化早期强调收敛性，后期更着重多样性。

惩罚函数就是基于这个问题设计的，早期t<<tmax，所以P≈0，意味着d≈||f’||，||f’||强调收敛性，后期t逐渐增大，P的影响也随之递增，以达到后期强调多样性的目的。

角度γ用于归一化由vtj指定的子空间中的角度，当某些参考向量的分布过于密集（或过于稀疏），从而导致候选解与参考向量之间的角度极小（或很大）时，此角度归一化过程特别有意义。

与NSGA-III中所提出的角度归一化方法有两个主要区别：1）归一化角度（而不是目标）将不会改变目标的实际位置。2）在每个子空间内独立进行的角度归一化不会影响其他子空间中候选解的分布。

另外，由于候选解的分布的稀疏度直接关系到目标空间的维数，即M的值，所以惩罚函数P也与M有关，以进行自适应调整罚函数值的范围。

参考向量选择策略伪代码如下

D、参考向量适应

给定一组均匀分布的单位参考向量，只有所有目标值都归一化到相同范围，如[0, 1]时才会发生图(a)中的情况，而实际上可能存在将目标值缩放到不同范围的情况，此时，如果还用均匀分布的参考向量，就会发生图(b)的情况，产生了不均匀的解。

解决上述问题的一种直观方法是随着搜索的进行动态地进行目标归一化。然而不适合RVEA，因为会改变目标值。

RVEA按照以下方法根据目标值的范围调整参考向量：

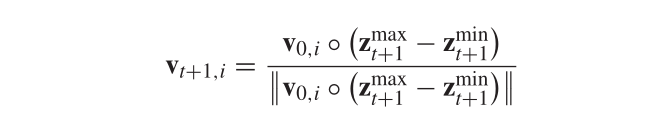
z是目标值。表示在某目标下极值之差。参考向量适应策略如下