3.单位矩阵,逆矩阵
修改于
2020年10月01日
问题或建议,请留言!
目录
词汇单位矩阵eye()逆矩阵定义及性质代码画图检验
词汇
-
identity matrix 单位矩阵
-
the inverse of a matrix 逆矩阵
使用逆矩阵解线性方程组
单位矩阵
单位矩阵
是一个维度为n*n的
方阵
,对角线(diagonal)上的元素为1,其余为0。
一个单位矩阵的特殊之处在于矩阵乘上它不会改变。从这个意义上讲,它与实数中的数字1相似。

eye()
1import numpy as np
2A = np.eye(3)
3print(A)
the space doesn’t change when we
apply
the identity matrix to it.
逆矩阵
定义及性质
方阵(n x n)
,ad-bc 叫做A的行列式(determinant),记为det A
,
A
可逆(
invertible,非奇异(nonsingular)
),逆矩阵
,
A
不可逆
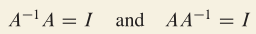
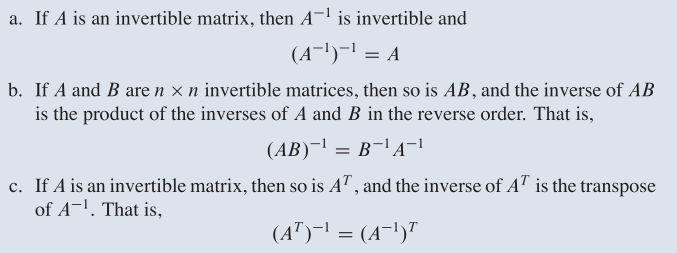
解
可得
只要求A的逆矩阵就好了
例
矩阵形式下,我们的方程变为
代码
1import numpy as np
2A = np.array([[2, -1],
3 [1, 1]])
4# lin:linear alg:algebra
5A_inv = np.linalg.inv(A)
6b = np.array([[0],
7 [3]])
8x = A_inv.dot(b)解得
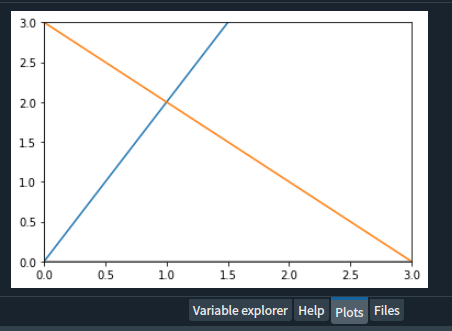
这意味着点(1,2)为我们的解,也是两条方程的交点。
画图检验
1import numpy as np
2import matplotlib.pyplot as plt
3#-10 -> 10 不含10
4x = np.arange(-10, 10)
5y = 2*x
6y1 = -x + 3
7plt.figure(num="figure")
8plt.plot(x, y)
9plt.plot(x, y1)
10plt.xlim(0, 3)#设置x轴刻度范围
11plt.ylim(0, 3)
12# draw axes
13# 画出竖线 ,vertical
14plt.axvline(x=0, color='grey')
15# 画出横线 ,horizontal
16plt.axhline(y=0, color='grey')
17plt.show()
18plt.close()