博客

题目传送门

给定n*n的矩阵A，求A^k

输入格式

第一行，n,k

第2至n+1行，每行n个数，第i+1行第j个数表示矩阵第i行第j列的元素

输出格式

输出A^k

共n行，每行n个数，第i行第j个数表示矩阵第i行第j列的元素，每个元素模10^9+7

输入

2 1

1 1

1 1

输出

1 1

1 1

矩阵相乘原理：

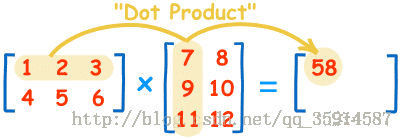
递推式， 例：

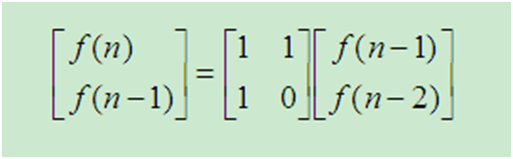
矩阵可以这样记：f（n-1）的下一项为f(n）；f(n-2）的下一项为 f(n-1) ; 矩阵中是赋值1还是0，取决于如何让相乘后的矩阵等于左边的矩阵；

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <sstream>
#include <cmath>
#define ll long long 
#define ull unsigned long long 

using namespace std;

const ll maxn=500005;
const ll INF=0x3f3f3f;
const ll mod=1e9+7;
const ll MAX=1e7+10;

ll n,p;

struct Mat
{
	ll m[101][101];
	
};

Mat a,e;	//a为原矩阵，e为单位矩阵；


inline Mat mul(Mat x,Mat y)			//重载乘法运算符；
{
	 Mat c;
	 
	 for(int i=1;i<=n;i++)
	   for(int j=1;j<=n;j++)
	     c.m[i][j]=0;			//初始化清空；
	
	for(int i=1;i<=n;i++)
	 for(int j=1;j<=n;j++)
	  for(int k=1;k<=n;k++)
	    {
	    	c.m[i][j]=c.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod;		//矩阵相乘（有固定规则，如上图）；
	    	c.m[i][j]%=mod;
	    }
	    
	return c;
	
}


inline Mat quickmod(Mat x,ll y)		//矩阵快速幂（和常规快速幂基本相同，只不过要重载一下运算符）；
{
	for(int i=1;i<=n;i++)	
	  	e.m[i][i]=1;		//初始化单位矩阵（主对角线上为1，其余为0）；

	 Mat ans=e;		//矩阵可直接赋值；
	
	 while(y)
	 {
	 	 if(y&1)
	 	   ans=mul(ans,x);	//相乘；
	 	   
	 	 x=mul(x,x);	
	 	 
	 	 y>>=1;
	 	
	 }
	
	return ans;
}


int main()
{
	scanf("%lld %lld",&n,&p);	
	
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=n;j++)
	  	scanf("%lld",&a.m[i][j]);	//输入原矩阵；
	  
	  
	Mat ans=quickmod(a,p);	//矩阵快速幂；
	
	for(int i=1;i<=n;i++){		//输出相乘后的矩阵；		
		for(int j=1;j<=n;j++)
		  printf("%lld ",ans.m[i][j]%mod);
		  
		printf("\n");
	}
	
	
	
		 
	return 0;
}