在基于图像的视觉伺服(IBVS)中的图像雅可比矩阵的学习和理解
主要参考了这两篇论文中有关IBVS中的内容,有刚入门视觉伺服研究的小伙伴们可以去看看这两篇论文:
1、Chaumette F, Hutchinson S. Visual servo control. I. Basic approaches[J]. IEEE Robotics & Automation Magazine, 2006, 13(4): 82-90.
2、Hutchinson S, Hager G D, Corke P I. A tutorial on visual servo control[J]. IEEE transactions on robotics and automation, 1996, 12(5): 651-670.
一、第一篇论文:Visual Servo Control Part I: Basic Approaches
一个点在相机坐标系下的3D点坐标为:
X
=
(
X
,
Y
,
Z
)
\textbf{X}=(X,Y,Z)
X
=
(
X
,
Y
,
Z
)
,
其在图像坐标系下的2D坐标为:
x
=
(
x
,
y
)
\textbf{x}=(x,y)
x
=
(
x
,
y
)
根据相机透视模型(论文A Tutorial on Visual Servo Control中的图):

(Note:坐标表达字母不同)
[
x
y
]
=
f
Z
[
X
Y
]
(
1
)
\begin{bmatrix} x \\ y\end{bmatrix}=\frac{f}{Z} \begin{bmatrix} X\\Y \end{bmatrix} (1)
[
x
y
]
=
Z
f
[
X
Y
]
(
1
)
f是焦距。这个式子就将图像坐标系与相机坐标系下的点联系了起来。那如何将图像点的移动速度与相机的移动速度联系起来呢?就需要以下两步:
1、当一个3D点固定不动的时候,相机移动了,那3D点也会相对的移动。此处讨论的是eye-in-hand方式,相机的移动速度也就是末端执行机构的移动速度为
[
ω
x
ω
y
ω
z
v
x
v
y
v
z
]
T
\begin{bmatrix} \omega_x &\omega_y &\omega_z &v_x &v_y &v_z\end{bmatrix}^T
[
ω
x
ω
y
ω
z
v
x
v
y
v
z
]
T
,那么就可以根据下面的式子计算3D点的移动速度:
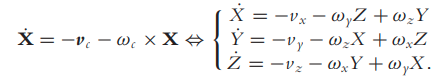
2、(这个式子可以这样理解:x方向上的角速度会引起y和z方向上的速度),由相机的移动速度就得到了3D点的移动速度,再将式(1)代入到式子中就得到了相机的移动速度与2D点的移动速度的关系:(这里默认f=1了)
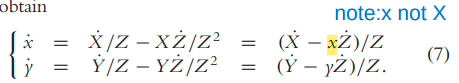
代入得到:

二、在这篇论文中A Tutorial on Visual Servo Control
2D坐标为:
(
u
,
v
)
(u,v)
(
u
,
v
)
,3D点坐标为:
(
x
,
y
,
z
)
(x,y,z)
(
x
,
y
,
z
)
,与上述表达的字母不同,可以看上面的相机同透视模型图。
在第V部分的基于图像的视觉伺服讲解中,B部分是eye-to-hand方式,相机被固定在一个位置,点P为末端执行机构上的一个点,P在相机坐标系下的移动速度也就是末端执行机构在相机坐标系下的移动速度为:
[
ω
x
ω
y
ω
z
T
x
T
y
T
z
]
T
\begin{bmatrix} \omega_x &\omega_y &\omega_z &T_x &T_y &T_z\end{bmatrix}^T
[
ω
x
ω
y
ω
z
T
x
T
y
T
z
]
T
,根据下面的式子求P点在x,y,z方向上的速度,因为这里是P点动,相机固定;而上面那篇论文是相机动,3D点固定,所以下面的这个式子跟上面论文中的式子正负号是相反的 。并且这里将焦距代入了进来。但计算的流程都是一样的:
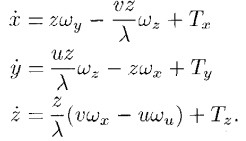
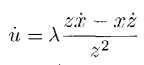
得到平面点的速度与点在相机坐标系下的速度之间的相对关系:
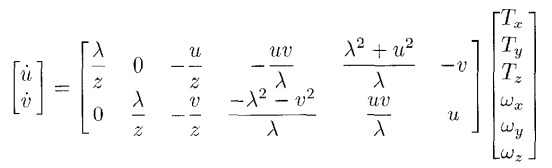
经过这两篇论文的学习,到这里,我们的图像雅可比矩阵就完全明白了。