求解一个数的某一次方根,对于某些特殊的数字的特殊次方根而言,我们可以口头进行计算;但是通常情况下,我们都只能借助适当的数学工具来进行计算。本次就是基于Python中求解一个数的n次方根的方法的学习总结。
1、利用Python中的内置函数(pow函数)求解
Python中的pow函数一般有两种形式:pow(x,y)与pow(x,y,z);其中pow(x,y)表示x的y次方的值,pow(x,y,z)则表示x的y次方除以z的余数。
具体代码如下:
#导入必要的库
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import math
from sympy import *
#利用pow函数计算2020的15次方根与演示pow(x,y,z)的用法
print('x=',pow(2020,1/15))
print('3的3次方除以4的余数:',pow(3,3,4))运行结果如下:

2、利用二分法求解
零点定理即为对于在区间[a,b]上的函数
,若有
,则该函数在区间[a,b]上至少存在一个零点。函数
的单调性与零点原理可知,对于一个区间[0,y]上的数x,必存在一个数
使得
。二分法为任意给定区间[low,high],其中点为两区间的端点值的平均值,记为ans,判断
与y的大小,若
,则令low=ans,high不变;反之
,则令high=ans,low不变;直至
,此时认为ans在误差允许内为y的n次方根(epsilon是给定的误差限)。
以求2020的19次方根为例,代码如下:
y=2020
n=19 #开方次数
epsilon=0.0001 #误差限
num=0 #计算次数
low=0.0 #下限
high=y #上限
ans=(low+high)/2.0 #中点
while abs(ans**n-y)>=epsilon:
num +=1
if ans**n<y:
low=ans
else:
high=ans
ans=(high+low)/2.0
print('num='+str(num)) #二分法计算到误差下限时所需的计算次数(每进行一次二分法操作记一次)
print(str(ans)+' is close to 19root of 2020') 运行结果如下:

3、利用梯度下降法求解
首先定义损失函数(cost function/loss function):
,则可知,当满足
时,L(x)为最小值。因此求解y的n次方根的问题就转化为了求解使函数L(x)最小的x的值。故采用梯度下降法来实现这一目标,梯度下降法的主要迭代式为:
,其中
为学习率(也可表示为Learn_rate),
则为损失函数的导数。
同样以求解2020的19次方根为例,具体代码如下:
def costfunction(x,n,y): #损失函数,即L(x)
return (x**n-y)**2/2
def dcost(x,n,y):
return (x**n-y)*n*x**(n-1) #损失函数的导数,即dL(x)
x=1.5 #初始估计值
y=2020
n=19 #开方数
num=0 #迭代次数
epsilon=0.00001
learn_rate=0.000000001 #学习率
while abs(x**n-y)>=epsilon:
num +=1
x=x-learn_rate*dcost(x,n,y)
print('the 19root of 2020 is x=',x,'迭代次数num=',num)运行结果如下:

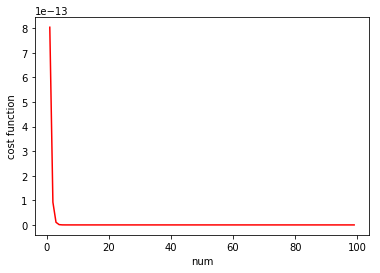
绘制损失函数随迭代次数的变化曲线:
X=[]
Y=[]
for i in range(1,100):
x=x-learn_rate*dcost(x,n,y) #梯度下降法的迭代表达式
X.append(i)
Y.append(costfunction(x,n,y))
plt.plot(X,Y,'r-') #绘制损失函数随迭代次数num的变化图像
plt.xlabel("num")
plt.ylabel("cost function")
plt.show()结果如下:
4、利用牛顿迭代法求解
牛顿迭代法求解一个数的n次方根同梯度下降法类似,都是将问题进行转化;牛顿迭代法是将问题转化为求解函数
的根;主要利用的迭代表达式为
。同样以求解2020的19次方根为例,代码如下:
def f(x,n,y):
return x**n-y #即函数f(x)=x**n-y
def df(x,n,y):
return n*x**(n-1) #函数f(x)的导数
x=2.0 #初始值
y=2020
num=0 #迭代次数
epsilon=0.00001 #误差下限
while abs(x**n-y)>=epsilon:
num +=1
x=x-f(x,n,y)/df(x,n,y)
print('the 19root of 2020 is x=',x,'num=',num)运行结果:

以上就是我总结出的四种求解某个数的n次方根的方法,如果大家还有其他方法也可以留言一起讨论讨论哦!