基于统计和数值分析方法进行动态去除异常值
前言
对于异常值的检验方法很多,针对不同数据集有不同的方法,比如3-sigm原则、聚类方法、箱线图观察法、自编码器观察法等等。本文将介绍一种对于大数据集的有效便捷的异常值检测法,即基于数值分析中拟合技术和统计方法来建立动态规则处理数据中的异常值。

岁月如云,匪我思存,写作不易,望路过的朋友们点赞收藏加关注哈,在此表示感谢!
一:拟合方法原理介绍
-
拟合方法的由来
我们知道,差值曲线必须通过已给的所有数据,这使得我们无法在插值时通过增加节点约束来弱化由于“测不准”而造成的“差异”。那么解决方法就是允许节点上有误差,将“满足节点约束”改为“使在节点的误差总体上最小”,由此产生了在解决实际问题中常用的拟合算。
-
最小二乘拟合方法
最小二乘拟合就是在一类曲线
Φ
\Phi
Φ
中求出一曲线
φ
(
x
)
\varphi(x)
φ
(
x
)
使它与被拟合曲线
f
(
x
)
f(x)
f
(
x
)
在
节点
x
1
,
.
.
.
x
n
x_1,…x_n
x
1
,
.
.
.
x
n
的误差平方和
∑
i
=
1
n
[
f
(
x
i
)
−
φ
(
x
i
)
]
2
\sum_{i=1}^{n}{\left[ f(x_i)-\varphi(x_i) \right]^2}
∑
i
=
1
n
[
f
(
x
i
)
−
φ
(
x
i
)
]
2
最小。
-
举例说明
假如我们从简单的线性拟合出发,即设拟合函数为
φ
(
x
)
=
a
+
b
x
\varphi(x)=a+bx
φ
(
x
)
=
a
+
b
x
,已知
x
1
,
.
.
.
x
n
x_1,…x_n
x
1
,
.
.
.
x
n
及
y
i
=
f
(
x
i
)
(
i
=
1
,
2
,
.
.
.
,
n
)
y_i=f(x_i)(i=1,2,…,n)
y
i
=
f
(
x
i
)
(
i
=
1
,
2
,
.
.
.
,
n
)
,那么由最小二乘法求
f
(
x
)
f(x)
f
(
x
)
的拟合函数由如下步骤:
1:记误差平方和为
e
(
a
,
b
)
=
∑
i
=
1
n
[
y
i
−
φ
(
x
i
)
]
2
=
∑
i
=
1
n
[
y
i
−
(
a
+
b
x
i
)
]
2
e(a,b)=\sum_{i=1}^{n}{\left[ y_i-\varphi(x_i) \right]^2}=\sum_{i=1}^{n}{\left[ y_i-\left( a+bx_i \right) \right]^2}
e
(
a
,
b
)
=
∑
i
=
1
n
[
y
i
−
φ
(
x
i
)
]
2
=
∑
i
=
1
n
[
y
i
−
(
a
+
b
x
i
)
]
2
2:设
∂
e
∂
a
=
∂
e
∂
b
=
0
\frac{\partial e}{\partial a}=\frac{\partial e}{\partial b}=0
∂
a
∂
e
=
∂
b
∂
e
=
0
得
n
a
+
(
∑
i
=
1
n
x
b
)
b
=
∑
i
=
1
n
y
i
na+\left( \sum_{i=1}^{n}{x_b} \right)b=\sum_{i=1}^{n}{y_i}
n
a
+
(
∑
i
=
1
n
x
b
)
b
=
∑
i
=
1
n
y
i
和
(
∑
i
=
1
n
x
i
)
a
+
(
∑
i
=
1
n
x
i
2
)
b
=
∑
i
=
1
n
x
i
y
i
\left( \sum_{i=1}^{n}{x_i} \right)a+\left( \sum_{i=1}^{n}{x_i^2} \right)b=\sum_{i=1}^{n}{x_iy_i}
(
∑
i
=
1
n
x
i
)
a
+
(
∑
i
=
1
n
x
i
2
)
b
=
∑
i
=
1
n
x
i
y
i
当
n
>
1
n>1
n
>
1
时,上式的系数行列式为:
D
=
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
=
n
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
≠
0
D =n\sum_{i=1}^{n}{x_i^2}-\left( \sum_{i=1}^{n}{x_i}\right)^2=n\sum_{i=1}^{n}{\left( x_i-\bar{x} \right)^2}\ne0
D
=
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
=
n
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
=
0
,
其中
x
ˉ
=
1
n
∑
i
=
1
n
x
i
\bar{x}=\frac{1}{n}\sum_{i=1}^{n}{x_i}
x
ˉ
=
n
1
∑
i
=
1
n
x
i
,从而系数
a
,
b
a,b
a
,
b
有唯一解!
-
多项式拟合方法简介
多项式拟合函数是一类基本和常见的拟合函数,常用的理论是对于最小二乘法,再基于由内积运算得来的“法方程组”来确定拟合函数系数,接下来直接给出多项式函数的法方程组。
对于多项式幂函数,
φ
0
(
x
)
=
1
,
φ
1
(
x
)
=
x
,
.
.
,
φ
m
(
x
)
=
x
m
\varphi_0(x)=1,\varphi_1(x)=x,..,\varphi_m(x)=x^m
φ
0
(
x
)
=
1
,
φ
1
(
x
)
=
x
,
.
.
,
φ
m
(
x
)
=
x
m
。由内积运算
(
φ
j
,
φ
k
)
=
∑
i
=
1
n
x
i
j
+
k
,
(
f
,
φ
k
)
=
∑
i
=
1
n
x
i
k
y
i
\left( \varphi_j,\varphi_k \right)=\sum_{i=1}^{n}{x_i^{j+k}},\left( f,\varphi_k \right)=\sum_{i=1}^{n}{x_i^ky_i}
(
φ
j
,
φ
k
)
=
∑
i
=
1
n
x
i
j
+
k
,
(
f
,
φ
k
)
=
∑
i
=
1
n
x
i
k
y
i
,这样得到法方程如下:
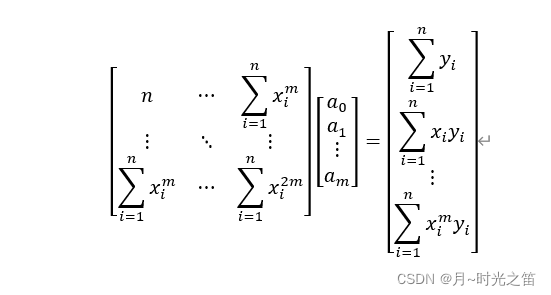
从上述矩阵表达形式我们知道,系数向量
[
a
0
,
a
1
,
.
.
.
a
m
]
\left[ a_0,a_1,…a_m \right]
[
a
0
,
a
1
,
.
.
.
a
m
]
就是求得的最优系数向量。
当
m
m
m
比较大也就是多项式拟合次数过于高时,该线性方程组往往是病态的,幂次运算过大而导致误差过大,所以一般会采用斯密特正交多项式来进行拟合修正,这里将不再过多展开,有兴趣的可以查看相关数值分析资料。
二:建立异常值检测步骤
“拟合”我们在上面也提到过非常适用于大的数据集(插值一般适用于小的数据集),一般情况下,我们会选择3次左右的多项式来进行拟合,达到一种非线性效果,所以当应用于实际数据时我们由如下步骤:
- 对数据进行多项式拟合,选择合理的多项式阶数,
- 对拟合出来的多项式曲线进行上下界的选取,一般会选择拟合出的数据集的标准差倍数,也可以是此数据集的均值倍数等等,
- 把在上下界之外的数据集作为异常值处理。
三:代码实现
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']##中文乱码问题!
plt.rcParams['axes.unicode_minus']=False#横坐标负号显示问题!
choosedata = pd.read_csv('建模数据.csv', index_col=0)
def check_outlier(data,multi):
colls = list(data.columns)##获取数据的所有列名
for i in colls:
plt.figure(figsize=(15,8))
value = data[i]##拟合+统计法
x = [j for j in range(len(value))]
coeffs = np.polyfit(x, value, 3) ##专门求多项式估计参数的函数
p = np.poly1d(coeffs) # 一元估计参数
sigm = p(x).std()
sigm_up = p(x) + multi * sigm
sigm_down = p(x) - multi * sigm
fil_S = value[(value >= sigm_down) & (value <= sigm_up)]#条件筛选
print('\033[1;32m原数据长度:%s,经过异常排除后还剩:%s\033[0m'%(len(value),len(fil_S)))
plt.scatter(x,value,label='原始数值')
plt.plot(p(x),'r',label='拟合曲线')
plt.plot(sigm_up,'g',label='拟合上限曲线')
plt.plot(sigm_down,'b',label='拟合下限曲线')
plt.legend(fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
check_outlier(choosedata,6)
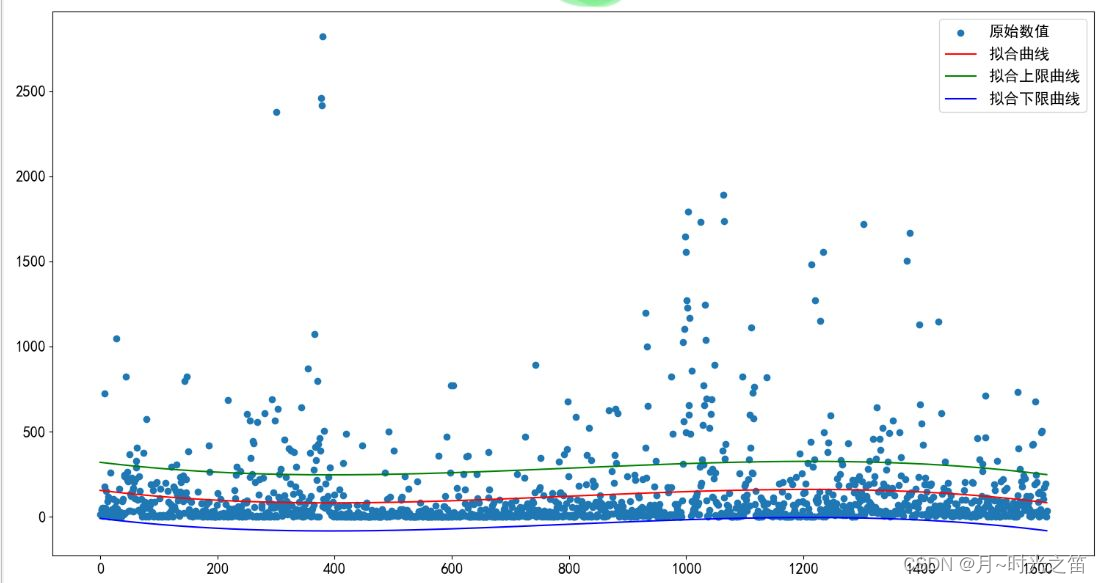
图1
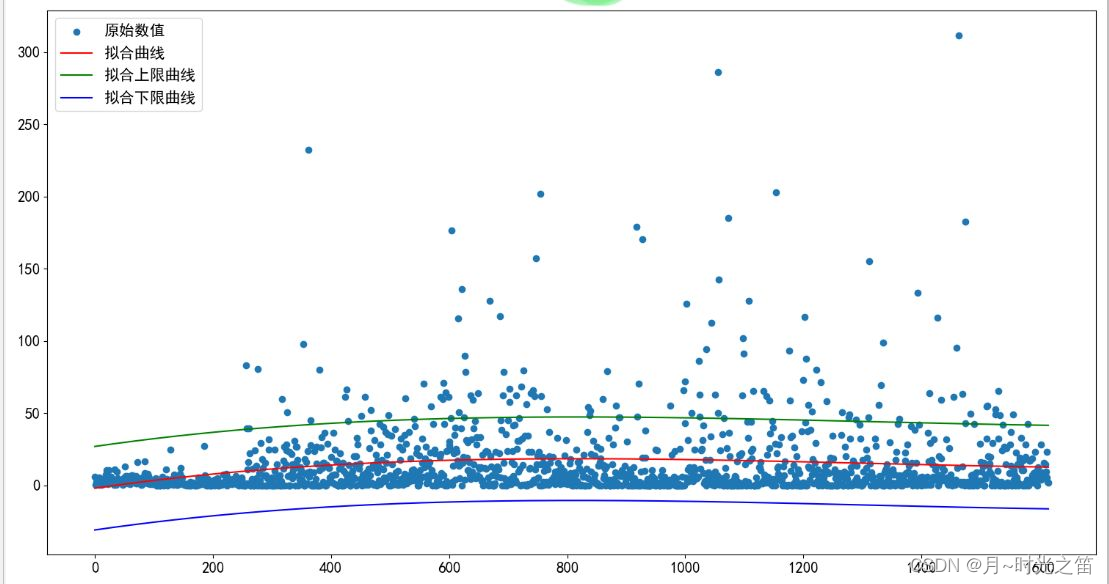
图2

图3
上图中的图1,图2,图3就是我们大致处理异常值的过程。
四:总结
异常值处理方法很多,这种基于统计+数值分析的方法对处理数据量大的情况是比较实用的,能充分展现其高效性。当然,在处理实际问题中,以上逻辑涉及的参数是可以相应变化的,尤其是拟合的上下界范围。