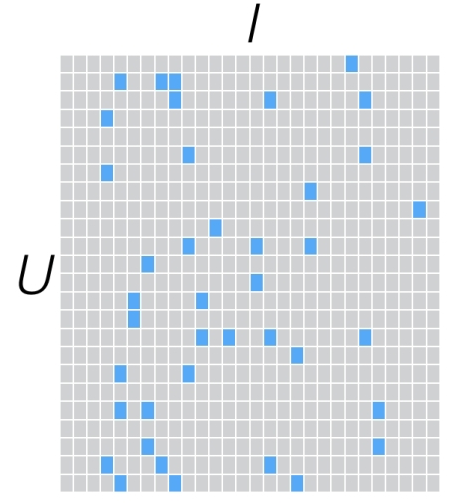
最基本的问题,以用户电影评分为例,也就是这个用户-电影矩阵.
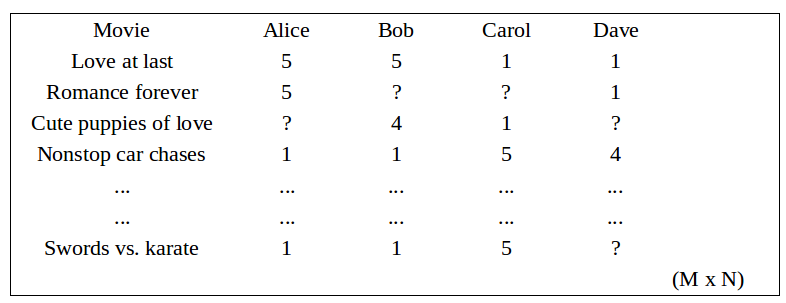
表中是用户多电影的评分,但评分有缺失,因为用户不可能对所有电影作出评价.
那么推荐问题就是给用户合理推荐一个没看过的电影,合理是指,预测用户应该对这部电影评分较高.然后这个问题就变成了矩阵补全,也就是填充表中的问号.
低秩矩阵分解
矩阵的补全有无数种可能,所以如果不对用户-电影矩阵(记为Y)的性质作出一定假设,那这个恢复问题就不可能完成.所以首先作出的假设是Y是低秩的.如果Y是低秩的,那么Y就能够由两个较小的矩阵线性组合而来.即:
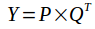
假设Y矩阵维度\(n_m \times n_u\),即有\(n_m\)部电影和\(n_u\)个用户,P的维度是\(n_m \times K\), Q的维度是\(n_u \times K\),K是特征的维度,也就是Y的秩.上式如果画出来就是这样.