【强化学习】Q-Learning详解

https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/2-1-general-rl/ 莫凡大神的有趣的强化学习视频通俗易懂

发现了很多RL资料搬砖过来，刚入门的可以用得上

David Silver 博士的 UCL 公开课：http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html

DeepMind 和 UCL 的DL、RL课程：https://www.youtube.com/playlist?list=PLqYmG7hTraZDNJre23vqCGIVpfZ_K2RZs

Sergey Levine 的DRL课程：http://rail.eecs.berkeley.edu/deeprlcourse/

OpenAI 的 Spinning Up in Deep RL：https://blog.openai.com/spinning-up-in-deep-rl/

关于深度强化学习良心paper：https://arxiv.org/abs/1810.06339

1、算法思想

QLearning是强化学习算法中value-based的算法，Q即为Q（s,a）就是在某一时刻的 s 状态下(s∈S)，采取动作a (a∈A)动作能够获得收益的期望，环境会根据agent的动作反馈相应的回报reward r，所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值，然后根据Q值来选取能够获得最大的收益的动作。

Q-Table	a1	a2
s1	q(s1,a1)	q(s1,a2)
s2	q(s2,a1)	q(s2,a2)
s3	q(s3,a1)	q(s3,a2)

2、公式推导

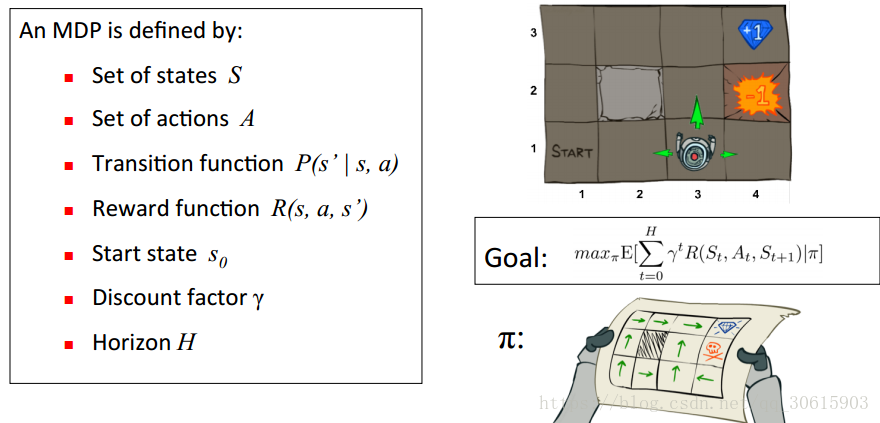
举个例子如图有一个GridWorld的游戏从起点出发到达终点为胜利掉进陷阱为失败。智能体（Agent）、环境状态（environment）、奖励（reward）、动作（action）可以将问题抽象成一个马尔科夫决策过程，我们在每个格子都算是一个状态

s_t

$s_{t}$

, π(a|s)在s状态下采取动作a策略。 P(s’|s,a)也可以写成

′

P_{ss’}^a

$P_{s s^{'}}^{a}$

为在s状态下选择a动作转换到下一个状态s’的概率。R(s’|s,a)表示在s状态下采取a动作转移到s’的奖励reward，我们的目的很明确就是找到一条能够到达终点获得最大奖赏的策略。

这里写图片描述

所以目标就是求出累计奖励最大的策略的期望：

Goal：

⁡

[

∑

(

)

∣

]

\max_πE[\sum_{t=0}^{H}γ^tR(S_t,A_t,S_{t+1}) | π]

$max_{π} E [\sum_{t = 0}^{H} γ^{t} R (S_{t}, A_{t}, S_{t + 1}) ∣ π]$

Qlearning的主要优势就是使用了时间差分法TD（融合了蒙特卡洛和动态规划）能够进行离线学习, 使用bellman方程可以对马尔科夫过程求解最优策略

贝尔曼方程

通过bellman方程求解马尔科夫决策过程的最佳决策序列，状态值函数

(

)

V_\pi(s)

$V_{π} (s)$

可以评价当前状态的好坏，每个状态的值不仅由当前状态决定还要由后面的状态决定，所以状态的累计奖励求期望就可得出当前s的状态值函数V(s)。bellman方程如下

(

)

(

∣

)

V_π(s) = E(U_t|S_t = s)

$V_{π} (s) = E (U_{t} ∣ S_{t} = s)$

(

)

[

]

∣

]

V_π(s) = E_π[R_{t+1}+γ[R_{t+2} + γ[…….]]|S_t = s]

$V_{π} (s) = E_{π} [R_{t + 1} + γ [R_{t + 2} + γ [. . . . . . .]] ∣ S_{t} = s]$

(

)

[

(

′

)

∣

]

V_π(s) = E_π[R_{t+1}+γV(s’)|S_t = s]

$V_{π} (s) = E_{π} [R_{t + 1} + γ V (s^{'}) ∣ S_{t} = s]$

最优累计期望可用

∗

(

)

V^*(s)

$V^{*} (s)$

表示，可知最优值函数就是

∗

(

)

(

)

V^*(s)=max_πV_\pi(s)

$V^{*} (s) = m a x_{π} V_{π} (s)$

∗

(

)

max

⁡

[

∑

(

)

∣

]

V^*(s)=\max_πE[\sum_{t=0}^{H}γ^tR(S_t,A_t,S_{t+1}) | π,s_0=s]

$V^{*} (s) = max_{π} E [\sum_{t = 0}^{H} γ^{t} R (S_{t}, A_{t}, S_{t + 1}) ∣ π, s_{0} = s]$

Q(s,a)状态动作值函数

(

)

[

∣

]

q_π(s,a) = E_π[r_{t+1}+γr_{t+2}+γ^2r_{t+3}+….|A_t=a,S_t=s]

$q_{π} (s, a) = E_{π} [r_{t + 1} + γ r_{t + 2} + γ^{2} r_{t + 3} + . . . . ∣ A_{t} = a, S_{t} = s]$

(

)

[

∣

]

q_π(s,a) = E_π[G_t|A_t=a,S_t=s]

$q_{π} (s, a) = E_{π} [G_{t} ∣ A_{t} = a, S_{t} = s]$

其中

G_t

$G_{t}$

是t时刻开始的总折扣奖励，从这里我们能看出来 γ衰变值对Q函数的影响，γ越接近于1代表它越有远见会着重考虑后续状态的的价值，当γ接近0的时候就会变得近视只考虑当前的利益的影响。所以从0到1，算法就会越来越会考虑后续回报的影响。

(

)

[

(

)

∣

]

q_π(s,a) = E_π[R_{t+1}+γq_π(S_{t+1},A_{t+1})|A_t=a,S_t=s]

$q_{π} (s, a) = E_{π} [R_{t + 1} + γ q_{π} (S_{t + 1}, A_{t + 1}) ∣ A_{t} = a, S_{t} = s]$

最优价值动作函数

∗

(

)

∗

(

)

Q^*(s,a)=max_\pi Q^*(s,a)

$Q^{*} (s, a) = m a x_{π} Q^{*} (s, a)$

,打开期望如下

∗

(

)

∑

′

(

′

∣

)

(

′

)

max

⁡

′

∗

(

′

)

Q^*(s,a)=\sum_{s’} P(s’|s,a)(R(s,a,s’)+γ\max_{a’}Q^*(s’,a’))

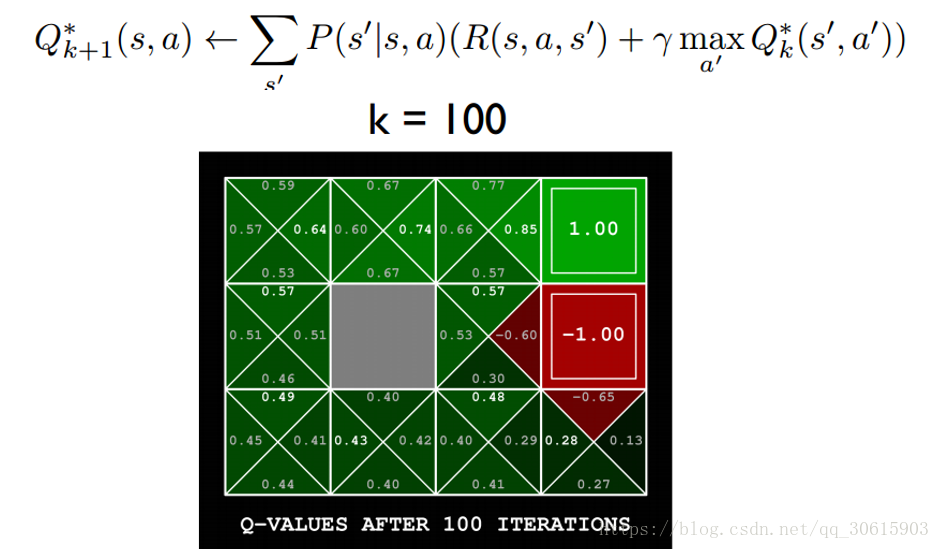
$Q^{*} (s, a) = \sum_{s^{'}} P (s^{'} ∣ s, a) (R (s, a, s^{'}) + γ max_{a^{'}} Q^{*} (s^{'}, a^{'}))$

Bellman方程实际上就是价值动作函数的转换关系

(

)

∑

∈

(

∣

)

(

)

V_π(s) = \sum_{a∈A}π(a|s)q_π(s,a)

$V_{π} (s) = \sum_{a \in A} π (a ∣ s) q_{π} (s, a)$

(

)

∑

′

∈

′

(

′

)

q_π(s,a) = R_s^a + γ\sum_{s’∈S}P_{ss’}^aV_π(s’)

$q_{π} (s, a) = R_{s}^{a} + γ \sum_{s^{'} \in S} P_{s s^{'}}^{a} V_{π} (s^{'})$

(

)

∑

′

∈

(

∣

)

[

∑

′

(

′

)

]

V_π(s)=\sum_{a’∈A}π(a|s)[R_s^a+γ\sum_{s’}P_{ss’}^aV_π(s’)]

$V_{π} (s) = \sum_{a^{'} \in A} π (a ∣ s) [R_{s}^{a} + γ \sum_{s^{'}} P_{s s^{'}}^{a} V_{π} (s^{'})]$

Q值迭代公式

根据下图更直观的了解V(s)与Q(s,a)的关系

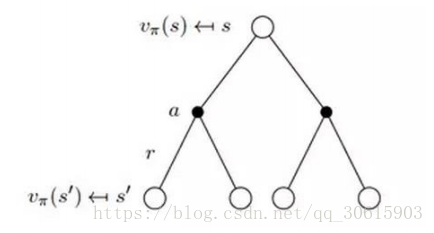
时间差分法 https://blog.csdn.net/qq_30615903/article/details/80821061

时间差分方法结合了蒙特卡罗的采样方法和动态规划方法的bootstrapping(利用后继状态的值函数估计当前值函数)使得他可以适用于model-free的算法并且是单步更新，速度更快。值函数计算方式如下

(

)

←

(

)

(

′

)

−

(

)

V(s)←V(s)+\alpha (R_{t+1}+\gamma V(s’)-V(s))

$V (s) \leftarrow V (s) + α (R_{t + 1} + γ V (s^{'}) - V (s))$

其中

(

′

)

R_{t+1}+\gamma V(s’)

$R_{t + 1} + γ V (s^{'})$

被称为TD目标，

(

′

)

−

(

)

\delta_t=R_{t+1}+\gamma V(s’)-V(s)

$δ_{t} = R_{t + 1} + γ V (s^{'}) - V (s)$

称为TD偏差。

3、更新公式

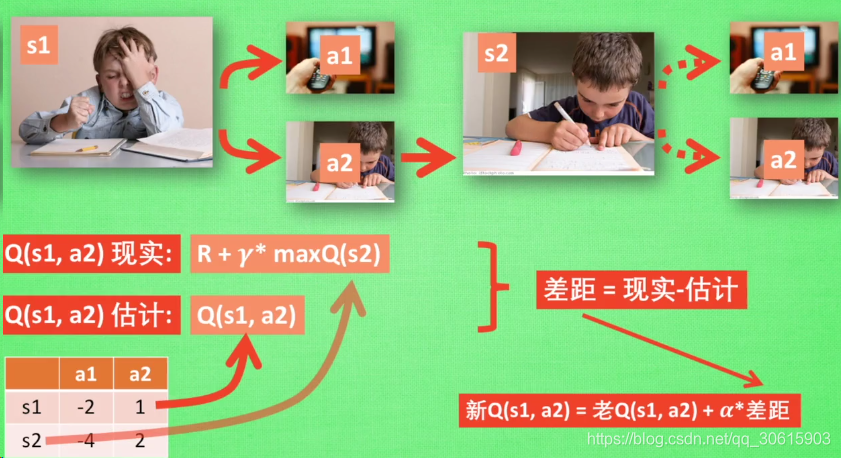
根据以上推导可以对Q值进行计算，所以有了Q值我们就可以进行学习，也就是Q-table的更新过程，其中α为学习率γ为奖励性衰变系数，采用时间差分法的方法进行更新。

(

)

←

(

)

[

′

(

′

)

−

(

)

]

Q(s,a) ← Q(s,a) + α[r + γmax_{a’}Q(s’,a’)-Q(s,a)]

$Q (s, a) \leftarrow Q (s, a) + α [r + γ m a x_{a^{'}} Q (s^{'}, a^{'}) - Q (s, a)]$

上式就是Q-learning更新的公式，根据下一个状态s’中选取最大的

(

′

)

Q(s’,a’)

$Q (s^{'}, a^{'})$

值乘以衰变γ加上真实回报值最为Q现实，而根据过往Q表里面的Q(s,a)作为Q估计。

在这里插入图片描述

这里写图片描述

4、实现代码

代码来自网上各路大神的源码，非原创，据反映没图片跑不通，所以建了个github，https://github.com/xshura/reinforcement_learning

Q-Learning agent

# -*- coding: utf-8 -*-
import random
from environment import Env
from collections import defaultdict


class QLearningAgent:
    def __init__(self, actions):
        # actions = [0, 1, 2, 3]
        self.actions = actions
        self.learning_rate = 0.01
        self.discount_factor = 0.9
        self.epsilon = 0.1
        self.q_table = defaultdict(lambda: [0.0, 0.0, 0.0, 0.0])

    # 采样 <s, a, r, s'>
    def learn(self, state, action, reward, next_state):
        current_q = self.q_table[state][action]
        # 贝尔曼方程更新
        new_q = reward + self.discount_factor * max(self.q_table[next_state])
        self.q_table[state][action] += self.learning_rate * (new_q - current_q)

    # 从Q-table中选取动作
    def get_action(self, state):
        if np.random.rand() < self.epsilon:
            # 贪婪策略随机探索动作
            action = np.random.choice(self.actions)
        else:
            # 从q表中选择
            state_action = self.q_table[state]
            action = self.arg_max(state_action)
        return action

    @staticmethod
    def arg_max(state_action):
        max_index_list = []
        max_value = state_action[0]
        for index, value in enumerate(state_action):
            if value > max_value:
                max_index_list.clear()
                max_value = value
                max_index_list.append(index)
            elif value == max_value:
                max_index_list.append(index)
        return random.choice(max_index_list)


if __name__ == "__main__":
    env = Env()
    agent = QLearningAgent(actions=list(range(env.n_actions)))
    for episode in range(1000):
        state = env.reset()
        while True:
            env.render()
            # agent产生动作
            action = agent.get_action(str(state))
            next_state, reward, done = env.step(action)
            # 更新Q表
            agent.learn(str(state), action, reward, str(next_state))
            state = next_state
            env.print_value_all(agent.q_table)
            # 当到达终点就终止游戏开始新一轮训练
            if done:
                break

环境部分

import time
import numpy as np
import tkinter as tk
from PIL import ImageTk, Image

np.random.seed(1)
PhotoImage = ImageTk.PhotoImage
UNIT = 100
HEIGHT = 5
WIDTH = 5


class Env(tk.Tk):
    def __init__(self):
        super(Env, self).__init__()
        self.action_space = ['u', 'd', 'l', 'r']
        self.n_actions = len(self.action_space)
        self.title('Q Learning')
        self.geometry('{0}x{1}'.format(HEIGHT * UNIT, HEIGHT * UNIT))
        self.shapes = self.load_images()
        self.canvas = self._build_canvas()
        self.texts = []

    def _build_canvas(self):
        canvas = tk.Canvas(self, bg='white',
                           height=HEIGHT * UNIT,
                           width=WIDTH * UNIT)
        # create grids
        for c in range(0, WIDTH * UNIT, UNIT):  # 0~400 by 80
            x0, y0, x1, y1 = c, 0, c, HEIGHT * UNIT
            canvas.create_line(x0, y0, x1, y1)
        for r in range(0, HEIGHT * UNIT, UNIT):  # 0~400 by 80
            x0, y0, x1, y1 = 0, r, HEIGHT * UNIT, r
            canvas.create_line(x0, y0, x1, y1)

        # add img to canvas
        self.rectangle = canvas.create_image(50, 50, image=self.shapes[0])
        self.triangle1 = canvas.create_image(250, 150, image=self.shapes[1])
        self.triangle2 = canvas.create_image(150, 250, image=self.shapes[1])
        self.circle = canvas.create_image(250, 250, image=self.shapes[2])

        # pack all
        canvas.pack()

        return canvas

    def load_images(self):
        rectangle = PhotoImage(
            Image.open("../img/rectangle.png").resize((65, 65)))
        triangle = PhotoImage(
            Image.open("../img/triangle.png").resize((65, 65)))
        circle = PhotoImage(
            Image.open("../img/circle.png").resize((65, 65)))

        return rectangle, triangle, circle

    def text_value(self, row, col, contents, action, font='Helvetica', size=10,
                   style='normal', anchor="nw"):
        if action == 0:
            origin_x, origin_y = 7, 42
        elif action == 1:
            origin_x, origin_y = 85, 42
        elif action == 2:
            origin_x, origin_y = 42, 5
        else:
            origin_x, origin_y = 42, 77

        x, y = origin_y + (UNIT * col), origin_x + (UNIT * row)
        font = (font, str(size), style)
        text = self.canvas.create_text(x, y, fill="black", text=contents,
                                       font=font, anchor=anchor)
        return self.texts.append(text)

    def print_value_all(self, q_table):
        for i in self.texts:
            self.canvas.delete(i)
        self.texts.clear()
        for i in range(HEIGHT):
            for j in range(WIDTH):
                for action in range(0, 4):
                    state = [i, j]
                    if str(state) in q_table.keys():
                        temp = q_table[str(state)][action]
                        self.text_value(j, i, round(temp, 2), action)

    def coords_to_state(self, coords):
        x = int((coords[0] - 50) / 100)
        y = int((coords[1] - 50) / 100)
        return [x, y]

    def state_to_coords(self, state):
        x = int(state[0] * 100 + 50)
        y = int(state[1] * 100 + 50)
        return [x, y]

    def reset(self):
        self.update()
        time.sleep(0.5)
        x, y = self.canvas.coords(self.rectangle)
        self.canvas.move(self.rectangle, UNIT / 2 - x, UNIT / 2 - y)
        self.render()
        # return observation
        return self.coords_to_state(self.canvas.coords(self.rectangle))

    def step(self, action):
        state = self.canvas.coords(self.rectangle)
        base_action = np.array([0, 0])
        self.render()

        if action == 0:  # up
            if state[1] > UNIT:
                base_action[1] -= UNIT
        elif action == 1:  # down
            if state[1] < (HEIGHT - 1) * UNIT:
                base_action[1] += UNIT
        elif action == 2:  # left
            if state[0] > UNIT:
                base_action[0] -= UNIT
        elif action == 3:  # right
            if state[0] < (WIDTH - 1) * UNIT:
                base_action[0] += UNIT

        # 移动
        self.canvas.move(self.rectangle, base_action[0], base_action[1])
        self.canvas.tag_raise(self.rectangle)
        next_state = self.canvas.coords(self.rectangle)
        # 判断得分条件
        if next_state == self.canvas.coords(self.circle):
            reward = 100
            done = True
        elif next_state in [self.canvas.coords(self.triangle1),
                            self.canvas.coords(self.triangle2)]:
            reward = -100
            done = True
        else:
            reward = 0
            done = False

        next_state = self.coords_to_state(next_state)
        return next_state, reward, done

    # 渲染环境
    def render(self):
        time.sleep(0.03)
        self.update()

原文链接：https://blog.csdn.net/qq_30615903/article/details/80739243