引言

当面对大量数据时，我们往往需要从中提取关键信息来进行分析和理解，如何快速、准确地找到数据中的有用模式成为了一项关键任务。例如在

Digit Recognizer

中，每一张手写数字图像都有784个像素点，然而，这784个像素点并不都是我们需要的，因此就需要有一种算法能够帮助我们将其中最主要的特征提取出来。

PCA就是这样一种特征提取的方法，它通过观察数据的分布和变化，找到那些最能够区分不同样本和特征的线性组合。它将原始数据转换到一个新的坐标系中，其中每个坐标轴都对应于数据中的一个主要特征，称为主成分。通过选择保留最重要的主成分，PCA能够将高维数据降低到低维空间，保留了数据中最重要的信息，适用于其它机器学习方法的前处理。主成分的个数通常小于原始变量的个数，因此它也是一种降维方法，关于降维方法的详细介绍，可以参考

这篇博客

。

我们对 PCA 变换的介绍是：先旋转数据，然后删除方差较小的成分。另一种有用的解释是尝试找到一些数字（PCA 旋转后的新特征值），使我们可以将测试点表示为主成分的加权求和。

3.1.3 使用PCA算法进行降维后的效果

四、sklearn中的PCA及其重要参数及接口

4.2.2 inverse_transform

4.2.3 可解释方差比例explained_variance_ratio_

五、PCA的应用

5.1 借助纽约股票市场的周回升率理解PCA

5.2 基于PCA和SVM的MNIST数据集降维与分类

5.3 基于PCA和SVM的特征脸降维及识别

一、主成分分析（PCA）的直观解释

主成分分析（PCA）是一种常用的无监督学习方法，这一方法利用正交变换（也就是对原坐标系做

旋转变换

）把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量称作

主成分

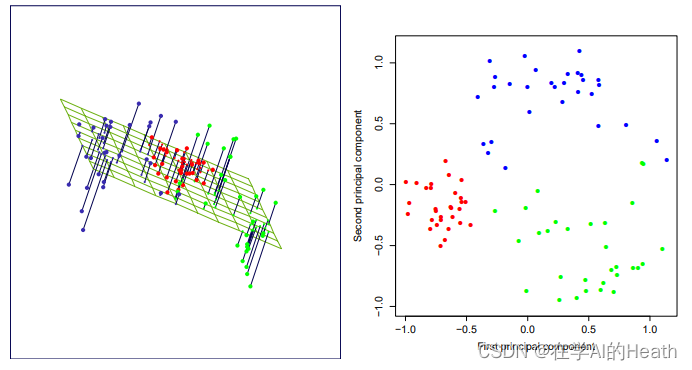
。举一个简单的例子，如下图所示：在三维空间中有一系列的数据点，这些点分布在过原点的平面上。如果我们用自然坐标系x,y,z三个轴来表示数据，就需要使用三个维度。而实际上，这些点可能只出现在一个二维平面上，如果我们通过坐标系旋转变换使得数据所在平面与x,y平面重合，那么我们就可以通过x’,y’两个维度表达原始数据，并且没有任何损失，这样就完成了数据的降维，x’,y’两个轴所包含的信息就是我们要找的主成分。

下面将以数形结合的方法阐述主成分分析的目标：

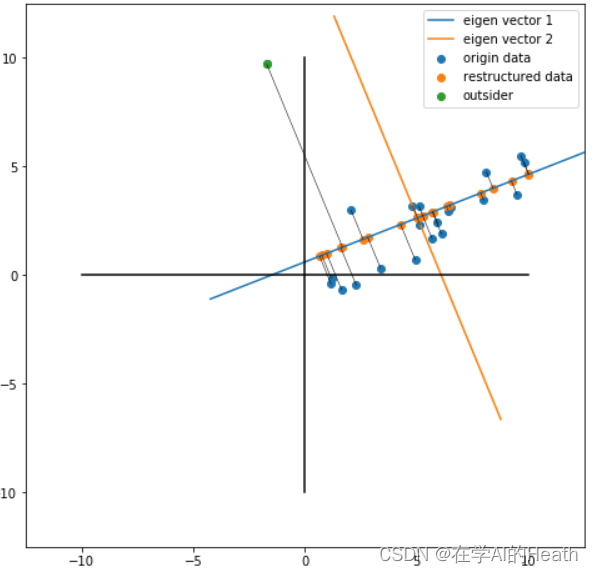
对于上图这组二维样本（蓝色数据点），样本的分布是线性相关的，也就是说，当知道其中一个变量x的取值时，对另一个变量y的预测不是完全随机的。

那么如何使用一条直线(超平面)对所有的样本进行适当的表达？

从图中我们可以看出主成分就是蓝色直线所处的轴，因为在蓝色直线所处的轴上，数据分布（橙色点）更分散，也就意味着数据在这个方向上方差最大。主成分分析选择方差最大的方向（第一主成分）作为新坐标系的第一坐标轴；之后选择与第一坐标轴正交且方差次之的方向（第二主成分）作为新坐标系的第二坐标轴，这里也就意味着选择橙色直线所处的轴为第二坐标轴。经过这样的坐标变换，我们得到了一组全新的坐标系，在这个坐标系中，x和y是

线性无关

的，也就是说，当知道x的取值时，对y的预测是完全随机的。

如何找到这两个坐标轴呢？

将数据去中心化（将坐标原点放在数据中心）
找到坐标系（

找到方差最大的方向

，这个是PCA的

最终目标

）

实际上，像这样的坐标轴，有两个性质：

最大可分性：样本点在这个坐标轴上的投影能尽可能分开。对应PCA最大方差理论。
最近重构性：样本点到这个坐标轴的距离都足够近。对应PCA最小平均误差理论。

在下面的章节中，我将详细解释PCA最大方差理论与PCA最小平均误差理论。

二、对于PCA算法原理的两种解释

算法原理有最大方差理论以及最小平均误差理论，实际上我们将会看到，两种方法是等价的。

2.1 PCA最大方差理论

对于给定的一组数据点
$\left\{ \boldsymbol{v}_1,\boldsymbol{v}_2,\cdots ,\boldsymbol{v}_n \right\}$
，其中所有向量均为列向量，中心化后的表示为
$\left\{ \boldsymbol{x}_1,\boldsymbol{x}_2,\cdots ,\boldsymbol{x}_n \right\} =\left\{ \boldsymbol{v}_1-\boldsymbol{\mu },\boldsymbol{v}_2-\boldsymbol{\mu },\cdots ,\boldsymbol{v}_n-\boldsymbol{\mu } \right\}$
，其中
$\boldsymbol{\mu }=\frac{1}{n}\sum_{i=1}^n{\boldsymbol{v}_i}$
。我们知道，向量内积在几何上表示为第一个向量投影到第二个向量上的长度，因此向量
$\boldsymbol{x}_i$
在
$\boldsymbol{\omega }$
（单位方向向量）上的投影坐标可以表示为（
$\boldsymbol{x}_i$
，
$\boldsymbol{\omega }$
）=
${\boldsymbol{x}_{i}^{T}}\boldsymbol{\omega }$
。所以目标是找到一个投影方向
$\boldsymbol{\omega }$
，使得
$\left\{ \boldsymbol{x}_1,\boldsymbol{x}_2,\cdots ,\boldsymbol{x}_n \right\}$
在
$\boldsymbol{\omega }$
上的投影方差尽可能大。易知，投影之后均值为

0

（因为
$\boldsymbol{\mu }'=\frac{1}{n}\sum_{i=1}^n{\boldsymbol{x}_{i}^{T}}\boldsymbol{\omega }=\left( \frac{1}{n}\sum_{i=1}^n{\boldsymbol{x}_{i}^{T}} \right) \boldsymbol{\omega }$
=

0

,这也是我们进行中心化的意义），因此投影后的方差可以表示为：

$D\left( \boldsymbol{x} \right) =\frac{1}{n}\sum_{i=1}^n{\left( \boldsymbol{x}_{i}^{T}\boldsymbol{\omega } \right) ^2}=\frac{1}{n}\sum_{i=1}^n{\left( \boldsymbol{x}_{i}^{T}\boldsymbol{\omega } \right) ^T}\left( \boldsymbol{x}_{i}^{T}\boldsymbol{\omega } \right) \\ \,\, =\frac{1}{n}\sum_{i=1}^n{\boldsymbol{\omega }^T\boldsymbol{x}_i\boldsymbol{x}_{i}^{T}\boldsymbol{\omega }}=\boldsymbol{\omega }^T\left( \frac{1}{n}\sum_{i=1}^n{\boldsymbol{x}_i\boldsymbol{x}_{i}^{T}} \right) \boldsymbol{\omega }$
（2.1）

仔细一看，
$\frac{1}{n}\sum_{i=1}^n{\boldsymbol{\omega }^T\boldsymbol{x}_i\boldsymbol{x}_{i}^{T}\boldsymbol{\omega }}$
就是样本的协方差矩阵，我们将其写作
$\boldsymbol{\varSigma }$
。另外，由于
$\boldsymbol{\omega }$
是单位方向向量，即有
$\boldsymbol{\omega }^T\boldsymbol{\omega }=1$
。因此我们要求解一个最大化问题，可表示为

$\begin{cases} \max \left\{ \boldsymbol{\omega }^T\boldsymbol{\varSigma \omega } \right\}\\ s.t. \boldsymbol{\omega }^T\boldsymbol{\omega }=1\\ \end{cases}$
（2.2）

引入拉格朗日乘子，并对
$\boldsymbol{\omega }$
求导令其等于

0：

$\boldsymbol{\omega }^T\boldsymbol{\varSigma \omega }-\lambda \left( \boldsymbol{\omega }^T\boldsymbol{\omega }-1 \right)$

$\boldsymbol{\varSigma \omega }-\lambda \boldsymbol{\omega }=0$

便可以推出
$\boldsymbol{\varSigma \omega }=\lambda \boldsymbol{\omega }$
，此时

$D\left( \boldsymbol{x} \right) =\boldsymbol{\omega }^T\boldsymbol{\varSigma \omega }=\lambda \boldsymbol{\omega }^T\boldsymbol{\omega }=\lambda$
（2.3）

原来，
$x$
投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值所对应的特征向量。次佳投影方向位于最佳投影方向的正交空间中，是第二大特征值对应的特征向量，以此类推。

2.2 PCA最小平均误差理论

这和2.2式完全等价。

三、PCA算法的描述及示例

3.1 PCA算法的描述

主成分分析方法主要有两种：第一种方法是通过样本协方差矩阵的特征值分解，求得样本的主成分矩阵；第二种方法是将数据矩阵进行奇异值分解，求得样本的主成分矩阵。

3.1.1 样本协方差矩阵特征值分解法

特征值分解法是根据PCA的基本原理推导而来的算法。PCA的目标是通过线性投影将高维数据映射到低维空间，同时最大化投影后数据的方差。特征值分解提供了一种有效的方式来确定最佳的投影方向，即特征向量。特征值分解法的

具体算法

如下所示:

输入：

样本集
$\boldsymbol{X}=\left\{ \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}},\cdots \boldsymbol{x}_{\boldsymbol{i}},\cdots \boldsymbol{x}_m \right\}$
，其中
$\boldsymbol{X}$
是一个
$n\times m$
的样本矩阵。

低维空间维度数
$d$
。

过程:

1. 对所有样本进行中心化：
$\boldsymbol{x}_{\boldsymbol{i}}\gets \boldsymbol{x}_{\boldsymbol{i}}-\frac{1}{m}\sum_{i=1}^m{\boldsymbol{x}_{\boldsymbol{i}}}$

2. 计算样本的协方差矩阵：
$\boldsymbol{XX}^{\boldsymbol{T}}$

3. 对协方差矩阵
$\boldsymbol{XX}^{\boldsymbol{T}}$
做特征值分解，得到
$m$
个特征值并排序：

$\lambda _1\geqslant \lambda _2\geqslant \cdots \geqslant \lambda _i\geqslant \cdots \geqslant \lambda _m$
；

其中，求前
$d$
个特征值对应的单位特征向量，第
$i$
个特征值对应的单位特征向量：

$\boldsymbol{\omega }_i=\left( a_{1i},a_{2i},\cdots ,a_{mi} \right) ^T,i=1,2,\cdots ,d$

4. 最大的
$d$
个特征值对应的特征向量
$\boldsymbol{\omega }_1,\boldsymbol{\omega }_2,\cdots \boldsymbol{\omega }_d$
，构造矩阵
$\boldsymbol{W}=\left( \boldsymbol{\omega }_1,\boldsymbol{\omega }_2,\cdots \boldsymbol{\omega }_d \right)$
，
$\boldsymbol{W}$
是一个
$n\times d$
的正交矩阵。其中，第
$i$
个样本主成分：

$y_i={\boldsymbol{a}_i}^T\boldsymbol{x}, i=1,2,\cdots ,d$

5. 通过以下映射将
$n$
维样本映射到
$d$
维，得到
$d\times m$
样本主成分矩阵
$\boldsymbol{Y}$
：
$\boldsymbol{Y}=\boldsymbol{W}^T\boldsymbol{X}$

输出：

投影矩阵
$\boldsymbol{W}$
，样本主成分矩阵
$\boldsymbol{Y}$

上述算法可尝试使用numpy一步一步实现。

通过以上算法，我们可以获得一个新的矩阵
$\boldsymbol{Y}$
，新的
$\boldsymbol{Y}$
的第
$d$
维就是
$\boldsymbol{x}_{\boldsymbol{i}}$
在第
$d$
个主成分
$\boldsymbol{\omega }_d$
方向上的投影，通过选取最大的
$d$
个特征值，我们将方差较小的特征（噪声）抛弃，使得每个
$n$
维列向量
$\boldsymbol{x}_{\boldsymbol{i}}$
被映射为
$d$
维列向量
$\boldsymbol{x}_{\boldsymbol{i}}'$
。从第三章的推导中我们可以发现，由于
$\boldsymbol{x}_{\boldsymbol{i}}$
投影后的方差就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值所对应的特征向量。因此降维后前
$d$
个特征值的方差贡献率为
$\eta$
，指定一个阈值
$k$
,则通过求解下列不等式可以求出令方差贡献率达到预定值
$k$
的最小主成分个数
$d$
：

$\eta =\frac{\sum_{i=1}^d{\lambda _i}}{\sum_{i=1}^n{\lambda _i}}\geqslant k$

3.1.2 数据矩阵奇异值分解法

对
$n\times m$
矩阵
$\boldsymbol{X}$
进行奇异值分解：

$\boldsymbol{X}=\boldsymbol{U\varSigma V}^T$

对矩阵
$\boldsymbol{X}$
进行阶段奇异值分解，

保留前
$d$
个奇异值

、奇异向量，
$\boldsymbol{ V}$
的每一列对应一个主成分，得到
$d\times m$
样本主成分矩阵
$\boldsymbol{Y}$
。

$\boldsymbol{Y}=\boldsymbol{V}^{\boldsymbol{T}}\boldsymbol{X}$

在sklearn中，求解PCA的方法正是采用的是奇异值分解法，它大大提高了计算效率，使用

PCA类

时，默认使用svd_solver对数据进行降维。

3.1.3 使用PCA算法进行降维后的效果

PCA将高维空间中的向量通过简单的向量减法和矩阵-向量乘法将新样本投影至低维空间中，降维导致只有
$d$
维被保留，剩余的
$n-d$
个特征值的特征向量都被舍弃了。这个舍弃是有必要的：第一，降维能够使采样密度增大；第二，当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，将它们舍弃能够在一定程度上起到去噪的效果。

在新的特征矩阵生成之前，我们

无法知晓PCA都建立了怎样的新特征向量

，

新特征矩阵生成之后也不具有可读性

。我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而来，新特征虽然带有原始数据的信息，却已经不是原数据上代表着的含义了。因此以PCA为代表的降维算法是

特征提取

的一种表现形式。

四、sklearn中的PCA及其重要参数及接口

4.1 PCA的重要参数

在sklearn中，PCA的表示及默认参数如下所示：

class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, 
svd_solver='auto', tol=0.0, iterated_power='auto', n_oversamples=10, 
power_iteration_normalizer='auto', random_state=None)

官方文档对于参数的解释见

此链接

。下面就比较重要的几种参数进行介绍：

4.1.1 n_compoents

n_components是我们降维后需要的维度，即降维后需要保留的特征数量，降维流程中第二步里需要确认的k值，一般输入[0, min(X.shape)]范围中的整数。如果留下的特征太多，就达不到降维的效果，如果留下的特征太少，那新特征向量可能无法容纳原始数据集中的大部分信息，因此，n_components既不能太大也不能太小。在4.2节，我们绘制累计可解释方差贡献率曲线来确认n_components的值。也可使用最大似然估计自选超参数、按信息量占比选超参数等方法选定此参数值。

4.1.2 svd_solver

参数svd_solver是在降维过程中，用来控制矩阵分解的一些细节的参数。有四种模式可选。关于奇异值分解的原理，请参考

这篇博客

。

表4.1 svd_solver的四种模式
full	从scipy.linalg.svd中调用标准的LAPACK分解器来生成精确完整的SVD，适合数据量比较适中，计算时间充足的情况
arpack	从scipy.sparse.linalg.svds调用ARPACK分解器来运行截断奇异值分解(SVD truncated)，分解时就将特征数量降到n_components中输入的数值k，可以加快运算速度，适合特征矩阵很大的时候，但一般用于特征矩阵为稀疏矩阵的情况，此过程包含一定的随机性
randomized	过Halko等人的随机方法进行随机SVD。Scikit-Learn将使用一种称为Randomized PCA的随机算法，该算法可以快速找到前d个主成分的近似值。它的计算复杂度为O（m×d2）+O（d3），而不是完全SVD方法的O（m×n2）+O（n3）在”full”方法中，分解器会根据原始数据和输入的 n_components值去计算和寻找符合需求的新特征向量，但是在”randomized”方法中，分解器会先生成多个随机向量，然后一一去检测这些随机向量中是否有任何一个符合我们的分解需求，如果符合，就保留这个随机向量，并基于这个随机向量来构建后续的向量空间。这个方法已经被Halko等人证明，比”full”模式下计算快很多，并且还能够保证模型运行效果。适合特征矩阵巨大，计算量庞大的情况。
auto	基于X.shape和n_components的默认策略来选择分解器：如果输入数据的尺寸大于500×500且要提取的特征数小于数据最小维度min(X.shape)的80％，就启用效率更高的”randomized“方法。否则，将使用完全SVD方法”full”，截断将会在矩阵被分解完成后有选择地发生。

4.1.3

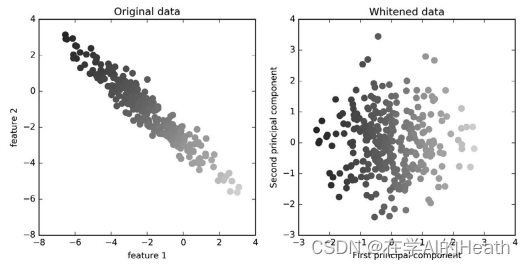
whiten

白化（whitening）选项，它将主成分缩放到相同的尺度。变换后的结果与使用 StandardScaler 相同。再次使用图 3-3 中的数据，白化不仅对应于旋转数据，还对应于缩放数据使其形状是圆形而不是椭圆。

4.2 PCA的重要接口

4.2.1 compoents

compoents就是3.1.1中的矩阵
$\boldsymbol{W}$
，对应的也是下面4.1节中的PCA建立的，让信息尽量聚集的新特征向量。

4.2.2 inverse_transform

inverse_transform可以将归一化，标准化，甚至做过哑变量的特征矩阵还原回原始数据中的特征矩阵，这几乎在向我们暗示，任何有inverse_transform这个接口的过程都是可逆的。

然而，以特征脸数据集为例，PCA降维后，并没有实现数据的完全逆转，这是因为，在降维时，部分信息已经被舍弃了，所以降维后并不会包含原数据100%的信息，所以在逆转的时候，即使维度升高，原数据中已经被舍弃的信息也不可能再回来了。所以，降维不是完全可逆的。这是因为计算主成分矩阵时，特征向量

只保留了前d个向量，但是一定程度上起到了去噪的效果

。

Inverse_transform的功能，是基于X_dr中的数据进行升维，将数据重新映射到原数据所在的特征空间中，而并非恢复所有原有的数据。但同时，我们也可以看出，降维到300以后的数据，的确保留了原数据的大部分信息，所以图像看起来，才会和原数据高度相似，只是稍稍模糊罢了。

具体请参见代码：

人脸识别中conpoents的应用以及inverse

。

4.2.3 可解释方差比例explained_variance_ratio_

这个接口就是3.1.1小节中的方差贡献率
$\eta$
。在4.2节中，我们借助可解释方差比例确定PCA降维后的维度参数n_compoents。

五、PCA的应用

5.1 借助纽约股票市场的周回升率理解PCA

5.2 基于PCA和SVM的MNIST数据集降维与分类

关于MNIST数据集的介绍可以参照

这篇文章

。基于PCA和SVM的MNIST数据集降维与分类这个例子使用的完整代码链接

点击这里

。

首先我们需要做的是确定n_compoents的值（

俗称调参

），首先通过

绘制累计方差贡献率曲线

，找出最佳降维后维度的范围。绘制累计方差贡献率曲线是通过使用sklearn.decomposition.PCA()的属性explained_variance_ratio_实现的。这个属性的范围在0到1之间，可以理解为每个主成分所包含信息量的相对大小。方差比例越大，表示对应主成分所包含的信息量越多，对数据解释能力越强。这个属性可以帮助我们决定保留多少主成分，因此当累积的方差比例达到一定阈值（如95%）时，我们可以认为这些主成分已经解释了绝大部分的数据方差，可以进行降维操作，保留这些主成分。

pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()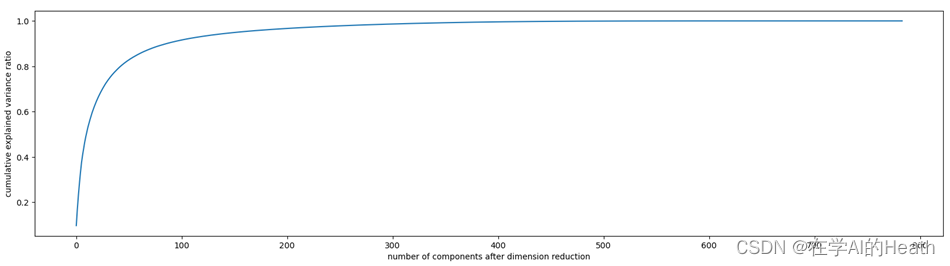

从图4.1中可看出，当维度为100时，累计可解释方差比例达到了90%以上，考虑计算开销等问题，因此维度选取在(0,100)区间内。在0至100范围内

使用随机森林分类器（

RFC）对降维后的数据进行交叉验证的分类性能，绘制不同主成分数量下的分类性能曲线，来帮助选择合适的主成分数量。根据曲线的形状和最高点，可以判断在哪个主成分数量下模型的分类性能最好，以便在实际应用中进行降维操作，结果如图4.2所示。

# time warning
score = []
for i in range(1,101,10):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0)
                           ,X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()

由图4.2可知，交叉验证分类性能在维度为20左右时达到峰值，为进一步确定最佳维度值，在[10,30]范围内再次绘制交叉验证分类性能曲线，结果如图4.3所示。

score = []
for i in range(10,30):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10,30),score)
plt.show()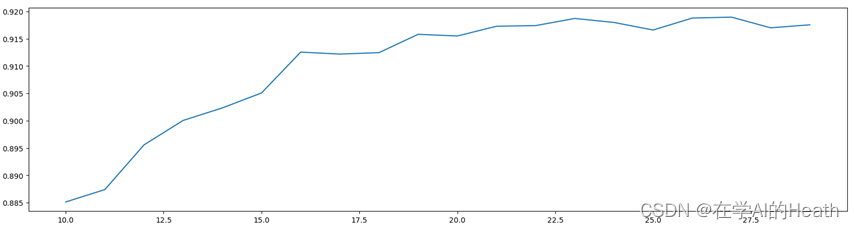

由图4.3可看出，维度的最佳取值约为22，为生成降维后的效果图，考虑时间开销，后续将选取维度为16和22进行数据集降维的测试和验证。选取维度为16时，降维前后的效果对比如图4.4所示。

除了绘制累计可解释方差贡献率曲线之外，n_components的选取也可以使用

最大似然估计法

和

按信息量占比法

。

最大似然估计法：

矩阵分解的理论发展在业界独树一帜，勤奋智慧的数学大神Minka, T.P.在麻省理工学院媒体实验室做研究时找出了让PCA用最大似然估计(maximum likelihood estimation)自选超参数的方法，输入“mle”作为n_components的参数输入，就可以调用这种方法。

pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)
X_mle
#可以发现，mle为我们自动选择了3个特征
pca_mle.explained_variance_ratio_.sum()

按信息量占比法：

输入[0,1]之间的浮点数，并且让参数svd_solver ==’full’，表示希望降维后的总解释性方差占比大于n_components 指定的百分比，即是说，希望保留百分之多少的信息量。比如说，如果我们希望保留97%的信息量，就可以输入 n_components = 0.97，PCA会自动选出能够让保留的信息量超过97%的特征数量。

pca_f = PCA(n_components=0.97,svd_solver="full")
pca_f = pca_f.fit(X)
X_f = pca_f.transform(X)
pca_f.explained_variance_ratio_

进行降维之后使用SVC进行分类，SVC的重要参数经过GridSearchCV确认如下：

clf = SVC(C=bp['C'], kernel='rbf', gamma=bp['gamma'])

最终，选取维度为16和22时，一些相关的参数如下表所示：

表4.1 不同维度下的结果对比(仅供参考)
维度	PCA 运行时间 (s)	可解释方差比例	SVC 运行时间 (s)	训练集准确率	测试集准确率
16	3.139	59.5%	28.2	94.3%	95.7%
22	2.979	66.5%	294.4	95.1%	96.9%

通过比较不同维度的降维结果，我们发现适当降低数据维度仍能保留大部分原始信息，并且能节省计算开销。这对于计算资源有限但又希望进行有效科研的科研人员具有重要意义。同时，降维并不意味着准确率的降低，16维和22维的图像数据在测试集上都能达到95%以上的准确率。

5.3 基于PCA和SVM的特征脸降维及识别

这是sklearn官方文档的示例，

链接点击这里

。基本的思路和方法与4.2所示如出一辙，也是使用PCA降维，将原来的1850维数据降维到150维。并使用precision、recall、F1值和混淆矩阵来对模型效果进行评估。

虽然我们肯定无法理解这些成分的所有内容，但可以猜测一些主成分捕捉到了人脸图像的哪些方面。第一个主成分似乎主要编码的是人脸与背景的对比，第二个主成分编码的是人脸左半部分和右半部分的明暗程度差异，如此等等。虽然这种表示比原始像素值的语义稍强，但它仍与人们感知人脸的方式相去甚远。由于 PCA 模型是基于像素的，因此人脸的相对位置（眼睛、下巴和鼻子的位置）和明暗程度都对两张图像在像素表示中的相似程度有很大影响。但人脸的相对位置和明暗程度可能并不是人们首先感知的内容。在要求人们评价人脸的相似度时，他们更可能会使用年龄、性别、面部表情和发型等属性，而这些属性很难从像素强度中推断出来。重要的是要记住，算法对数据（特别是视觉数据，比如人们非常熟悉的图像）的解释通常与人类的解释方式大不相同。

原文链接：https://blog.csdn.net/ZuHaohua/article/details/131187491

引言

一、主成分分析（PCA）的直观解释

二、对于PCA算法原理的两种解释

2.1 PCA最大方差理论

2.2 PCA最小平均误差理论

三、PCA算法的描述及示例

3.1 PCA算法的描述

3.1.1 样本协方差矩阵特征值分解法

3.1.2 数据矩阵奇异值分解法

3.1.3 使用PCA算法进行降维后的效果

四、sklearn中的PCA及其重要参数及接口

4.1 PCA的重要参数

4.1.1 n_compoents

4.1.2 svd_solver

4.1.3 whiten

4.2 PCA的重要接口

4.2.1 compoents

4.2.2 inverse_transform

4.2.3 可解释方差比例explained_variance_ratio_

五、PCA的应用

5.1 借助纽约股票市场的周回升率理解PCA

5.2 基于PCA和SVM的MNIST数据集降维与分类

5.3 基于PCA和SVM的特征脸降维及识别

你可能也喜欢

4.1.3

whiten