扩频通信系统仿真

文章目录

扩频通信系统仿真
前言
参考资料

前言

主要内容来自参考资料[2]，在学习记录的同时勘正了书中代码的部分错误。

伪随机码

背景知识

扩频通信方系统框图

：

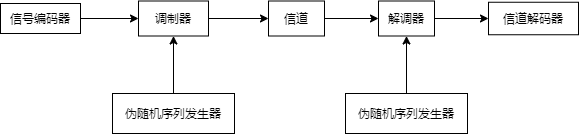
在这里插入图片描述

PN码（Pseudo-Noise Code）

：是一具有与白噪声类似的自相关性质的0和1所构成的编码序列，最广为人知的二位元P-N Code是最大长度位移暂存器序列，简称m-序列，他具有长 2的N次方 – 1个位元，由一具线性回授的m级暂存器来产生。

m序列

：一个r级二进制移位寄存器最多可以取

2^r

$2^{r}$

个不同的状态。对于线性反馈（模二加运算，即异或运算），除全零状态外的

−

2^r-1

$2^{r} - 1$

个状态构成一个周期为

−

N=2^r-1

$N = 2^{r} - 1$

的循环，称该循环输出序列为最大周期线性移位寄存器序列（即m序列）。

不是任意的特征多项式对应的反馈连线都能生成m序列，能够产生m序列的特征多项式

(

)

F(x)

$F (x)$

必须为本原多项式（primitive polynomial）。（距离原理见参考资料

[3]

）

Gold码

：由两个长度相同、速率相同但码字不同的m序列优选对模2加后得到的。

例1

：反馈系统如下图所示，求出其输出的PN序列，并用MATLAB仿真验证。（例子源于参考资料[1]）

在这里插入图片描述

假设初始输入状态为[x1 x2 x3 x4] = [1001]，则由关系式

⊕

x_1=x_3 \oplus x_4\\ x_2=x_1\\ x_3=x_2\\ x_4=x_3

$x_{1} = x_{3} \oplus x_{4} x_{2} = x_{1} x_{3} = x_{2} x_{4} = x_{3}$

容易得出输出序列为

示例代码：

% PN sequence generation
m = 4;%number of flip-flops
N = 2^m-1;%length of PN sequence

%Initial stat of LFSR
x1 = 1;x2 = 0;x3 = 0;x4 = 1;
states = [];
for i = 1:N
    states = [states;x1(i),x2(i),x3(i),x4(i)];
    x1(i+1) = xor(x3(i),x4(i));
    x2(i+1) = x1(i);
    x3(i+1) = x2(i);
    x4(i+1) = x3(i);
end
disp('States of LFSR:');
states

disp('PN sequence:');
pn = x4(1:N)

输出结果为：

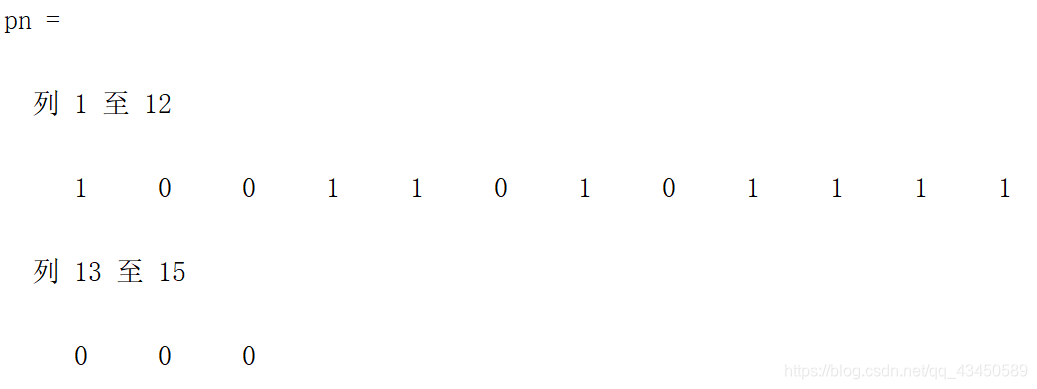
在这里插入图片描述

概率列为m序列，符合平衡性，验证代码如下

noo = sum(pn==1);
noz = sum(pn==0);
if noo == noz+1
    disp('Balance property is satisfied');
end

将0-1序列变换为双极型序列，其中1→-1,0→1。在求其自相关值。示例代码如下：

%Autocorrelation property
for i = 1:N
    if pn(i)==0
        pn1(i)=1;
    else
        pn1(i)=-1;
    end
end

%计算自相关函数
ac = [];
for d = -1:N
    p = circshift(pn1,d);%圆周位移
    ac1 = sum(pn1.*p)/N;
    ac = [ac ac1];
end
d = -1:N;
figure
plot(d,ac,'r-');grid on
xlabel('移位')
ylabel('自相关值')

输出结果如下

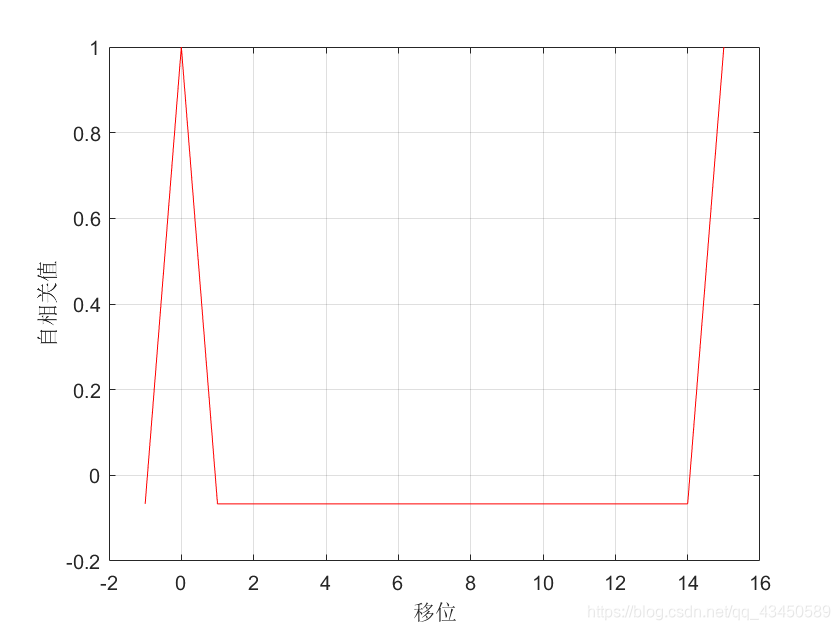
在这里插入图片描述

说明对于m序列，仅在移位值（时延）

⋅

d=m\cdot N,m=0,\pm1,\pm2,…

$d = m \cdot N, m = 0, \pm 1, \pm 2, . . .$

时，自相关值达到最大。可以证明，周期为

N

$N$

的

m

$m$

序列自相关系数理论值为：

{

−

≠

\rho =\left\{\begin{matrix} 1 & j=kN\\ -\frac{1}{N} &j\ne kN \end{matrix}\right.k=0,1,2,…

$ρ = {1 - \frac{1}{N} j = k N j \neq = k N k = 0, 1, 2, . . .$

例2

计算已知正多项式

(

)

F(x)

$F (x)$

的m序列的自相关函数

(

)

F(x) = x^9+x^6+x^4+x^3+1

$F (x) = x^{9} + x^{6} + x^{4} + x^{3} + 1$

示例代码如下

%% 计算已知正多项式的m序列的自相关函数（最高次为9）
clear all;close all
m = 9;N = 2^m-1;
reg = ones(1,9);%寄存器初始状态：全1，寄存器级数为9
coeff = [1 0 0 1 0 1 1 0 0 1];%抽头系数cr,...,c1,c0，取决于特征多项式
for k=1:N
    a1 = mod(sum(reg.*coeff(1:length(coeff)-1)),2);%反馈系数，输入到低位寄存器reg1中
    reg = [reg(2:length(reg)),a1];%移位
    out(k) = reg(1);
end
out = 2*out -1;%转换为双极性序列
%自相关函数
for j = 0:N-1
    rho(j+1) = sum(out.*[out(1+j:N),out(1:j)])/N;
end
j = -N+1:N-1;
rho = [fliplr(rho(2:N)),rho]%镜像翻转
plot(j,rho);
axis([-10 10 -0.1 1.2]);

仿真结果如下：

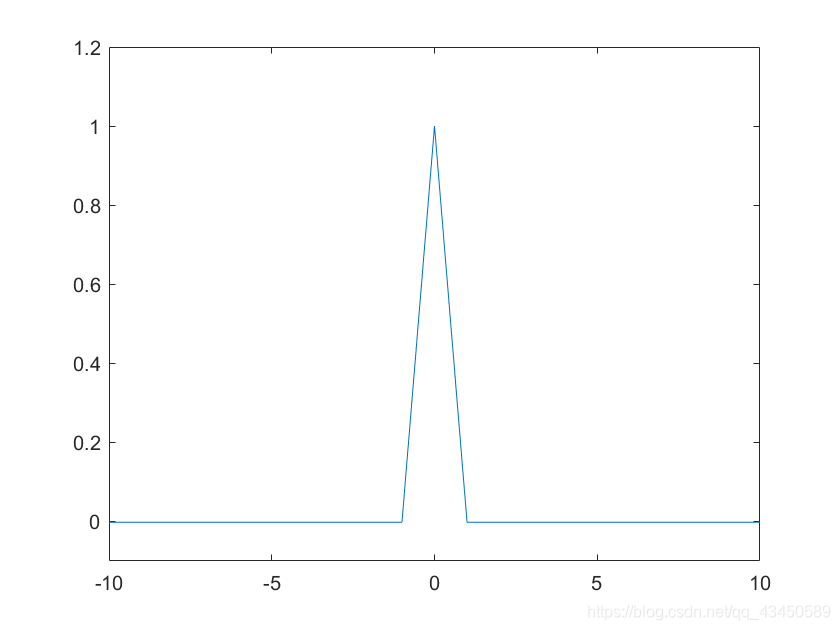
在这里插入图片描述

例3

计算

r=6

$r = 6$

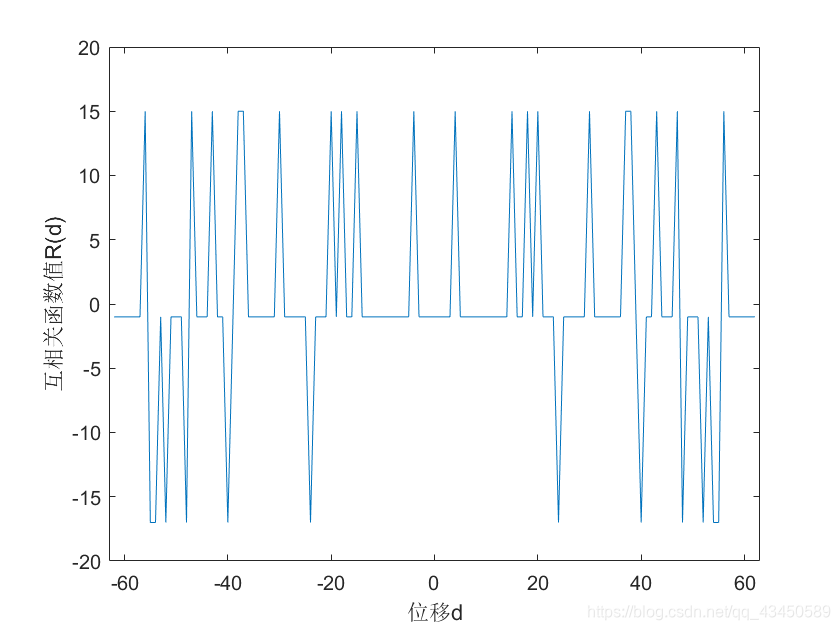
时本原多项式97和115（八进制表示）对应的两个m序列的互相关函数序列

八进制97和115转换二进制分别为1100001和1110011，对应m序列的特征多项式以向量形式表示为[1,1,0,0,0,0,1]和[1,1,1,0,0,1,1]。实现代码如下

clear all;close all
reg = ones(1,6);
coeff = [1 1 0 0 0 0 1];
N = 2^length(reg)-1;
for k = 1:N
    a1 = mod(sum(reg.*coeff(1:length(coeff)-1)),2);
    reg = [reg(2:length(reg)),a1];%序号小的为高位（对应特征多项式的次数高），低位向高位移
    out1(k) = 2*reg(1)-1;%转换为双极性序列
end

reg = ones(1,6);
coeff = [1 1 1 0 0 1 1];
N = 2^length(reg)-1;
for k = 1:N
    a1 = mod(sum(reg.*coeff(1:length(coeff)-1)),2);
    reg = [reg(2:length(reg)),a1];%序号小的为高位（对应特征多项式的次数高），低位向高位移
    out2(k) = 2*reg(1)-1;%转换为双极性序列
end

%两个双极性电平的m序列
for j = 0:N-1
    R(j+1) = sum(out1.*[out2(1+j:N),out2(1:j)]);
end
j = (-N+1):(N-1);
R1 = [fliplr(R(2:N)),R];
plot(j,R1);
xlabel('位移d');ylabel('互相关函数值R(d)');
axis([-N N -20 20]);
max(abs(R))%相关函数绝对值的最大值

运行结果如下：

在这里插入图片描述

直接序列扩频系统

设采用BPSK方式发送二进制信息序列的扩频通信，设信息速率为Rbps，马原间隔为

T_b=1/R_S

$T_{b} = 1 / R_{S}$

，传输信道的有效带宽为

(

)

B_c(B_c>>R)

$B_{c} (B_{c} > > R)$

，调制时，利用PN序列与乘法器，将信息序列带宽扩展为

W=B_c

$W = B_{c}$

。（注：前面说的带宽是信道带宽，而此处为信号带宽）

且引入高斯白噪声与余弦干扰。在接收端产生与发送端相同的PN序列与接收信号相乘，此过程称为解扩，再进行判决，恢复出原始信号。

示例代码如下：

clear all;close all;
Lc = 20;
A1 = 3;%余弦干扰信号幅度
A2 = 7;
A3 = 12;
A4 = 0;
w0 = 1;%以弧度表达的余弦干扰信号频率
SNR_dB = 1:2:30;
%误码率
for i = 1:length(SNR_dB)
    err1(i) = Err_SSC(SNR_dB(i),Lc,A1,w0);
    err2(i) = Err_SSC(SNR_dB(i),Lc,A2,w0);
    err3(i) = Err_SSC(SNR_dB(i),Lc,A3,w0);
end
SNR_dB4 = 0:8;
%无干扰情况下的误码率
for i = 1:length(SNR_dB4)
    err4(i) = Err_SSC(SNR_dB4(i),Lc,A4,w0);
end
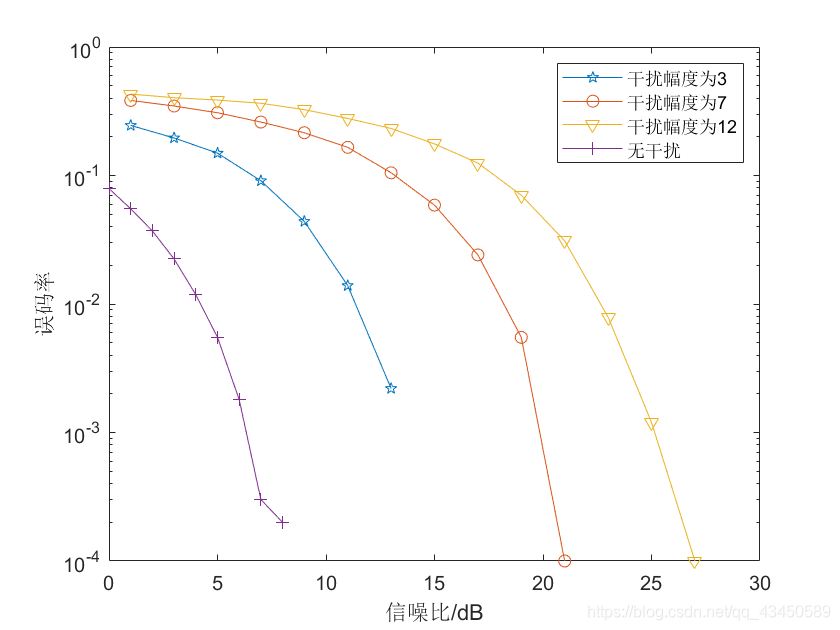
semilogy(SNR_dB,err1,'p-',SNR_dB,err2,'o-',SNR_dB,err3,'v-');
hold on;
semilogy(SNR_dB4,err4,'+-');
legend('干扰幅度为3','干扰幅度为7','干扰幅度为12','无干扰');
xlabel('信噪比/dB');ylabel('误码率');

子函数程序：

function [p] = Err_SSC(SNR_dB,Lc,A,w0)
snr = 10^(SNR_dB/10);%线性表示SNR
sigma = 1;
Eb = 2*sigma^2*snr;%达到设定信噪比所需要的的信号幅度
Ec = Eb/Lc;%每码片能量
N = 10000;%传送比特数目
err_num = 0;
for i = 1:N
    temp = rand;
    if(temp<0.5)
        data = -1;
    else
        data = 1;
    end
    %重复Lc次，为了后续和PN码相乘
    for j = 1:Lc
        repeated_data(j) = data;
    end
    %双极性PN码
    for j = 1:Lc
        temp = rand;
        if(temp<0.5)
            pn(j) = -1;
        else
            pn(j) = 1;
        end
    end
    signal = sqrt(Ec)*repeated_data.*pn;%发送扩频信号
    noise = sigma*randn(1,Lc);%方差为是sigma^2的高斯白噪声
    n = (i-1)*Lc+1:i*Lc;%在总序列的编号，可视为时间序列
    interf = A*cos(w0*n);%干扰interference
    received = signal+noise+interf;%接收信号
    temp = received.*pn;%解码信号,长度为Lc
    decision = sum(temp);
    
    %判决
    if (decision < 0)
        dec = -1;
    else
        dec = 1;
    end
    if(dec ~= data)
        err_num = err_num + 1;
    end
end
p = err_num/N;
end

运行结果如下：

在这里插入图片描述

跳频扩频系统

跳频系统将传输带宽W分为多个互不重叠的频率点，按照信号时间间隔，根据伪随机发生器的输出，选择相应的频率点发送信号。其中，跳频系统的数字调制方式可选择可选择B-FSK或M-FSK。

接收端产生与发射端相同的PN序列，用于控制跳变载波与接收信号的载波同步。在混频器中进行解跳处理。由于在无线信道的情况下，要保持跳频频率合成器的频率同步和信道中产生的信号在跳变时的线性相位是很困难的，故通常选用非相干解调的FSK调制。

下面采用非相干扰解调、平方律判决器（包络判决器），利用MATLAB仿真B-FSK/FH系统在最严重的的部分边带干扰下的性能。

参数说明：

\alpha:

$α :$

干扰占据信道带宽的比值

\rho_b=E_b/J_0,E_b

$ρ_{b} = E_{b} / J_{0}, E_{b}$

为每比特能量，

/J_0

$/ J_{0}$

为干扰的功率谱密度。

示例代码：

%% 跳频扩频系统
clear all;close all;
rou1 = 0:5:35;%仿真抽样误码率
rou2 = 0:0.01:35;
for i=1:length(rou1)
    err_p(i) = BFSK_FH(rou1(i));
end

for i = 1:length(rou2)
    temp = 10^(rou2(i)/10);
    if(temp > 2)
        err_t(i) = 1/(exp(1)*temp);%SNR>2时的理论误码率
    else
        err_t(i) = 0.5*exp(-temp/2);%SNR<2时的理论误码率
    end
end
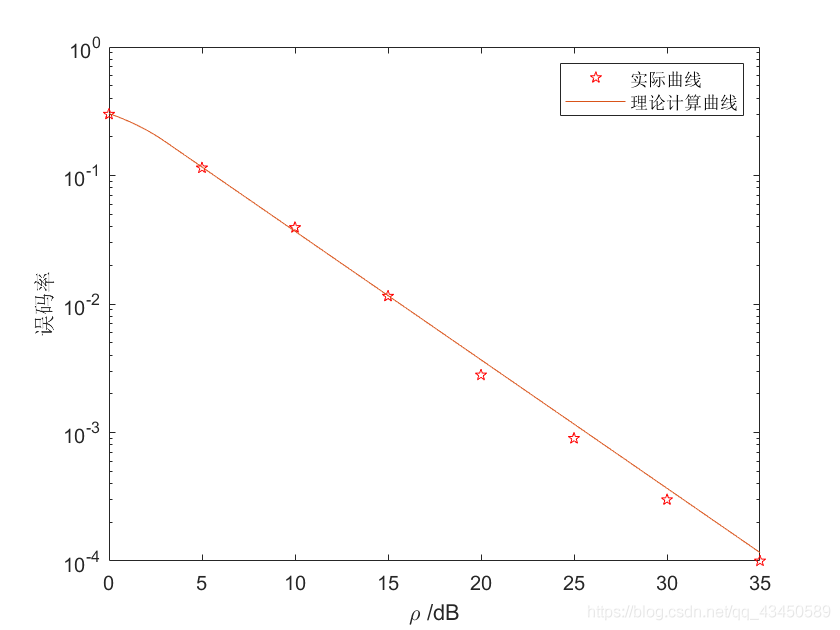
semilogy(rou1,err_p,'rp',rou2,err_t,'-');
legend('实际曲线','理论计算曲线');
xlabel('\rho /dB');ylabel('误码率');

子函数代码：

function [p] = BFSK_FH(rou_dB)
    rou = 10^(rou_dB/10);
    Eb = rou;
    if(rou > 2)
        alpha = 2/rou;
    else
        alpha = 1;
    end
    sigma = sqrt(1/(2*alpha));%噪声标准差
    N = 10000;%传输比特数
    for i = 1:N
        temp = rand;
        if(temp < 0.5)
            data(i) = 1;
        else
            data(i) = 0;
        end
    end

    for i = 1:N
        if(data(i) == 0)    %消息信号正交分量与同相分量的能幅度
            r1c(i) = sqrt(Eb);  r1s(i) = 0;
            r2c(i) = 0;         r2s(i) = 0;
        else
            r1c(i) = 0;         r1s(i) = 0;
            r2c(i) = sqrt(Eb);  r2s(i) = 0;
        end
        
        if(rand < alpha) %以概率α加入噪声并确定接收信号
            r1c(i) = r1c(i) + Gauss(sigma);
            r1s(i) = r1s(i) + Gauss(sigma);
            r2c(i) = r2c(i) + Gauss(sigma);
            r2s(i) = r2s(i) + Gauss(sigma);
        end
    end
    err_num = 0;
    for i = 1:N
        r1 = r1c(i)^2+r1s(i)^2;%第一判决量
        r2 = r2c(i)^2+r2s(i)^2;%第二判决量
        if(r1 > r2)
            dec = 0;
        else
            dec = 1;
        end
        if(dec ~= data(i))
            err_num = err_num+1;
        end
    end
    p = err_num/N;
end

子程序2代码

function [g1,g2] = Gauss(miu,sgma)
%UNTITLED4 此处显示有关此函数的摘要
%   参数判断
if(nargin == 0)
    miu = 0;sgma = 1;
elseif nargin == 1
    sgma = miu;miu = 0;
end
u = rand;%符合均匀分布的随机数
z = sgma*(sqrt(2*log(1/(1-u))));%符合瑞利分布的随机数
u1 = rand;
g1 = miu+z*cos(2*pi*u1);%生成两个统计独立的正态分布的随机数
g2 = miu+z*sin(2*pi*u1);
end

输出结果：

在这里插入图片描述

参考资料

[1]

https://www.youtube.com/watch?v=4pmzJNzdHy4

[2] 《MATLAB通信系统建模与仿真（第2版）》邓奋发编著

[3] m序列产生原理：

https://blog.csdn.net/weixin_45015947/article/details/89891757

原文链接：https://blog.csdn.net/qq_43450589/article/details/113090432