1、根轨迹
前面有讲到通过闭环传递函数的极点分布情况来判断系统是否稳定。当然还有些更简单的判别方式,例如:劳斯稳定性判据、赫尔维茨稳定性判据等。但都是判断系统是否稳定的,那么怎么判断系统的稳定程度(稳定裕度)呢?或者说当一个系统参数在什么范围内系统稳定,取多大时稳定裕度最好。
举个例子:

注意上面的闭环传函为单位负反馈的。那么K的取值是什么范围时该系统稳定呢,当然可以用劳斯判据求出。但K值取多少时最稳定呢,这里就涉及到了根轨迹(系统特征根的轨迹)了。那么我们让K的取值从0到正无穷时,求出闭环传函的特征方程的各个根,这样就形成了根轨迹了。但是这样做要做大量的运算,很复杂耗时。
因此有个工程师发明了一套技巧,不需要每一个具体的K反复求闭环特征根,只需通过开环传递函数Gk(s)的零极点就能得到当开环增益
K
→
∞
K\rightarrow \infty
K
→
∞
时,闭环系统的特征根在复平面上的变化轨迹。
这就是常规根轨迹法。
2、根轨迹定义
根轨迹是开环系统某一参数从零变到无穷时,闭环系统特征方程式的根在s平面上变化的轨迹
3、根轨迹的绘制
只需要利用开环零极点,就能绘制常规根轨迹。
(根据开环零极点,描绘闭环特征根(极点)的曲线)
看下上面的例子用常规根轨迹法,只需要依靠开环零极点:
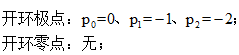
就能得到K从0变化的无穷大时,根的轨迹大概的样子(我们不介绍怎么具体画根轨迹):

下面用matlab绘制上面闭环系统的根轨迹。

从上面可以看出系统的三个极点,本例题中没有零点。而且只有在K 满足一定条件的情况下系统才是稳定的。
在分析系统性能的时候,除了某一根轨迹点对应的开环增益外,有时还需要知道该增益所对应的其他闭环极点的值,这时候则只需输入以下命令即可:[K,p]=rlocfind(sys);然后绘图上出现十字光标,只要点击根轨迹上的一点,命令窗口就会显示出,当前增益K的值,和其他的极点。
程序如下:
>> num=[1]; %开环传函分子多项式系数
den=conv([1,1,0],[1,2]); %开环传函分母多项式系数
sys=tf(num,den); %系统传递函数模型
rlocus(sys) %绘制系统的根轨迹图
[K,p]=rlocfind(sys)
4、根轨迹的作用
1. 从根轨迹的分布直观来说可以看出当K增加至多大时,系统会不稳定。
2. 根轨迹离虚轴越远,那么系统就越不容易因为自身参数K的变化而失去稳定,则系统的稳定程度就越高。
3. 如果系统的稳定程度不足的话,还可以在开环传递函数中增加零点,使得根轨迹左移,增加系统的稳定程度。这样一来,对系统稳定裕度的校正就变的非常直观了。
注意:根轨迹是S域(复频域)设计法,是依靠S来解决问题的。
那么K取值多少时系统比较稳定呢?
借助根轨迹这一工具, 我们可以看出随着系统参数变化,系统极点的分布情况,继而判定系统的稳定性及稳定边界。为获得较好的动稳态性能,常常取阻尼
ξ
\xi
ξ
=0.707
对应的增益为最终的参数值。
首先利用matlab绘制出相应的根轨迹图:
>> s=tf('s');
G=1/s/(s+1)/(s+2);
figure;
rlocus(G)
结果如下图:

从图中可以出:
当K>6.03时,系统存在右半平面极点,系统不再稳定,因此,K应小于6.03。
当K=0.655时,系统阻尼约为0.705,系统的动态性能较佳。
根据上述分析,开环传递函数的最佳增益为0.655。利用step指令,可观察不同K值下,系统的阶跃响应。
s=tf('s');
K=[0.2 0.655 1];
for n=1:3
G=K(n)/s/(s+1)/(s+2);
Gc=feedback(G,1);
step(Gc)
hold on
end

从图中可以看出,K=0.655 确实在响应时间、超调量及调节时间之间得到折中,证实了前述参数设计方法的正确性。