本文可作为
线性代数实现线性回归
的下篇,先简单回顾一下,线性代数实现线性回归中介绍了子空间的概念,把子空间想象成一个超平面,子空间中任意一个向量都可以用子空间的基线性组成,线性回归原理是已知一个超平面和超平面外的一个向量,该向量与在超平面上的投影距离最短,或者说误差最小,在得到这个投影的同时就知道了未知参数,未知参数是投影在子空间基上的坐标。
上篇中介绍的空间是一个由向量组成的空间,向量中元素是实数。 本文将拓展子空间的概念,空间的元素是函数称之为函数空间,这个空间里面有我们熟悉的各种函数以及这些函数的线性组合。函数空间里的子空间是一系列性质相似的函数集合,比如三角函数可以组成一个子空间,由数学分析知道利用三角函数可以实现傅里叶变换,将其他函数表示为三角函数线性组合成的级数形式。本文中选取的空间是一个多项式空间,即其空间里基是x0,x1,x2,x3,…xn…等多项式,需要将其他函数投影到这个子空间里,其运用的知识还是来自于线性代数。
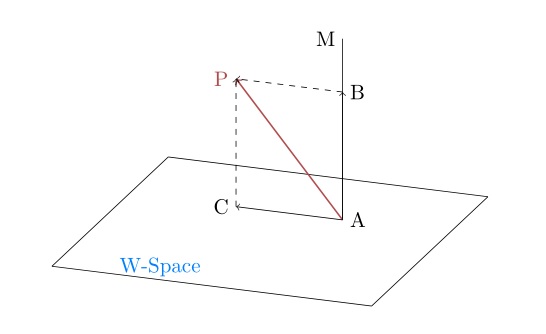
使用上图来说明函数空间,AP代表了函数空间里的一个函数,而下面的平面代表了多项式子空间,AP在多项式空间里的投影AC就是与AP误差最小的多项式,AC是x0,x1,x2,x3,…xn等多项式的线性组合,我们目标就是求出这个线性组合表达式中每个基前面的系数(坐标)。
一、一元多项式逼近任意一元连续函数
这里结合一段python代码说明,这段代码的功能是利用多项式逼近函数f(x)=sin(x)-3cos(x)。
import numpy as np
import math
from sympy import *
from scipy.integrate import tplquad, dblquad, quad
from scipy.linalg import *
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
NSplit_Num = 10000
class polynomialAppro(object):
def __init__(self, split=1000):
self.splitnum = split
pass
def genfunction(self):
ar = []
t = np.linspace(-math.pi, math.pi, self.splitnum)
for x in t:
ar.append(math.sin(x) - 3 * math.cos(x))
sx = np.expand_dims(np.asarray(ar), 0)
return sx
def genpolynomialdata(self):
ar = []
t = np.linspace(-math.pi, math.pi, self.splitnum)
for x in t:
ar.append([1, x, x ** 2, x ** 3, x ** 4, x ** 5])
polynomialdata = np.asarray(ar)
return polynomialdata
if __name__ == '__main__':
appro = polynomialAppro(NSplit_Num)
sx = appro.genfunction() # 1.1
b = sx.T # 1.2
A = appro.genpolynomialdata() # 1.3
ATAminus = np.linalg.inv(np.dot(A.T, A)) # 1.4
coordinate = np.round(np.dot(ATAminus, np.dot(A.T, b)), 4) # 1.5
# 打印图像验证
x = np.linspace(-math.pi, math.pi, NSplit_Num)
y_x = coordinate[0]+ coordinate[1] * x + coordinate[2] * (x ** 2)+ coordinate[3] * (x ** 3) + coordinate[4] * (
x ** 4) + coordinate[5] * (x ** 5)
plt.figure()
plt.subplot(121)
plt.title('原函数图像')
plt.plot(x, b[..., 0])
plt.subplot(122)
plt.title('多项式逼近的函数图像')
plt.plot(x, y_x)
plt.show()
来看下模拟的效果图:
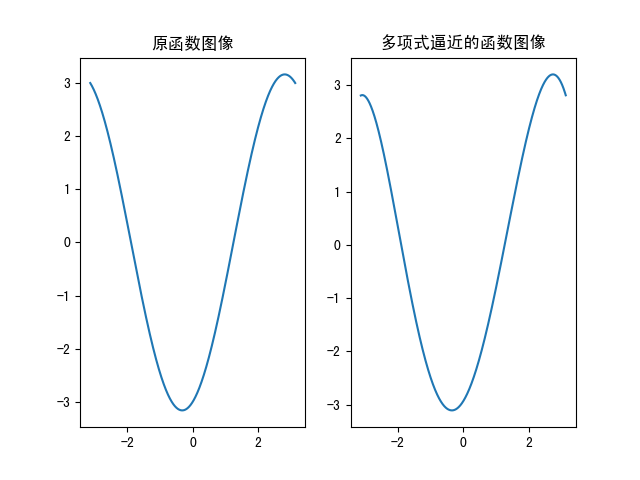
可以看到利用线性回归求出的多项式函数可以较好的逼近目标函数,下面就代码中标红色部分说明:
#1.1 sx=appro.genfunction()
这里是得到目标函数f(x)=sin(x)-3cos(x)在-π ,π之间的数据,将其离散化变成计算机可以处理的向量形式,这里是为了说明采用了显式函数结构,真实的应用中可以是采集而来样本数据。
#1.2 b=sx.T
为了后期处理方便,将其处理成10000*1的向量形式。
#1.3 A=appro.genpolynomialdata()
选取x0,x1,x2,x3,x4,x5作为子空间的基,并将其向量化,这里将得到一个10000*6的矩阵,此时A就是在介绍线性回归问题时的子空间。这里将函数空间元素赋值,使一个函数空间问题变为一个线性代数问题,这种离散化数据手段在计算机处理中会经常使用。
#1.4、1.5
ATAminus=np.linalg.inv( np.dot(A.T,A))
coordinate= np.round(np.dot(ATAminus,np.dot(A.T,b)),4)
经过前面离散化处理,此时问题就变成利用线性空间求解线性回归问题,#1.4、1.5 是求出函数f(x)=sin(x)-3cos(x)在多项式子空间上的投影,这个处理过程 在之前已经讨论过,这里再复盘一遍。
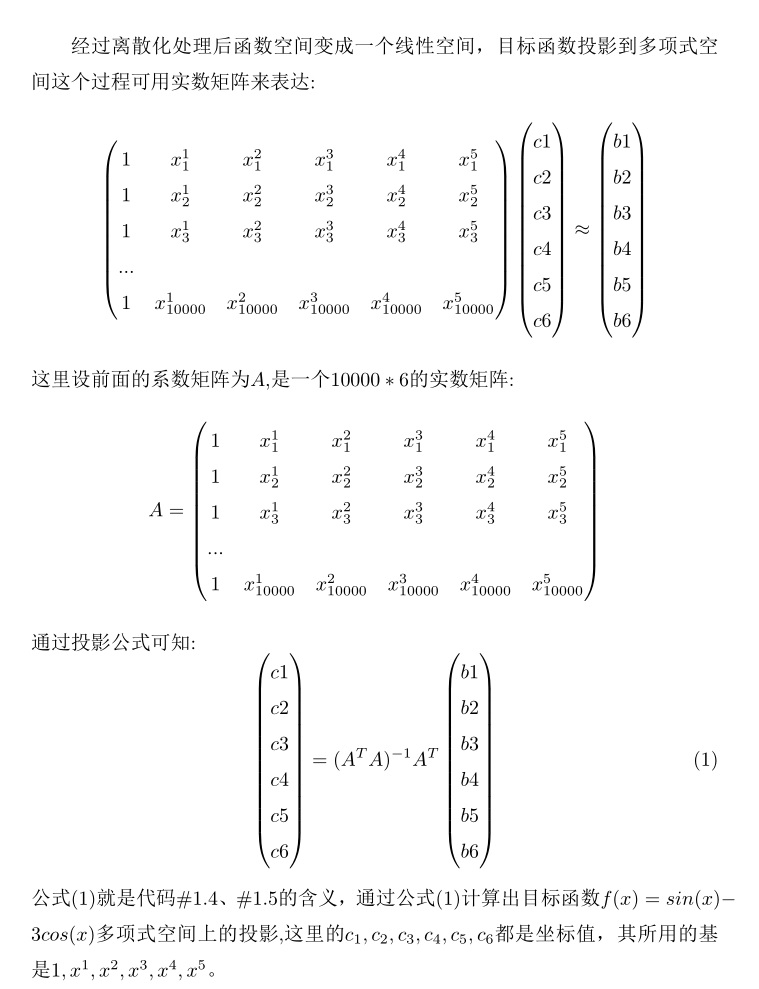
二、 二元多项式逼近任意连续二元连续函数
二元乃至多元多项式逼近任意连续函数与一元函数类似,都是最终转化为实数矩阵形式,然后利用公式(1)求解系数,只不过在构造多项式形式上略有不同,掌握二元多项式逼近问题即可推广至任意元函数的情形,这里还是先展示一段python代码。
from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D import numpy as np import math fig = plt.figure() #定义新的三维坐标轴 ax3 = fig.add_subplot(211,projection='3d') ax2 = fig.add_subplot(212,projection='3d') #定义三维数据 NSTP=500 nstart=-math.pi nend= math.pi Lens= nend-nstart xx = np.arange(nstart,nend,Lens/NSTP) yy = np.arange(nstart,nend,Lens/NSTP) X, Y = np.meshgrid(xx, yy) Z = np.sin(X)-np.cos(Y) ar=[] tempa=[] for x in xx: for y in yy: ar.append( math.sin(x)-math.cos(y)) tempa.append([1,(y**1) ,(y**2) ,(y**3) , (x**1) ,(y**1)*(x**1),(y**2)*(x**1) ,(x**1)*(y**3),(x**2)*(y**0),(x**2)*(y**1),(x**2)*(y**2),(x**2)*(y**3) ,(x**3)*(y**0),(x**3)*(y**1),(x**3)*(y**2),(x**3)*(y**3)])#2.1 pass A=np.array(tempa) b=np.array(ar).reshape([NSTP**2,1]) aminus = np.linalg.inv(np.dot(A.T, A)) temp = np.dot(A.T, b) c = np.dot(aminus, temp) #作图验证 Z2 = c[0,0]*1+ c[1,0]*Y + c[2,0]*(Y**2) + c[3,0]*(Y**3) + c[4,0]*(X**1) + c[5,0]*(X**1)*(Y**1) + c[6,0]*(X**1)*(Y**2) + c[7,0]*(X**1)*(Y**3) + c[8,0]*(X**2) + c[9,0]*(X**2)*(Y**1)+ c[10,0]*(X**2)*(Y**2) + c[11,0]*(X**2)*(Y**3) + c[12,0]*(X**3) + c[13,0]*(X**3)*(Y**1) + c[14,0]*(X**3)*(Y**2)+ c[15,0]*(X**3)*(Y**3) ax3.plot_surface(X,Y,Z,cmap='Blues') ax2.plot_surface(X,Y,Z2,cmap='Greens') #ax3.contour(X,Y,Z, zdim='z',offset=-2,cmap='rainbow) #等高线图,要设置offset,为Z的最小值 plt.show()
效果图如下,上面是目标函数f(x,y)=sin(x)-cos(y)图像,下面是多项式拟合的函数图像:
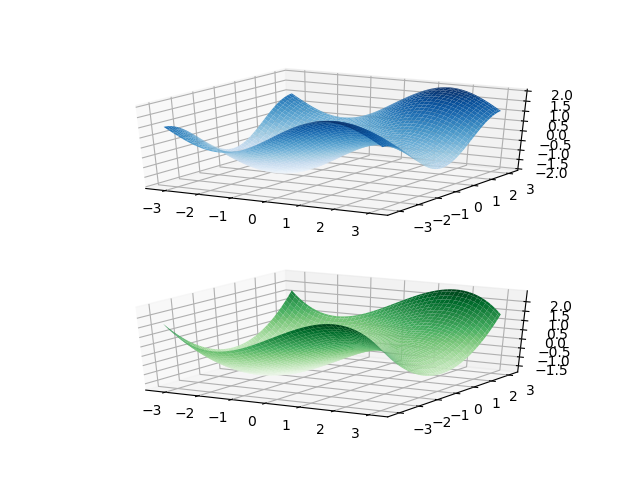
可以发现多元函数求解系数与一元函数一模一样,可以完全使用一元函数时所使用的代码,如上面的红色区域,唯一不同的是这里是二元函数,本例选择多项式最高为6次,即X,Y最高次数为3次,可以选择更高次数以加强精确度。这里需要关心的问题是次数定下来后,基的组合有哪些,既然说到组合,首先想到应该是组合数学。
余下文章链接
多项式逼近