一、回归方法以说明
回归主要有两种类型:
-
多元回归:
y=
β
0
+
β
1
x
1
+
.
.
.
+
β
p
x
p
y = {\beta _0} + {\beta _1}{x_1} + … + {\beta _p}{x_p}
y
=
β
0
+
β
1
x
1
+
…
+
β
p
x
p
-
多项式回归:
y=
β
0
+
β
1
x
1
+
.
.
.
+
β
p
x
p
y = {\beta _0} + {\beta _1}{x^{1}} + … + {\beta _p}{x^{p}}
y
=
β
0
+
β
1
x
1
+
…
+
β
p
x
p
区别就是:
X
∈
[
x
1
,
x
2
,
.
.
.
,
x
n
]
X \in [{x_1},{x_2},…,{x_n}]
X
∈
[
x
1
,
x
2
,
…
,
x
n
]
或者是
X
∈
[
x
1
,
x
2
,
.
.
.
,
x
n
]
X \in [{x^1},{x^2},…,{x^n}]
X
∈
[
x
1
,
x
2
,
…
,
x
n
]
Matlab指令说明
多元回归:
1、确定回归系数的点估计值,命令为:b=regress(Y, X )
1)b表示:
b
=
[
β
^
0
β
^
1
.
.
.
β
^
p
]
b=\left[ \begin{matrix} {
{
{\hat{\beta }}}_{0}} \\ {
{
{\hat{\beta }}}_{1}} \\ … \\ {
{
{\hat{\beta }}}_{p}} \\ \end{matrix} \right]
b
=
⎣
⎡
β
^
0
β
^
1
…
β
^
p
⎦
⎤
2)Y表示:
Y
=
[
Y
1
Y
2
.
.
.
Y
n
]
Y=\left[ \begin{matrix} {
{Y}_{1}} \\ {
{Y}_{2}} \\ … \\ {
{Y}_{n}} \\ \end{matrix} \right]
Y
=
⎣
⎡
Y
1
Y
2
…
Y
n
⎦
⎤
3)X表示:
X
=
[
1
x
11
x
12
.
.
.
x
1
p
1
x
21
x
22
.
.
.
x
2
p
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
x
n
1
x
n
2
.
.
.
x
n
p
]
X=\left[ \begin{matrix} 1 & {
{x}_{11}} & {
{x}_{12}} & … & {
{x}_{1p}} \\ 1 & {
{x}_{21}} & {
{x}_{22}} & … & {
{x}_{2p}} \\ … & … & … & … & … \\ 1 & {
{x}_{n1}} & {
{x}_{n2}} & … & {
{x}_{np}} \\ \end{matrix} \right]
X
=
⎣
⎡
1
1
…
1
x
11
x
21
…
x
n
1
x
12
x
22
…
x
n
2
…
…
…
…
x
1
p
x
2
p
…
x
n
p
⎦
⎤
2、求回归系数的点估计和区间估计、并检验回归模型,命令为:[b, bint,r,rint,stats]=regress(Y,X,alpha)
1) bint表示回归系数的区间估计.
2) r表示残差.
3) rint表示置信区间.
4) stats表示用于检验回归模型的统计量,有三个数值:相关系数
r
2
{
{r}^{2}}
r
2
、F值、与F对应的概率p.
-
说明:相关系数
r2
{
{r}^{2}}
r
2
越接近1,说明回归方程越显著;
F>
F
1
−
α
(
k
,
n
−
k
−
1
)
F>{
{F}_{1-\alpha }}(k,n-k-1)
F
>
F
1
−
α
(
k
,
n
−
k
−
1
)
时拒绝
H0
{
{H}_{0}}
H
0
,F越大,说明回归方程越显著;与F对应的概率
p<
α
p<\alpha
p
<
α
时拒绝
H0
{
{H}_{0}}
H
0
,回归模型成立.
5)alpha表示显著性水平(缺省时为0.05)
3、画出残差及其置信区间,命令为:rcoplot(r,rint)
多项式回归:
1、确定回归系数的点估计值,命令为:A = polyfit(X,y,degress)
1)b表示:
b
=
[
β
^
0
β
^
1
.
.
.
β
^
p
]
b=\left[ \begin{matrix} {
{
{\hat{\beta }}}_{0}} \\ {
{
{\hat{\beta }}}_{1}} \\ … \\ {
{
{\hat{\beta }}}_{p}} \\ \end{matrix} \right]
b
=
⎣
⎡
β
^
0
β
^
1
…
β
^
p
⎦
⎤
2)Y表示:
Y
=
[
y
1
y
2
.
.
.
y
n
]
Y=\left[ \begin{matrix} {
{y}_{1}} \\ {
{y}_{2}} \\ … \\ {
{y}_{n}} \\ \end{matrix} \right]
Y
=
⎣
⎡
y
1
y
2
…
y
n
⎦
⎤
3)X表示:
X
=
[
x
1
x
2
.
.
.
x
n
]
X=\left[ \begin{matrix} {
{x}_{1}} \\ {
{x}_{2}} \\ … \\ {
{x}_{n}} \\ \end{matrix} \right]
X
=
⎣
⎡
x
1
x
2
…
x
n
⎦
⎤
二、题目
2.1 多元回归
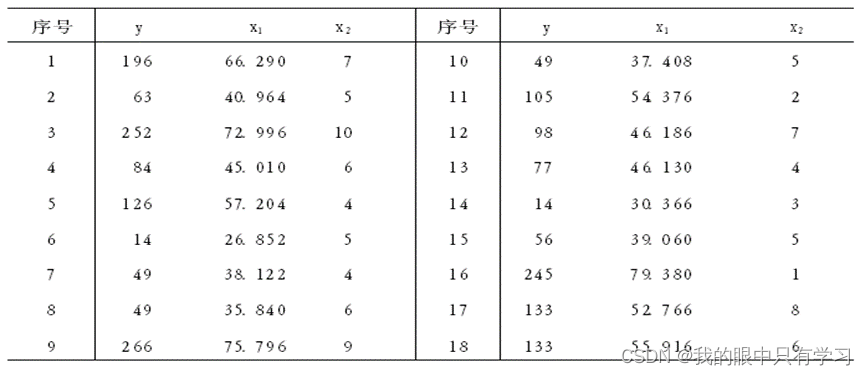
下表列出了某城市18 位35 岁~44 岁经理的年平均收入x1 千元,风险偏好度x2 和人寿保险额y 千元的数据,其中风险偏好度是根据发给每个经理的问卷调查表综合评估得到的,它的数值越大,就越偏爱高风险.研究人员想研究此年龄段中的经理所投保的人寿保险额与年均收入及风险偏好度之间的关系。
研究者预计,经理的年均收入和人寿保险额之间存在着二次关系,并有把握地认为风险偏好度对人寿保险额有线性效应,但对风险偏好度对人寿保险额是否有二次效应以及两个自变量是否对人寿保险额有交互效应,心中没底。
请你通过表中的数据来建立一个合适的回归模型,验证上面的看法,并给出进一步的分析.
2.2 多项式回归
某种合金的主要成分是金属甲与金属乙。经试验与分析,发现这两种金属成分所占的百分比之和
x
x
x
与金属的膨胀系数
y
y
y
之间有一定的相关关系。先测试了13次,得数据如下:
|
x i x_{i} x i |
37.0 | 37.5 | 38.0 | 38.5 | 39.0 | 39.5 | 40.0 | 40.5 | 41.0 | 41.5 | 42.0 | 42.5 | 43.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
y i y_{i} y i |
3.40 | 3.00 | 3.00 | 2.27 | 2.10 | 1.83 | 1.53 | 1.70 | 1.80 | 1.90 | 2.35 | 2.54 | 2.90 |
试建立
x
x
x
与
y
y
y
之间的经验公式。
三、求解以代码实现
3.1 多元回归
由数据结构可以推测该回归可以为,二元回归
y
=
a
1
x
1
+
a
2
x
2
y={
{a}_{1}}{
{x}_{1}}+{
{a}_{2}}{
{x}_{2}}
y
=
a
1
x
1
+
a
2
x
2
编程求解
y
=
a
1
x
1
+
a
2
x
2
y={
{a}_{1}}{
{x}_{1}}+{
{a}_{2}}{
{x}_{2}}
y
=
a
1
x
1
+
a
2
x
2
:
y = [196,63,252,84,126,14,49,49,266,49,105,98,77,14,56,245,133,133]';
x1 = [66.290,40.964,72.996,45.010,57.204,26.852,38.122,35.840,75.796,...
37.408,54.376,46.186,46.130,30.366,39.060,79.380,52.766,55.916]';
x2 = [7,5,10,6,4,5,4,6,9,5,2,7,4,3,5,1,8,6]';
X = [ones(size(x1)) x1 x2];
A = regress(y,X);
结果截图:

于是可得:
f
(
x
)
=
−
158.7676
+
4.8434
∗
x
1
+
5.2014
∗
x
2
f(x)=-158.7676+4.8434*{
{x}_{1}}+5.2014*{
{x}_{2}}
f
(
x
)
=
−
158.7676
+
4.8434
∗
x
1
+
5.2014
∗
x
2
3.2 多项式回归
由数据结构可以推测该回归可以为,多项式回归
y
=
∑
i
=
1
a
i
x
i
y=\sum\limits_{i=1}{
{
{a}_{i}}{
{x}^{i}}}
y
=
i
=
1
∑
a
i
x
i
编程求解
y
=
∑
i
=
1
a
i
x
i
y=\sum\limits_{i=1}{
{
{a}_{i}}{
{x}^{i}}}
y
=
i
=
1
∑
a
i
x
i
在不同阶数的多项式中,RMSE得分的变化:
x = [37.0 37.5 38.0 38.5 39.0 39.5 40.0 40.5 41.0 41.5 42.0 42.5 43.0];
y = [3.40 3.00 3.00 2.27 2.10 1.83 1.53 1.70 1.80 1.90 2.35 2.54 2.90];
for degress = 1:10
A = polyfit(x,y,degress);
y_pred = polyval(A,x);
RMSE(degress,1) = sqrt(mean((y_pred - y).^2));
end
figure;
plot(1:1:10,RMSE,'r-');
legend('RMSE得分变化');
结果截图:
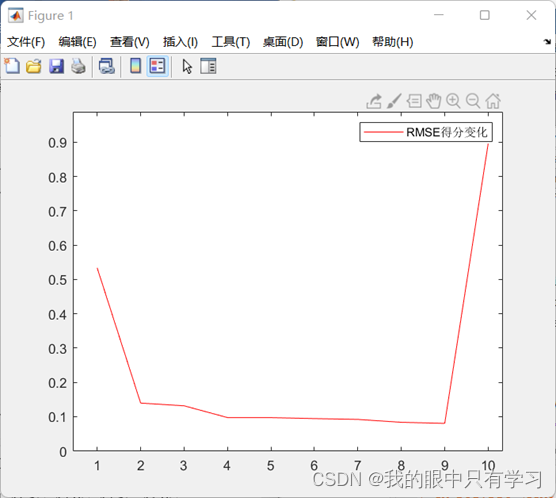
由图可以看出,在i=2的时候,多项式的拟合效果已经很好了,后续增加系数对模型的拟合效果增幅没有很大影响,为了使模型更加方便计算,我们选择使用二次多项式作为经验公式:
A = polyfit(x,y,2)
结果截图:

最终可得经验公式为:
f
(
x
)
=
0.1660
−
13.3866
∗
x
+
271.6231
∗
x
2
f(x)=0.1660-13.3866*x+271.6231*{
{x}^{2}}
f
(
x
)
=
0.1660
−
13.3866
∗
x
+
271.6231
∗
x
2