一般说“感知机”指的是“朴素感知机”,即使用阶跃函数为激活函数的单层感知机;
而“多层感知机”就是指神经网络,即使用sigmoid函数等平滑的激活函数的多层网络。
激活函数activation function:把输入信号的总和转换为输出信号的转换器。
它的关键在于如何去激活输入信号的总和。
(1)阶跃函数
h
(
x
)
=
{
1
,
x
>
0
0
,
x
≤
0
h(x)=\left\{ \begin{aligned} 1,x>0\\ 0,x\leq0 \end{aligned} \right.
h
(
x
)
=
{
1
,
x
>
0
0
,
x
≤
0
def step_function(x): # 参数x只能接收实数
if x>0:
return 1
else:
return 0
import numpy as np
import matplotlib.pylab as plt
def step_func(x): # 参数x可以接受numpy数组
y = x > 0 # y是布尔型数组
return y.astype(np.int)
x = np.arange(-5., 5., .1)
y = step_func(x)
plt.plot(x,y)
plt.ylim(-0.1, 1.1) # y轴范围
plt.title('step function')
plt.show()
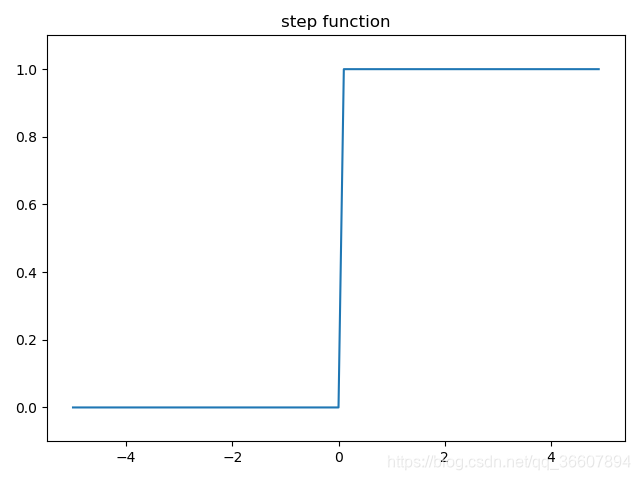
显然,阶跃函数的导数在绝大多数地方(除了0之外)的导数都是0。所以用它做激活函数的话,参数们的微小变化所引起的输出的变化就会直接被阶跃函数抹杀掉,在输出端完全体现不出来,训练时使用的损失函数的值就不会有任何变化,这是不利于训练过程的参数更新的。
(2)sigmoid
h
(
x
)
=
1
1
+
e
x
p
(
−
x
)
h(x)=\frac{1}{1+exp(-x)}
h
(
x
)
=
1
+
e
x
p
(
−
x
)
1
import numpy as np
import matplotlib.pylab as plt
def step_func(x): # 参数x可以接受numpy数组
y = x > 0 # y是布尔型数组
return y.astype(np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5., 5., .1)
y1 = step_func(x)
y2 = sigmoid(x)
plt.plot(x,y1,linestyle='--',color='black')
plt.plot(x,y2,color='black')
plt.ylim(-0.1, 1.1) # y轴范围
plt.title('step function & sigmoid function')
plt.show()

step function 和sigmoid的相同点:
- 都是非线性函数
- 虽然平滑性不同,但宏观上看的形状是相似的,均为“输入小则输出接近0,输入大则输出接近1”
- 输出均在0和1之间
step function 和sigmoid的不同点:
- 导数
sigmoid函数的导数在任何地方都不为0。
而阶跃函数的导数在绝大多数地方(除了0之外)的导数都是0。
sigmoid函数的导数在任何地方都不为0。这对NN的学习非常重要。参数们的一点微小的变化也会引起输出的微小的连续的变化,从而使得损失函数可以连续地变化,从而使得参数的更新正常进行,使得NN的学习正确进行。
所以用它做激活函数的话,参数们的微小变化所引起的输出的变化就会直接被阶跃函数抹杀掉,在输出端完全体现不出来,训练时使用的损失函数的值就不会有任何变化,这是不利于训练过程的参数更新的。
-
平滑性不同。sigmoid是平滑曲线,输出随输入连续变化。而阶跃函数的输出随着输入急剧性变化。
sigmoid的这种平滑性对于NN的学习具有重要意义。
- 阶跃函数只能返回0或1,而sigmoid可以返回0,1之间的实值。所以感知机中流动的是0,1二元信号,而NN中流动的是连续的实值信号。
(3)RELU(Rectified Linear Unit)
NN的历史上,sigmoid最早被使用。但relu最近用的更多。
h
(
x
)
=
{
x
,
x
>
0
0
,
x
≤
0
h(x)=\left\{ \begin{aligned} x,x>0\\ 0,x\leq0 \end{aligned} \right.
h
(
x
)
=
{
x
,
x
>
0
0
,
x
≤
0
def relu(x):
return np.maximum(0,x)
x = np.arange(-5., 5., .1)
y3 = relu(x)
plt.plot(x,y3,color='black')
plt.ylim(-0.1, 5) # y轴范围
plt.title('relu')
plt.show()

输出层
的激活函数
(4)恒等函数(用于回归任务)
机器学习任务通常分为回归和分类两种任务。回归任务是要求出具体的预测值,所以输出层不再使用激活函数进行非线性转换,或者说使用恒等函数作为激活函数,它什么都没做。
def identity_function(x): # 恒等函数,用作回归任务的输出层的激活函数
return x
(5)softmax(用于分类任务)
分类的类别数目等于输出层神经元的数目。
假设输出层有n个神经元,第k个的输出
y
k
y_k
y
k
:
y
k
=
e
x
p
(
a
k
)
∑
i
=
1
n
e
x
p
(
a
i
)
y_k=\frac{exp(a_k)}{\sum_{i=1}^nexp(a_i)}
y
k
=
∑
i
=
1
n
e
x
p
(
a
i
)
e
x
p
(
a
k
)
分母是所有输入信号的指数函数的和,所以输出层的每个神经元都要受到所有输入信号的影响。
重要性质:
∑
k
=
1
n
y
k
=
1
\sum_{k=1}^ny_k=1
∑
k
=
1
n
y
k
=
1
. 这使得我们可以把softmax的输出解释为概率。
e: 纳皮尔常数 2.7182···
'''
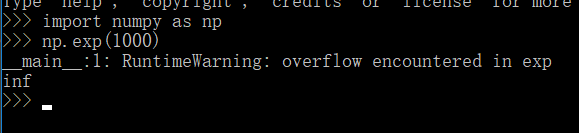
# 这个实现虽然功能正确,但容易导致溢出
# 指数函数的运算容易出现很大的超出数值范围(4或8字节)的数字,如exp(1000)导致溢出overflow
# 推导发现,可以通过减去输入信号的最大值避免溢出,且结果不变
def softmax(a): # a是数组,包含所有的输入信号
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
'''
y
k
=
e
x
p
(
a
k
)
∑
i
=
1
n
e
x
p
(
a
i
)
=
C
e
x
p
(
a
k
)
C
∑
i
=
1
n
e
x
p
(
a
i
)
y_k=\frac{exp(a_k)}{\sum_{i=1}^nexp(a_i)}=\frac{Cexp(a_k)}{C\sum_{i=1}^nexp(a_i)}
y
k
=
∑
i
=
1
n
e
x
p
(
a
i
)
e
x
p
(
a
k
)
=
C
∑
i
=
1
n
e
x
p
(
a
i
)
C
e
x
p
(
a
k
)
=
e
x
p
(
a
k
+
l
o
g
C
)
∑
i
=
1
n
e
x
p
(
a
i
+
l
o
g
C
)
=
e
x
p
(
a
k
+
C
′
)
∑
i
=
1
n
e
x
p
(
a
i
+
C
′
)
=\frac{exp(a_k+logC)}{\sum_{i=1}^nexp(a_i+logC)}=\frac{exp(a_k+C')}{\sum_{i=1}^nexp(a_i+C')}
=
∑
i
=
1
n
e
x
p
(
a
i
+
l
o
g
C
)
e
x
p
(
a
k
+
l
o
g
C
)
=
∑
i
=
1
n
e
x
p
(
a
i
+
C
′
)
e
x
p
(
a
k
+
C
′
)
取
C
′
C'
C
′
为输入信号的最大值,即可解决溢出问题
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c) # 防溢出
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y